omentariosapplet>
We have already studied the "Ellipsograph" or "Trammel of Archimedes" and we know that every point on the moving rod traces an ellipse.

An Ellipsograph is a mechanical device used for drawing ellipses.
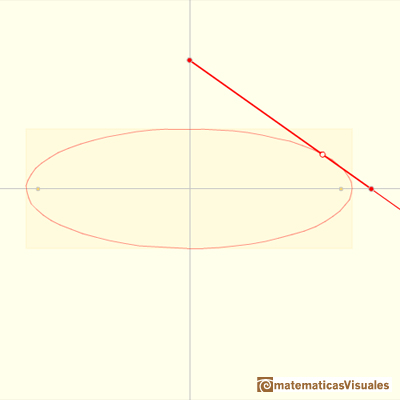
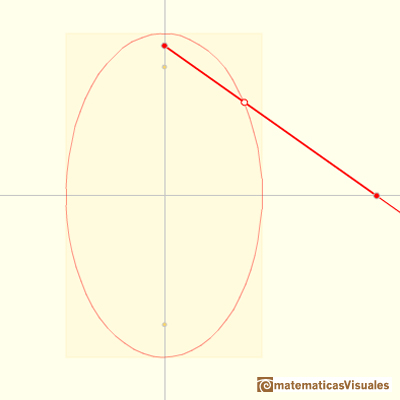
In this page we are going to think only in a line segment of fixed length whose ends slide along two perpendicular axes.
You can imagine that this segment is an sliding ladder.
Following Apostol and Mnatsakanian we will see another proof that every point in the segment draws an ellipse.
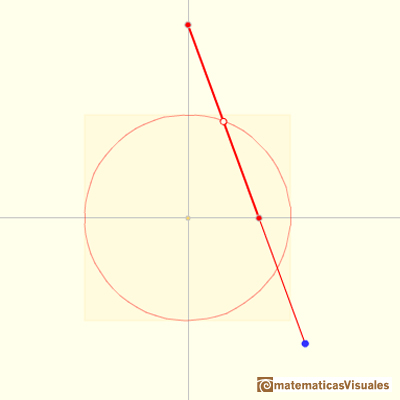
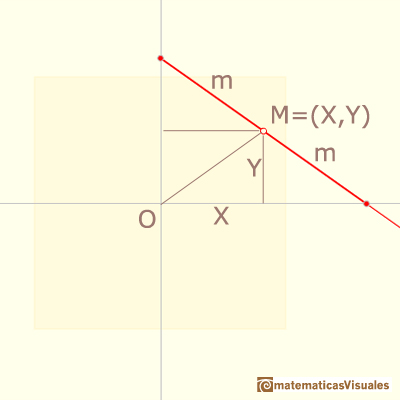
We can start with the simplest case: the midpoint M of the segment traces a circle:
Consider the coordinates of midpoint M of a segment of length 2m
OM and the two perpendiculars from M to each axis divide the large right triangle into four congruent smaller
right triangles, then:
The moving midpoint M always lies on a circle with center O and radius m.
The coordinates of M verify:
This is the Cartesian equation of a circle.
We can write this equation to notice that the circle is a special case of an ellipse:
We are going to use this equation later.
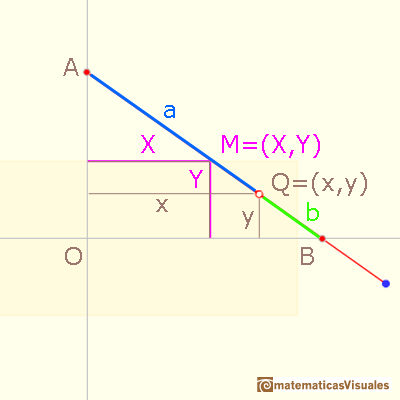
Now we consider a different point Q on the segment
Q divides the trammel into segments of lengths a and b.
Using similar triangles we can relate the coordinates of Q and of the midpoint M:
Using the cartesian formula of the circle as an special case of the ellipse
we have prove that the coordinates of Q
verify equation
and then Q lies on an ellipse.
The same analysis holds if Q is any point on the segment (even if Q is in the line, outside the segment).
In all cases:
The semiaxes of the ellipse are the distances from Q to the endpoints of the segment.
REFERENCES
Tom Apostol and Mamikon Mnatsakanian, 'New Horizons in Geometry' (Chapter 9. Trammels, ), Mathematical Association of America, 2012.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Hilbert and Cohn-Vossen, Geometry and the Imagination. Chelsea Publishing Company. pag.278.
Robert C. Yates, 'A Handbook on curves and their properties', J.W.Edwards-Ann Arbor, 1947.
J.L. Coolidge, The Mathematics of great Amateurs. Second Edition. Claredon Press. Oxford. Jan de Witt's proof in page 124.
MORE LINKS
The Astroid is a particular case of a family of curves called hypocycloids.
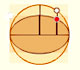
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.
Plane net of pyramids cut by an oblique plane.

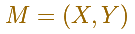
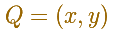
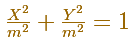
 NEXT
NEXT




















 PREVIOUS
PREVIOUS





