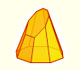
|
|
|
Cylinders cut by an oblique plane
The solid cut from an infinite circular cylinder by two planes is a cylindrical segment or a truncated cylinder. The simplest case is when one of the cutting planes is perpendicular to the axis of the cylinder. Then the cylindrical segment has a circular base.
The main interest of this page is to see how a truncated cylinder can be developed into a plane.
This in another example:
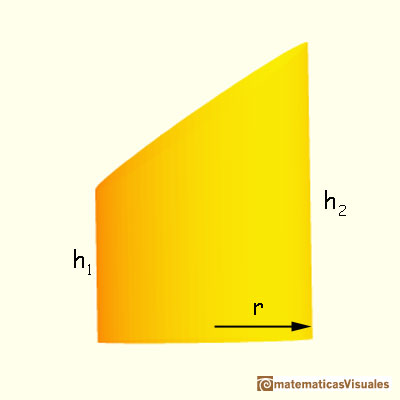
The volume of a cylindrical segment it is easy to obtain if we notice that two copies of the cylindrical segment one of them turned upside-down, together form a cylinder.
The section of a cylinder by an oblique plane looks like an ellipse. This is true and a beautiful demonstration uses Dandelin Spheres.
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.
REFERENCES
Hilbert and Cohn-Vossen. Geometry and the Imagination. Chelsea Publishing Company. pag.7.
NEXT
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
PREVIOUS
We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
MORE LINKS
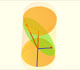
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.
Plane net of pyramids cut by an oblique plane.
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
Plane developments of cones cut by an oblique plane. The section is an ellipse.
Durer was the first who published in german a method to draw ellipses as cone sections.
Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
Plane nets of prisms with a regular base with different side number cut by an oblique plane.
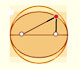
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
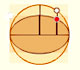
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
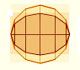
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
Using Cavalieri's Principle we can calculate the volume of a sphere.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.