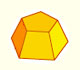
A regular octahedron is a polyhedron with eight equilateral triangular faces, six vertices and twelve edges.
It is a Platonic solid well known from Antiquity.

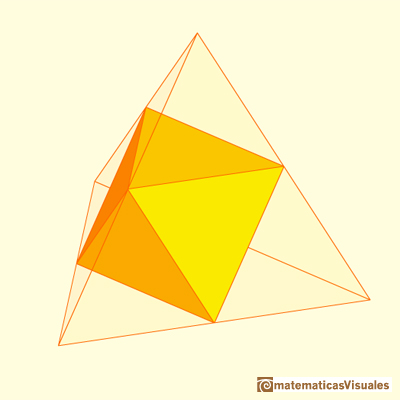
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
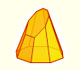
Leonardo da Vinci drew two octahedra for Luca Pacioli's book 'De Divina Proportione' (published in 1509).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.
It was Durer the first to publish plane nets of polyhedra. In his
book 'Underweysung der Messung' ('Four Books of Measurement', published in 1525) the author draw plane developments of several
Platonic and Archimedean solids, for example, this regular tetrahedron:
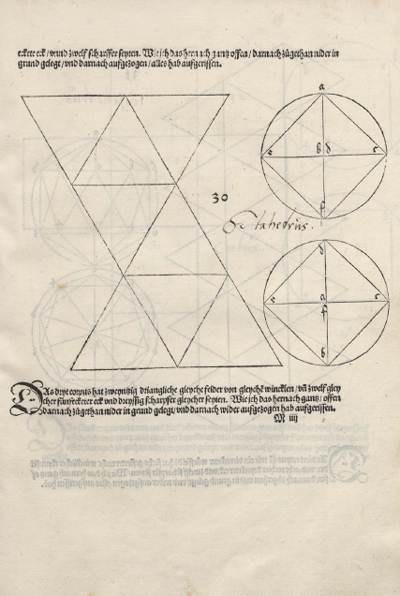
"Whether or not Dürer was acquainted with the work of the two Italian specialists in this fiel, Luca Pacioli
and Piero della Francesca, is an open question. Certain it is that (...) he tackled the problem in an entirely independent way. Pacioli
(...) illustrates them [several polyhedra] in perspective or stereographic images. Dürer treats (...)[more polyhedra] and instead of
representing the solids in perspective or stereographic images, he devised the apparently original and, if one may say so,
proto-topological method of developing them on the plane surface in such a way that the facets form a coherent 'net' which,
when cut out of paper and properly folded where two facets adjoin, will form an actual, three-dimensional model of the solid
in question." (Panofsky, p.259)
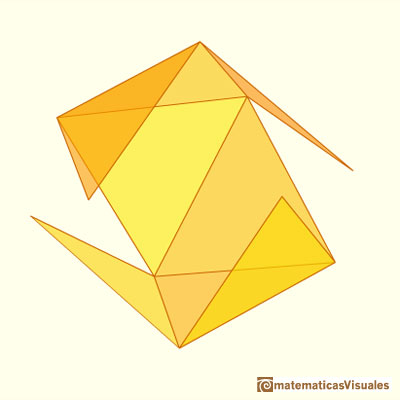
Playing with the application you can see how an octahedron develops into a plane net.
You can download the plane net of this octahedron and build your own.
INVESTIGATE
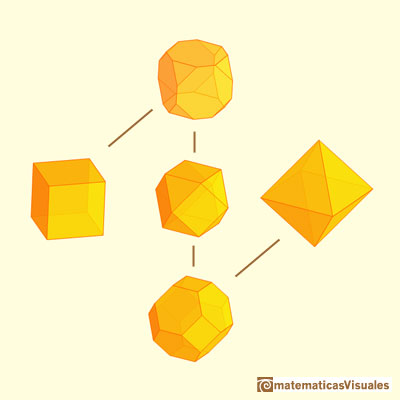
Some relations between the octahedron and other polyhedra:
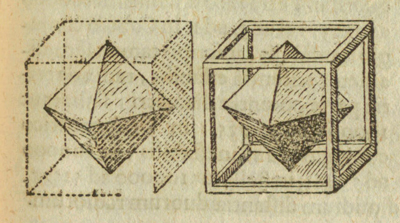
Octahedra and cubes are dual polyhedra:
Kepler's drawing of an octahedron inside a cube:
Cube and octahedron in reciprocal position (Stellation of a cuboctahedron)

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
Stella Octangula is the name that Kepler used to one stellation of an octahedron:

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
The truncated octahedron is an Archimedean solid that has very interesting properties:
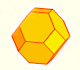
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
We can get an octahedron truncating a tetrahedron:
REFERENCES
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Erwin Panofsky - The Life and Art of Albrecht Dürer - Princeton University Press
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press (p. 76)
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MORE LINKS

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using cardboard you can draw plane nets and build polyhedra.

A very simple technique to build complex and colorful polyhedra.

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

Examples of polyhedra built using tensegrity.

Material for a session about polyhedra (Zaragoza, 13th Abril 2012).

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.

Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.

Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.

Examples of polyhedra built using Zome.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane net of pyramids cut by an oblique plane.

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.




















 NEXT
NEXT
 PREVIOUS
PREVIOUS