|
|
Llenando el espacio con dodecaedros rómbicos
Taller de Talento Matemático de Aragón
I.E.S. Alonso Quijano de Alcalá de Henares
Día Internacional de las Matemáticas 2024
Para celebrar el Día Internacional de las Matemáticas 2024 el
Taller de Talento Matemático de Aragón
organizó la actividad 'Llenando el espacio con dodecaedros rómbicos'.
Se realizó el viernes 8 de marzo a las 18:00 en Etopia Centro de Arte y Tecnología, situado en la Avenida Ciudad de Soria, 8 de Zaragoza.
Diseño: Miguel Cardil
Puedes
descargar el cartel aquí.
Con el mismo espíritu que la actividad que realizamos el año 2023, hemos construido entre todos los participantes
una escultura matemática multicolor que se ha expuesto en
Etopia Centro de Arte y Tecnología. Después se trasladará al vestíbulo de la
Facultad de Ciencias (edificio de Matemáticas).
Participaron más de cien chicos y chicas y este es un resumen fotográfico de la actividad:
Fue una actividad del Taller de Talento Matemático abierta a todo el mundo.
En particular, estuvieron invitados los chicos y chicas de Secundaria y Bachillerato, padres y madres, profesores y
todos los que quiesieron colaborar y pasar un buen rato con esta actividad artística y matemática.
Los participantes necesitaron tijera, regla y pegamento.
Un pegamento ideal para este tipo de construcciones es el pegamento transparente de tubo, tipo Imedio-UHU.
El taller 'Llenando el espacio con dodecaedros rómbicos' también se realizó en el IES Alonso Quijano
de Alcalá de Henares el 14 de marzo de 2024.
Diseño: Miguel Cardil
Puedes
descargar el cartel de la actividad del IES Alonso Quijano aquí.
Participaron unos 400 alumnos del IES Alonso Quijano.
Con la escultura se ha realizado una exposición que estará en el instituto unos meses.
Estas son algunas imágenes de la exposición:
En marzo de 2023, la escultura que realizamos tenía como módulo
base al octaedro truncado. Puedes ver más información sobre esa actividad en el siguiente enlace:

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
Este año utilizamos otro poliedro que rellena el espacio: el dodecaedro rómbico. En la construcción mostramos también la
relación de este poliedro con los panales de las abejas.
La escultura matemática está formada por módulos que hicimos con cartulina.
El módulo principal que utilizamos es el dodecaedro rómbico. También contruimos un panal de abejas:
En la charla hablamos de estos poliedros, presentamos modelos
realizados con diferentes técnicas y practicamos un poco construyendo dodecaedros rómbicos.
Con todos esos poliedros construimos una gran escultura matemática.
Lo que sigue son unas notas de ampliación.

1.- El tetraedro
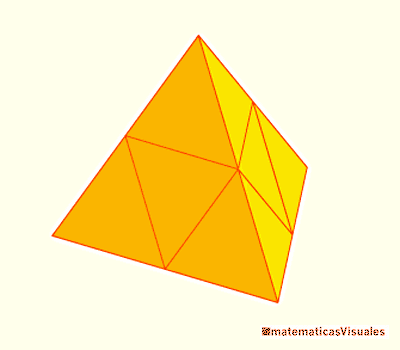
El Tetraedro es el sólido platónico más sencillo. Conocido desde épocas muy remotas.
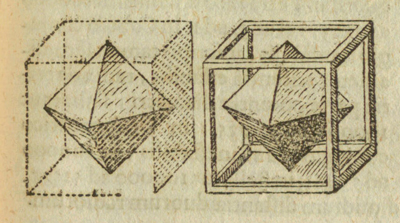
Es descrito por Luca Pacioli en su libro 'La Divina Proporción' donde podemos ver una ilustración de Leonardo da Vinci.
El tetraedro es una pirámide y su volumen es un tercio del área de la base por la altura. Así podemos calcular su
volumen pero vamos a ver una construcción (que ya nos enseñó Kepler) que nos va a facilitar la tarea.
Se puede construir un tetraedro dentro de un cubo:
PARA PENSAR UN POCO
A partir de esta construcción podemos calcular el volumen de un tetraedro de arista 1:

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

2.- Octaedro
Podemos pensar que el octaedro está formado por dos pirámides de base cuadrada unidas. Su desarrollo es fácil de
construir pues sus caras son triángulos equiláteros.
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales
dos a dos que contienen las 12 aristas y los 6 vértices del
octaedro regular.
PARA PENSAR UN POCO
A partir de esta construcción podemos calcular el volumen de un octaedro (y este es un ejemplo bien claro de que si se tiene en la mano
este modelo el razonamiento se entiende mucho mejor):

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

3.- Dualidad
En una breve historia de los poliedros tendríamos que citar, por lo menos, a Platón, Euclides, Arquímedes, Pacioli, Durero, Kepler.
Un cambio crucial en cómo vemos los poliedros lo asociamos a Euler. Euler considera que un poliedro está formado por vértices
(elementos de dimensión 0), aristas (dimensión 1) y caras (dimensión 2).
Entonces deduce la famosa Fórmula de Euler:
Una consecuencia de este punto de vista es que podemos considerar ciertas deformaciones del poliedro y la fórmula se sigue verificando pues
lo importante no es que las aristas sean rectas o que tengan tales o cuales medidas. Podemos imaginar la figura hecha de goma y estirando
(sin rasgar) deformamos el poliedro pero la fórmula se seguirá cumpliendo. Estas ideas
(junto con el problema de los Puentes de Koningsberg -que resolvió Euler-) están en el origen de una rama de las Matemáticas que llamamos
Topología.
INVESTIGA
Contar los vértices, aristas y caras de los sólidos platónicos y comprobar que se cumple la Fórmula de Euler.
Tetraedro:
Cubo:
Octaedro:
Icosaedro:
Dodecaedro:
Nosotros nos vamos a quedar en una consecuencia sencilla de ese énfasis en vértices, aristas y caras.
A partir de un poliedro vamos a pensar en otro poliedro que tenga las mismas aristas pero que intercambie el número de vértices con el de caras.
A este nuevo poliedro lo llamaremos el dual del poliedro inicial. Si hacemos 'el dual del dual' volvemos al poliedro inicial.
Es decir, los poliedros se pueden emparejar en parejas de poliedros duales.
INVESTIGA
¿Cúales son los duales de los cinco sólidos platónicos?
Vamos a ver dos maneras de colocar una pareja de poliedros duales. La primera es pensando en que el dual de un poliedro tiene tantos vértices como
caras tiene su dual. Vamos a marcar un punto en cada cara de un poliedro (si la cara es un polígono regular, podemos marcar el circuncentro). Uniendo
estos vértices obtenemos el poliedro dual.
Hacemos esta construcción para el caso del tetraedro (y su dual, otro tetraedro), con origami:
La misma construcción usando una combinación de tubos y tensegrity:
PARA PENSAR UN POCO
¿Cuál es el tamaño relativo de estos dos tetraedros?

4.- El cubo y su dual, el octaedro
Sabemos poner un tetraedro dentro de un cubo y poner un octaedro dentro de un tetraedro.
Construyendo los tres poliedros obtenemos un octaedro con sus vértices en el centro de las caras del cubo.
El cubo y el octaedro son poliedros duales.
Así lo vio Kepler:
PARA PENSAR UN POCO
La siguiente fotografía es un dado, con sus seis números, pero que no es un cubo, es una esfera.
Sin embargo 'funciona' como si fuera un dado normal. Dentro está hueco y hay una bolita.
¿Te puedes imaginar que forma tiene el hueco en el que está la bolita?
INVESTIGA
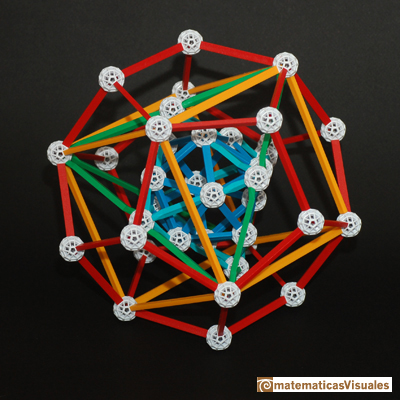
Si te fijas, en la fotografía de los poliedros con tubos se pueden ver cuatro poliedros. ¿Se pueden construir los cinco sólidos platónicos,
uno dentro de otro?
Este es un modelo de Zome:
Vamos a ver ahora cómo a partir de un poliedro podemos construir otros poliedros.

5.- Añadiendo pirámides
Una manera de construir nuevos poliedros es añadir pirámides a las caras de otro poliedro.
Este procedimiento es descrito por Luca Pacioli. A estos poliedros los llama 'elevatus'. Esta es una ilustración de Leonardo da Vinci:
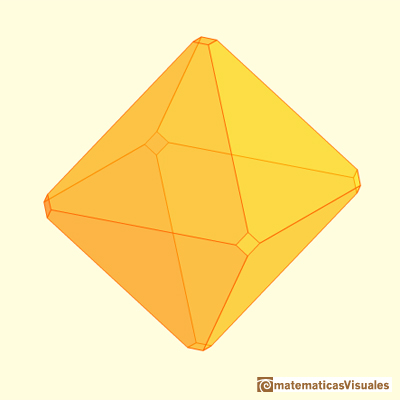
Un ejemplo interesante es partir de un octaedro y añadirle cuatro tetraedros:
PARA PENSAR UN POCO

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
¿Qué relación hay entre el volumen del octaedro y el del tetraedro?
Por lo tanto, el volumen del tetraedro es:

6.- El octaedro estrellado o stella octangula
En la construcción anterior sólo hemos puesto tetraedro en cuatro caras del octaedro. Si ponemos un tetraedro
en cada cara obtenemos un poliedro ya descrito por Pacioli y dibujado por Leonardo.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).
Kepler se volvió a fijar en este poliedro y lo llamó Stella Octangula. Lo hizo desde otro punto de vista muy interesante.
No piensa en que se añaden pirámides a las caras sino en que se plogonga el plano de cada cara del octaedro. Esos planos
se cortan y delimitan un nuevo poliedro.
A estos poliedros los llamamos estrellados. La Stella Octangula es el octaedro estrellado.
PARA PENSAR UN POCO

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
¿Cuál es el volumen del octaedro estrellado o Stella Octangula de arista a?
INVESTIGA
Kepler describió más poliedros estrellados, por ejemplo este gran dodecaedro. Investiga sobre los poliedros llamados de
Kepler-Poinsot.
Otra manera de ver el octaedro estrellado es pensar que es un poliedro compuesto por dos poliedros: un tetraedro y su dual, otro tetraedro.
Esto nos va a llevar a la segunda manera de colocar dos poliedros duales. Vamos a fijarnos en esta construcción.
Dos poliedros duales tienen el mismo número de aristas. Si son poliedros regulares (como es el caso de los tetraedros) podemos
colocar las aristas de modo que se bisequen y se corten ortogonalmente.
Entonces:
1) Obtenemos un nuevo poliedro compuesto.
2) Hay una parte común a ambos poliedros, en este caso, es el octaedro.
3) El poliedro compuesto es una estelación de esa parte común: el octaedro estrellado.
4) Los vértices del poliedro compuesto determinan un poliedro 'exterior' que contiene al poliedro compuesto: La Stella octangula
está contenida en un cubo.
5) El poliedro 'común' y el 'exterior' son poliedros duales.
Vamos a ver qué ocurre si colocamos en esta posición otros dos poliedros duales, el cubo y el octaedro.

7.- Cubo y su dual el octaedro en posición recíproca
Si consideramos un cubo y un octaedro y los colocamos en 'posición recíproca' de modo que pares de aristas se bisequen
ortogonalmente:
1) Obtenemos un poliedro compuesto:
2) El poliedro 'común' tiene caras que son cuadrados y triángulos equiláteros. Se llama cuboctaedro.
3) El poliedro compuesto es una estelación de éste: cuboctaedro estrellado.
4) Los vértices del cuboctaedro estrellado determinan un nuevo poliedro que es el dodecaedro rómbico.
5) El cuboctaedro y el dodecaedro rómbico son poliedros duales.
PARA PENSAR UN POCO

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
¿Puede calcular el tamaño relativo de estos poliedros?
Vamos a ver algunas propiedades del cuboctaedro y del dodecaedro rómbico.

8.- El cuboctaedro
El cuboctaedro es un poliedro que tiene caras que son cuadrados y triángulos equiláteros.
Descrito por Luca Pacioli y dibujado por Leonardo da Vinci

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
Es un sólido arquimedianos. Algunos de estos poliedros son descritos en el libro de Pacioli 'La Divina Proporción'
pero fuero descritos sistemáticamente por Kepler.
INVESTIGA
Buscar descripciones de los trece sólidos arquimedianos.
Ilustraciones del libro de Kepler 'Harmonices Mundi':
A partir de un poliedro podemos obtener otros poliedros cortando vértices. Este proceso se llama truncamiento.
Algunos de los sólidos arquimedianos se obtienen por truncamiento y el cuboctaedro se puede conseguir truncando un cubo
o truncando un octaedro.
Empezamos truncando un cubo:
Obtenemos un sólido arquimediano (cubo truncado) con caras que son triángulos equilátero y octógonos:
Llegamos al cuboctaedro:
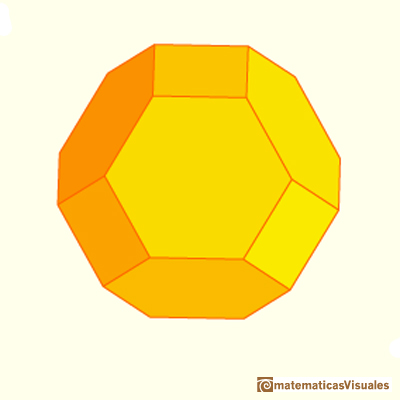
Desde allí podemos ir hacia el octaedro y obtener otro sólido arquimediano, el octaedro truncado:
PARA PENSAR UN POCO

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
Podemos calcular el volumen del cuboctaedro viéndolo como un cubo truncado o un octaedro truncado.
El volumen del cuboctaedro de arista 1 es:
Si pensamos que este cubo está formado por ocho cubos más pequeños (que tienen en común el vértice en el centro del cubo grande)
podemos ver que la distancia desde el centro del cuboctaedro (su centro de gravedad) hasta cualquier vértice es la longitud de la arista
(pues es igual a la diagonal de una cara de un cubo de los pequeños).
Los vértices de este bonito modelo de origami modular, la Omega Star, son los vértices de un cuboctaedro:
INVESTIGA
El octaedro truncado tiene la interesante propiedad de teselar el espacio (al igual que el poliedro que vamos a
estudiar a continuación, el dodecaedro rómbico). Investiga propiedades del octaedro truncado que puedan justificar
esta propiedad de teselar el espacio.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

9.- Dodecaedro rómbico
Ya hemos visto cómo se obtiene el dodecaedro rómbico a partir del cuboctaedro estrellado.
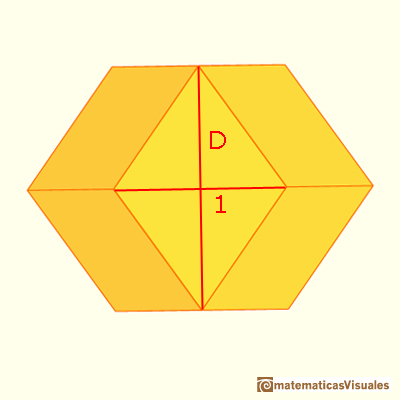
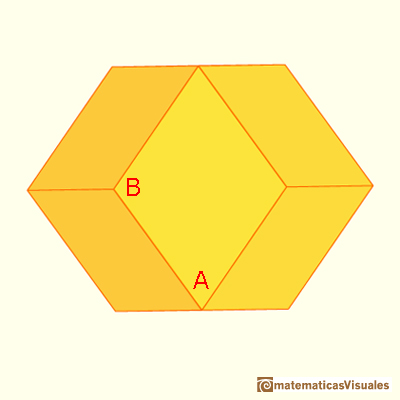
Está formado por doce rombos y sabemos la relación entre sus diagonales.
Si la diagonal pequeña mide 1 la diagonal grande es:
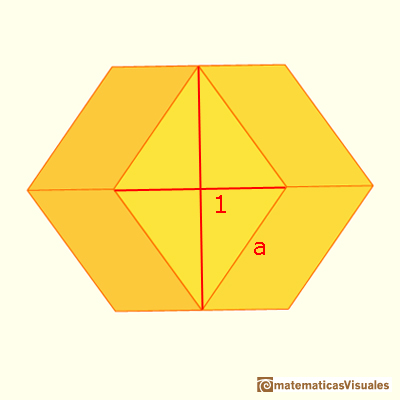
Y el lado del dodecaedro rómbico mide:
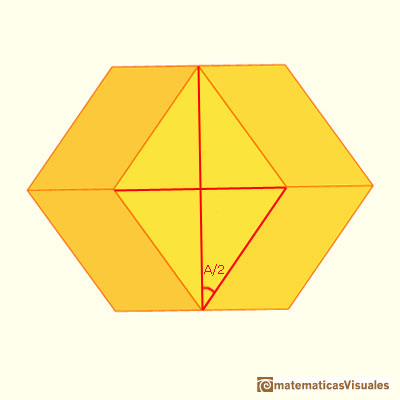
Usando trigonometría también podemos medir los ángulos del rombo que son:
Comprobamos que el dodecaedro rómbico y el cuboctaedro son sólidos duales. Los duales de los sólidos arquimedianos
se llaman sólidos de Catalán. El dodecaedro rómbico es un sólido de Catalán.
Contamos las caras, aristas y vértices del cuboctaedro:
Y los elementos del dodecaedro rómbico:
En las siguientes construcciones con Zome se puede ver la dualidad entre el dodecaedro rómbico (amarillo)
y el cuboctaedro (verde).
Hay muchas construcciones del dodecaedro rómbico con diferentes técnicas. Una especialmente curiosa esta hecha con cartas dobladas
(¡las cartas no están pegadas, se sostienen unas a otras!) y que he aprendido de George Hart.
Con origami modular se puede hacer un dodecaedro rómbico. A estas alturas no nos extraña que se necesiten 12 piezas de papel, pero que no se parte de cuadrados (como es
bastante habitual): las hojitas tienen que tener una proporción como la de los folios de papel que usamos con el estándar DIN A.
INVESTIGA

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
Para obtener el cuboctaedro y el dodecaedro rómbico hemos colocado dos poliedros duales (el cubo y el octaedro) es
'posición recíproca'.
Investiga si se puede hacer esto mismo con los otros dos poliedros platónicos duales, el dodecaedro y el icosaedro.
¿Que poliedros 'común' y 'exterior' se obtienen?
¿Son dos poliedros duales?
¿Resulta ser el poliedro 'común' un sólido arquimediano?

10.- Dodecaedro rómbico: achaflanando un cubo
Otro modo de obtener nuevos poliedros a partir de otros es achaflanando las aristas.
Por ejemplo, en el caso del cubo:
Si achaflanamos más y más obtenemos un dodecaedro rómbico.

11.- Dodecaedro rómbico: un cubo con pirámides
Otro modo de ver el dodecaedro rómbico es como un cubo al que se añaden una pirámide en cada cara. Obtenemos un poliedro
con 24 caras.
Para una determinada altura, dos caras adyacentes de dos pirámides quedan en el mismo plano. Este poliedro tiene doce
caras y es el dodecaedro rómbico.
Obtenemos varias consecuencias de esta construcción. La primera es que es muy sencillo calcular el volumen del
dodecaedro rómbico pues es el doble del cubo que está contenido en él.
La segunda es que el cubo y el dodecaedro son 'reversibles'
Este es un modelo hecho con cartulina. Puedes ver la técnica de construcción (en el interior hay unos imanes):
La tercera consecuencia la comentamos en el siguiente apartado

12.- Con dodecaedros rómbicos llenamos el espacio
Como una consecuencia de la construcción anterior podemos rellenar el espacio con dodecaedros rómbicos.
Así lo explica Steinhaus: "Hemos comentado la posibilidad de llenar con cubos la totalidad del espacio.
También lo conseguiremos merced al procedimiento siguiente: colocamos cubos alernativamente blancos y negros, a
modo de damero tridimensional, luego retiramos los cubos negros. Descomponemos cada uno de los huecos en seis
pirámides de bases cuadradas, con vértice en el centro del hueco cúbico. Si nos fijamos en sólo uno de los cubos
blancos, provisto de 6 pirámides con bases en él, veremos un dodecaedro rómbico con un cubo inscrito en su interior:
por la definición de nuestro procedimiento, es obvio que habremos llenado la totalidad del espacio con
dodecaedros rómbicos congruentes." (Steinhaus, p. 186)
Decimos que el dodecaedro rómbico es un poliedro que tesela el espacio (también lo hace el cubo y el octaedro truncado, entre otros)
Construcciones con Zome que muestran cómo el dodecaedro rómbico tesela el espacio:

13.- El dodecaedro rómbico y los panales
El dodecaedro rómbico aparece en la naturaleza. Por ejemplo en los cristales de granate.
El que primero describe en una publicación este poliedro fue Kepler, aunque era conocido con anterioridad. Kepler también se dio cuenta de que las abejas cierran sus
celdillas hexagonales con tres rombos e intuyó que esos rombos eran los del dodecaedro.
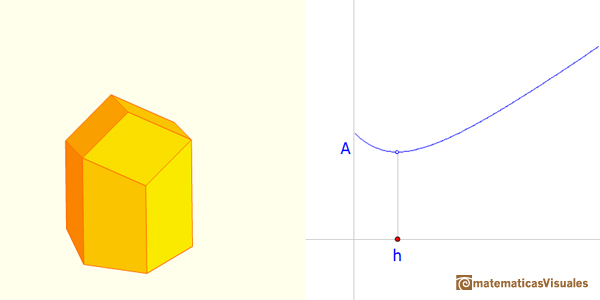
Se puede demostrar que si queremos cerrar un prisma hexagonal con tres rombos el modo más económico, el que utiliza menos cera,
es usando tres rombos del dodecaedro rómbico. Para ello necesitamos un poco de cálculo diferencial.

14.- Construcción de un dodecaedro rómbico
Vamos a construir un modelo en cartulina. Hay dos variantes que son dos cajas. Una con forma de dodecaedro rómbico y la
otra es una celda de panal de abeja. Cuando tengamos muchos modelos podremos encajar unos con otros y ver cómo teselan el
espacio.
El diseño fue ideado por John Edminster y se pueden encontrar referencias en
Beach Packaging Design.
Se puede ver cómo cabe un octaedro dentro del dodecaedro y también un cubo. Dentro del cubo se puede poner un cubococtaedro
(en este caso, una estrella omega hecha con papiroflexia):
Estos son los modelos que se pueden descargar:
Un octaedro que se puede incluir en el dodecaedro rómbico:
Un cubo que se puede incluir en el dodecaedro rómbico. Con seis cuadrados se puede hacer una Omega Star de papiroflexia (que es un cuboctaedro) que cabe dentro del cubo:
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Luca Pacioli - De divina proportione - (La divina proporción) Ediciones Akal, 4ª edición, 2004. Traducción al castellano de Juan Calatrava.
 SIGUIENTE SIGUIENTE

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
 ANTERIOR ANTERIOR

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.
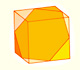
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
Desarrollos planos de pirámides truncadas por un plano oblicuo.
|

































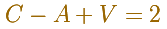







































































 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR



























