|
|
El icosaedro
Taller de Talento Matemático (Zaragoza)
Sesión del Taller de Talento Matemático de Aragón por Roberto Cardil.
Programada para el viernes 12 de Noviembre de 2021 a las 18:15 en la Facultad de Matemáticas de la Universidad de Zaragoza.
Es necesaria inscripción debido a COVID.
Enhorabuena al Taller de Talento Matemático por poder reanudar la actividad.
Será una sesión semejante a la que se realizó el 19 de Octubre de 2018 con nuevos poliedros.
En esta sesión tenemos dos objetivos:
OBJETIVO 1
Queremos pasar un rato hablando de poliedros. Este año estudiaremos un poliedro muy bonito que se llama icosaedro.
Veremos cómo diferentes construcciones nos ayudan a pensar sobre algunas propiedades de este poliedro.
OBJETIVO 2
El objetivo principal es construir alguna figura geométrica y
animar a la construcción de poliedros con diferentes técnicas sencillas (papiroflexia, cartulina, tubos, gomas, Zome, etc.).
Queremos construir poliedros para disfrutar de su belleza, mejorar nuestra percepción espacial y obtener conclusiones matemáticas.
Construir y manipular poliedros nos permiten comprenderlos mejor.
La mayor parte del tiempo la dedicaremos a hacer una construcción.
IMPORTANTE: Necesitaremos tijera, regla y pegamento.
También papel y lápiz.
La construcción que haremos es un icosaedro (un poco truncado) hecho con discos de cartulina.
Traed algún poliedro que tengáis por casa. Así todos nos animamos a construir figuras geométricas.
Esta sesión tiene un espíritu parecido a las otras sesiones que hemos realizado sobre poliedros
para el Taller de Talento Matemático de Zaragoza:

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
En matemáticasVisuales hay varias páginas dedicadas al icosaedro. Aquí vamos a hacer un resumen y vamos a ver
varias construcciones relacionadas con el icosaedro y lo que nos enseñan sobre este poliedro. Pues el objetivo
principal de esta página es animaros a construir poliedros.

1.- El icosaedro es uno de los cinco sólidos platónicos
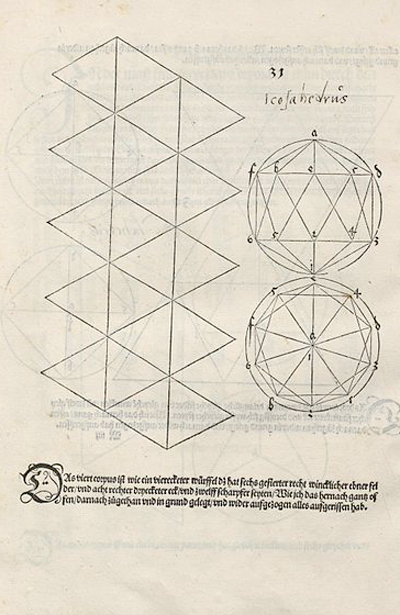
El icosaedro tiene 20 caras que son triángulos equiláteros. Su desarrollo nos lo mostró Durero y es muy fácil de dibujar
y de construir:
Sus caras son iguales y son un polígono regular, en cada vértice concurren el mismo número de aristas
(y también de caras, claro).
Por lo tanto, el icosaedro es un sólido platónico.

Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
Hay otros dos sólidos platónicos formados por triángulos: el tetraedro y el octaedro.
Veremos más adelante que el icosaedro está muy relacionado con el dodecaedro pues son
poliedros duales.

2.- Construcción del icosaedro 'cara a cara': vértices y aristas
La técnica de construir poliedros con cartulina recortando cada cara por separado es muy sencilla y nos permite hacer
poliedros con diferentes colores en sus caras.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
Si pensamos en estas caras por separado contaremos con facilidad los vértices y las aristas del icosaedro sin dejarnos
ninguna.
Necesitamos 20 caras que son triángulos equiláteros.
En total tenemos 20x3 aristas de triángulos. En total 60 que se pegan dos a dos, es decir, el icosaedro tiene 30
aristas.
En cada vértice del icosaedro se juntan 5 vértices de los triángulos.
Tenemos 20x3 vértices de triángulos. En total 60 que se juntan de 5 en 5, por lo tanto, el icosaedro tiene
12 vértices.
Por lo tanto, el número de caras, aristas y vértices de un icosaedro es:

3.- Una variante: construcción con discos de cartulina
Una variante de la técnica de construcción de poliedros con cartulina es usar círculos.
Esos círculos se van pegando hasta formar el poliedro. Usaremos esta técnica en la propuesta de
construcción de este taller.

Técnica simple para construir poliedros pegando discos de cartulina.
Los discos también pueden unirse con gomas elásticas.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
Por ejemplo, esta lámpara icosaédrica hecha con
cartulina y gomas elásticas, muy parecida a la construcción que vamos a hacer:
Con el juego Acona Biconbi de Bruno Munari
se puede construir un icosaedro muy bonito:

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

4.- Construcción con varillas
Si queremos construir el esqueleto de un icosaedro necesitamos 30 varillas para sus aristas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.
Estas varillas pueden ser de aluminio, plástico u otros materiales.
¿Qué podemos aprender con esta construcción? Si se van uniendo con bridas, en principio la estructura no es rígida pero cuando completamos el icosaedro vemos
que resulta una estructura rígida.
Esta propiedad la tienen también el tetraedro y el icosaedro al estar formados por
triángulos. Pero no la tienen el cubo ni el dodecaedro.
Este tipo de estructuras formadas por triángulos son muy útiles en arquitectura e ingeniería.
Otro ejemplo son las cúpulas geodésicas.

5.- El icosaedro y el pentágono: la razón áurea
En cada vértice del icosaedro se unen cinco caras. Si nos fijamos en esas cinco caras se forma una pirámide. La
base es un pentágono regular.
Vamos a ver el interior del icosaedro con este modelo hecho con cartulina. Las diferentes partes se unen con imanes.
Vemos la base pentagonal de la pirámide y una de las diagonales del pentágono regular.
La diagonal de un pentágono y su lado están en proporción áurea.
Para saber más sobre el pentágono y la proporción áurea puedes consultar estos enlaces:

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
Si nos fijamos en una diagonal vemos que alguna arista del icosaedro es perpendicular y que dos diagonales y dos
de esas aristas forman un rectángulo que es un rectángulo áureo.
En el interior del icosaedro hemos encontrado un rectángulo especial, un rectángulo áureo. Este rectángulo contiene
dos aristas del icosaedro y cuatro de sus 12 vértices.

6.- Tres rectángulos áureos contienen los vértices del icosaedro
El icosaedro tiene doce vértices.
Resulta que estos doce vértices son los vértices de tres rectángulos áureos ortogonales dos a dos.
Una construcción preciosa que recomiendo hacer con madera aunque también se puede hacer con cartulina o
cartón pluma. Es fácil de hacer.
En el siguiente enlace puedes aprender más sobre esta construcción tan interesante. Encontrarás también
una plantilla para descargar, recortar y montar el icosaedro.

Con tres rectángulos áureos podemos construir un icosaedro.

7.- Los anillos de Borromeo
Si hacemos la construcción anterior lo veremos muy claro: los tres rectángulos están entrelazados de un modo
especial. Cuando la figura está terminada los rectángulos no se pueden separar pero si cortamos una de las piezas
y la separamos los otros dos rectángulos están sueltos y se separan sin problemas.
Los tres rectángulos están entrelazados formando lo que llamamos los anillos de Borromeo.
Podemos hacer los anillos de Borromeo usando tres globos.
No podemos dejar de comentar esta propiedad de la construcción del icosaedro con tres rectángulos áureos pues la sesión
del Taller del Talento Matemático de Zaragoza
para la que esta página está desarrollada se realiza a escasos metros de una interesante obra.
A la entrada de la Facultad de Matemáticas de la Universidad de Zaragoza hay una escultura homenaje a los anillos de Borromeo:

8.- Tensegridad
Una tensegridad (tensegrity)
es una estructura formada por barras y tensores que mantienen las barras en equilibrio.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
La construcción del icosaedro con tres rectángulos áureos inspira una tensegridad muy sencilla y bonita.
Podemos construir la estructura de un icosaedro usando seis barras y seis gomas elásticas.

9.- El volumen del icosaedro
Calcular el volumen de un icosaedro parece una tarea difícil.
Una vez más una construcción nos ayuda a comprender el problema.
Si nos fijamos en la construcción de los tres rectángulos áureos nos podemos plantear el cortar el icosaedro
en ochos partes y así ver el interior del poliedro y, en particular, su centro.
Luego nos bastará usar una herramienta básica como es la semejanza de triángulos y alguna propiedad de la
proporción áurea para calcular el volumen del icosaedro.
En el siguiente enlace encontrarás una explicación detallada de cómo calcular el volumen de un icosaedro y, además,
una plantilla para construir un octavo de icosaedro.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

10.- Icosaedro inscrito en un octaedro
Los doce vértices de un icosaedro están en tres rectángulos áureos que son ortogonales dos a dos. También los seis vértices
de un octaedro están en tres cuadrados que son ortogonales dos a dos.
Estas dos construcciones combinadas nos ayudan a ver cómo podemos inscribir un icosaedro en un octaedro de modo que los
vértices del icosaedro estén en las aristas del octaedro.
Puedes ver construcciones con varias técnicas (madera y cartón pluma, impresión 3d, cartulina) en el siguiente enlace.
También se explica un segundo método para calcular el volumen del icosaedro.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

11.- El icosaedro y el dodecaedro son poliedros duales
Hemos visto que hay una relación entre el icosaedro y el pentágono. El dodecaedro es el sólido platónico que podemos
hacer con pentágonos. Resulta que entre el icosaedro y el dodecaedro hay una relación muy importante que llamamos dualidad.
Decimos que el icosaedro y el dodecaedro son poliedros duales.
Si quieres aprender o repasar algo más sobre la dualidad aplicada a los sólidos platónicos puedes ver el siguiente
enlace:

Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
El dodecaedro con una proyección del globo terráqueo es una magnífica construcción que he sacado del
sitio web de Furuti sobre construcción de poliedros con proyecciones de mapas.

12.- Otros poliedros relacionados con el icosaedro
Si truncamos un icosaedro obtenemos el icosaedro truncado (claro). Este poliedro es muy conocido pues se
utiliza para fabricar los balones de muchos deportes. Pero también está relacionado con la estructura
molecular del Carbono-60.
Si profundizamos más en el truncamiento obtenemos el icosidodecaedro (que está relacionado tanto con
el icosaedro como con el dodecaedro). El icosidodecaedro es un sólido arquimediano.
Este icosidodecaedro se le deja a un gato para que aprenda Geometría:
El poliedro dual del icosidodecaedro es un sólido de Catalán que se llama triacontaedro:
El siguiente poliedro es el rombicosidodecaedro grande, también llamado icosidodecaedro truncado (si truncamos un icosidodecaedro
obtenemos un sólido muy parecido a este pero que tiene rectángulos en vez de cuadrados). El rombicosidodecaedro grande es un
sólido arquimediano.
Otro sólido arquimediano relacionado con el icosaedro es el rombicosidodecaedro:
Los nodos que usa Zome son una variante de rombicosidodecaedro (los cuadrados son sustituidos por
rectángulos áureos):
INVESTIGA
Otra familia de poliedros es la de Kepler-Poinsot.
Un ejemplo es este gran icosaedro
(construido según el desarrollo de Korthalsaltes):

13.- Construcción del icosaedro
Vamos a construir un icosaedro (ligeramente truncado) usando 20 discos de cartulina.
Queda muy bien usando cinco colores distintos. Un reto es conseguir que no haya dos caras contiguas del mismo color.
El resultado será:
Hemos usado esta técnica de los discos en otras ocasiones:

Técnica simple para construir poliedros pegando discos de cartulina.
Podríamos usar la siguiente plantilla y recortar los 20 discos:
Para que podamos hacer la figura rápido he recortado muchos discos con una troqueladora:
Podemos preparar unas plantillas que nos ayuden a marcar los dobleces:
Así marcaremos los dobleces con la ayuda de una tijera y una regla:
Sólo falta doblar y pegar.
Se puede descargar un documento con las plantillas que hemos usado:
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE SIGUIENTE

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.
 ANTERIOR ANTERIOR

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
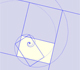
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
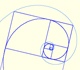
Dos espirales equiangulares contienen los vértices de rectángulos áureos.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.

Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.

Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
|









































































 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR










