Un icosaedro es un sólido platónico. Sus caras son triángulos equiláteros, al igual que el tetraedro y el octaedro.
Ya hemos visto varias propiedades del icosaedro y muchas maneras de construirlo. Tiene una belleza especial y, por otro lado, es muy sencillo de construir.
Por ejemplo, esta lámpara icosaédrica hecha con cartulina y gomas elásticas:

El icosaedro está relacionado con el pentágono y la proporción áurea.


Además hemos visto una construcción muy bonita que muestra que los 12 vértices del icosaedro están en tres rectángulos áureos perpendiculares dos a dos.

En esta página vamos a calcular el volumen del icosaedro.
Parece una tarea complicada pero no lo es si sabemos mirar en su interior y aplicamos dos herramientas básicas:
1) El cálculo del volumen de una pirámide pues podemos imaginarnos el icosaedro formado por pirámides cuya base es una cara que es un triángulo equilátero.
2) Necesitamos saber la altura de esas pirámides, es decir la distancia de una cara al centro del poliedro. Es ahora cuando necesitamos mirar el interior del poliedro para poder calcular esta altura pero veremos que es una sencilla aplicación de la semejanza de triángulos.
También tenemos que recordar alguna propiedad del número áureo.
Vamos a ver lo sencillo que esto. Quizás antes venga bien un repaso de algunas ideas sobre la semejanza y sobre el cálculo del área de un triángulo equilátero.
Usaremos la siguiente notación:
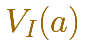
que podemos leer: "Volumen del icosaedro de arista a".
Para saber calcular el área de un icosaedro cualquiera podemos tener en cuenta que nos basta con saber el área de un icosaedro particular, el que nosotros queramos, pues hay una importante relación entre el volumen de figuras semejantes. Aplicado al caso del icosaedro, esta relación se podría expresar diciendo que la razón entre el volumen de dos icosaedros es igual al cubo de las razones de sus aristas.
Si pensamos que una de las aristas mide 1 podemos considerar esta relación:
Ya hemos visto cuando calculábamos el área de un triángulo equilátero que el triángulo equilátero con el que se hacen las operaciones con mucha sencillez es el que tiene lado 2.
Queremos calcular el volumen del icosaedro de arista 1 pero como es más sencillo hacer los cálculos con el de lado 2 vamos a fijarnos en el icosaedro de arista 2.
De todos modos, la relación entre los volúmenes de los icosaedros de arista 1 y 2 es:
Es decir, el volumen de un icosaedro de arista 2 es ocho veces el volumen de un icosaedro de arista 1.
Que también podemos escribir:
Podemos conseguir un octavo de icosaedro justamente seccionándolo por tres planos perpendiculares como los que contienen los tres rectángulos áureos.
Además, al seccionar el icosaedro podremos ver su interior, que es lo que nos interesa.
La aplicación interactiva nos muestra cómo se divide el icosaedro en ocho partes.


Esta división del icosaedro en ocho partes nos va a ser útil, pero para calcular el volumen de un icosaedro podemos imaginarnos que el sólido está formado por 20 pirámides que tienen por base cada una de las caras y cuyo vértice está en el centro del icosaedro.
Usaremos la siguiente notación
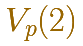
para referirnos al volumen de cada una de las pirámides del icosaedro de arista 2.
Entonces podemos afirmar:
O también:
Tenemos que calcular el volumen de estas pirámides.
El área de la base es sencilla pues es un triángulo equilátero de lado 2, por tanto es:
La pequeña dificultad está en calcular la altura de esta pirámide, es decir la longitud del segmento que va del centro del icosaedro perpendicular hasta la base. Para calcularla haremos uso de la semejanza de triángulos y de nuestra capacidad para ver el interior del icosaedro.
Para ello nos vamos a ayudar de una de esas ocho piezas en las que hemos dividido nuestro poliedro.
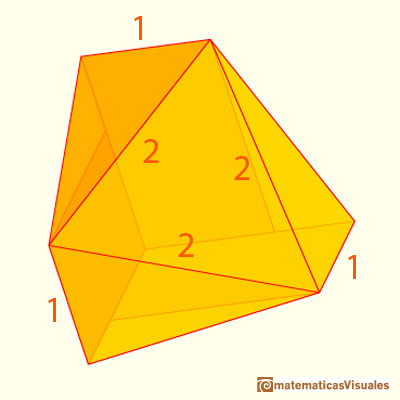
Manipular un modelo en cartulina todavía nos ayuda más a comprender el icosaedro (más abajo hay una plantilla para descargar y montar esta figura):

De paso nos fijamos en que calcular el volumen de un icosaedro de arista 1 es lo mismo que calcular el volumen de esta pieza que es un octavo del icosaedro de arista 2.
Así vemos el interior del icosaedro:
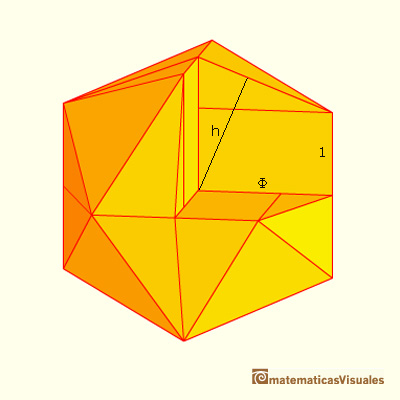

En esta posición tenemos que localizar dos triángulos rectángulos semejantes (¿por qué son semejantes?) y fijarnos en sus hipotenusas y su cateto "largo". El segmento h es la altura de la pirámide pues va perpendicular desde el centro del poliedro a una de las bases (de hecho va a parar al baricentro del triángulo equilátero y, además, es el inradio o radio de la esfera inscrita en el icosaedro).
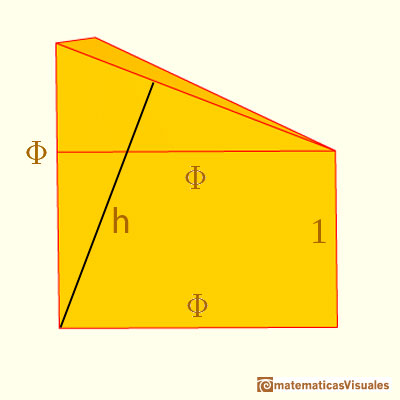
Podemos escribir la proporción:
Despejando h:
Para simplificar los cálculos nos conviene recordar esta propiedad del número áureo.
Entonces h (altura de la pirámide o inradio) puede simplificarse así:
El volumen de una pirámide es:
Y en volumen de un icosaedro de lado 1 es:
El vídeo del comienzo de la página nos ha ayudado a comprender cómo dividir el icosaedro en octavos pero, si te gusta construir poliedros siempre es mucho mejor manipular un objeto real.
He preparado unas plantillas para descargar un octavo de icosaedro. Se necesitan dos versiones simétricas si queremos completar la figura.
Podemos usar estas piezas para completar la construcción de los tres rectángulos áureos y es un ejemplo del uso de imanes para hacer descomposiciones de poliedros.
Aquí vemos cómo usar imanes:

Podemos combinar esta construcción con los tres rectángulos áureos:





Variantes de la construcción de un octavo de icosaedro:

Hemos visto una manera de calcular el volumen de un icosaedro. Hay otro modo que es bastante sencillo y que se basa en una construcción preciosa del icosaedro dentro del octaedro.

En la siguiente página se justifica cómo se puede hacer esta construcción usando diferentes técnicas, se repasa alguna propiedad del octaedro y del icosaedro y se usa para calcular el volumen del icosaedro. Belleza y resultados matemáticos.

REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES