Podemos ver el teorema de Pitágoras en un mosaico. Es una demostración gráfica sencilla del teorema de Pitágoras que vemos en suelos cuando se combinan cuadrados de dos tamaños.

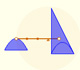Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro aumentado.

En esta segunda versión del rombicuboctaedro aumentado podemos separar las pirámides y ver el interior de la figura. Luca Pacioli escribió que 'podemos ver el interior solo con nuestra imaginación'. La aplicación interactiva solo nos ayuda a ello.

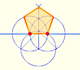En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

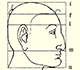Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes.

Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.

Traducción del artículo 'Kepler: The Volume of a Wine Barrel' publicado en 2012 en Convergence ('Convergence: Where Mathematics, History, and Teaching Interact'), revista digital de la Mathematical Association of America.

Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes. En esta página repasamos un problema de optimización.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

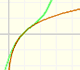Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.