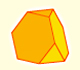
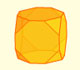
Rombicuboctaedro (adaptado de Leonardo da Vinci)
Este vídeo se basa en una aplicación interactiva. Es una adaptación del dibujo que Leonardo da Vinci hizo del rombicuboctaedro (Vigintisex basium planus vacuus) para el libro 'La divina proporción' de Luca Pacioli.
Pacioli describe así este poliedro:
"Otro cuerpo muy distinto de los ya nombrados, Excelso Duque, es el llamado cuerpo de veintiséis bases, de hermosísimo principio y
origen derivado. De sus veintiséis bases, dieciocho son cuadradas, equiláteras y rectángulas, y ocho triangulares, igualmente
equiláteras y equiángulas. Tiene cuarenta y ocho lados o líneas y noventa y seis ángulos superficiales, setenta y dos de los
cuales son rectos -los de sus dieciocho bases cuadradas- y veinticuatro agudos -los de sus ocho triángulos equiláteros-.
Estos noventa y seis ángulos superficiales determinan la formación de dicho cuerpo de veinticuatro ángulos sólidos, cada uno
de los cuales consta de un ángulo superficial del triángulo y tres ángulos rectos de tres cuadrados. Y de sus cuarenta y ocho
líneas, veinticuatro son comunes a los triángulos y a los cuadrados, ya que de sus dieciocho cuadrados, debidamente unidos entre
sí, resultan necesariamente los ocho triángulos, como se ha dicho a proposito de los otros abcisos. El origen de este cuerpo
es el hexaedro uniformemente cortado en todas sus partes, como nos muestra a la vista su propia forma material. Su conocimiento
resulta utilísimo por muchas consideraciones para quien bien lo sepa aplicar, sobre todo en arquitectura. Y esto por lo que
respecta al conocimiento de su sólido plano o hueco."
('La divina proporción' de Luca Pacioli, página 97, traducción de Juan Calatrava, Editorial Akal, 4ª edición, 2008)
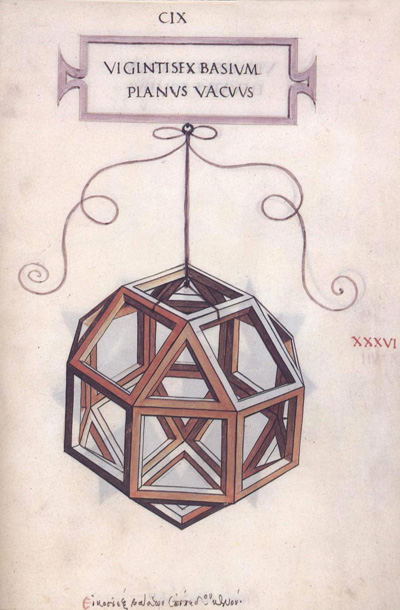
Dibujo de Leonardo da Vinci del rombicuboctaedro (Vigintisex basium planus vacuus) para el libro 'La divina proporción' de Luca Pacioli. (Hay versión española del libro 'La divina proporción' en Editorial Akal. La imagen se usa con permiso de la Editorial Akal).

Dibujo de Leonardo da Vinci del rombicuboctaedro (Vigintisex basium planus solidus) para el
libro 'La divina proporción' de Luca Pacioli. (Hay versión española del libro 'La divina proporción' en Editorial Akal. La imagen se usa con permiso de la Editorial Akal).
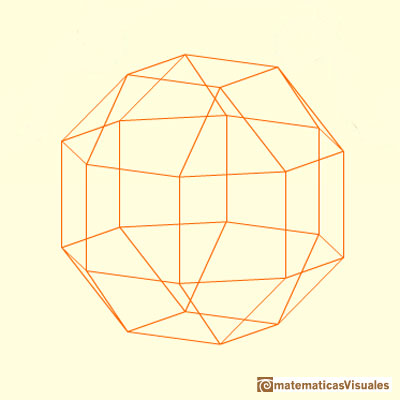
En la aplicación interactiva podemos rotar el poliedro y jugar con el "agujero" en cada cara:




Es sencillo y recomendable construir un rombicuboctaedro con cartulina:

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.



Con Microarquitectura podemos construir un rombicuboctaedro.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

Una lámpara en Edam (Holanda):

Edam (Holanda), 2016

Ramblas de Barcelona, 2018

Variación sobre el rombicuboctaedro en Sauveterre-de-Béarn (Francia), 2018
Este dado de marfil se basa en el rombicuboctaedro. Se llama dado de Carlos V y se puede ver en el Museo Lázaro Galdiano (Madrid, España). Ángel Requena escribió una referencia a este objeto en su sitio web Turismo Matemático. También escribió un artículo sobre este dado poliédrico.

Museo Lázaro Galdiano (Madrid, España), 2018
Reloj de sol en el Deutsches Museum (Museo de Ciencia) en Munich. Tiene la forma de un rombicuboctaedro.

Reloj de sol en el Deutsches Museum (Museo de Ciencia, Munich, Alemania), 2016

Reloj de sol en el Deutsches Museum (Museo de Ciencia, Munich, Alemania), 2016

Reloj de sol en el Deutsches Museum (Museo de Ciencia, Munich, Alemania), 2016
REFERENCIAS
Luca Pacioli - La divina proporción - Ediciones Akal, 4ª edición, 2004. Traducción de Juan Calatrava.
Leonardo da Vinci's Geometric Sketches artículo de Frank J. Swetz en MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra página de George Hart en su excelente sitio sobre poliedros.
Turismo Matemático, sitio web
de Ángel Requena con muchas fotografías de objetos matemáticos y muy interesantes comentarios. Varias de sus entradas están dedicadas al rombicuboctaedro.
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES

En esta segunda versión del rombicuboctaedro aumentado podemos separar las pirámides y ver el interior de la figura. Luca Pacioli escribió que 'podemos ver el interior solo con nuestra imaginación'. La aplicación interactiva solo nos ayuda a ello.

También llamado girobicúpula cuadrada elongada. Es muy parecido al rombicuboctaedro pero es menos simétrico.

A partir de un rombicuboctaedro podemos añadir pirámides a sus caras. Obtenemos un precioso poliedro que parece una estrella.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.