|
|
Poliedros duales: el cubo y el octaedro
Taller de Talento Matemático (Zaragoza)
Sesión del Taller de Talento Matemático de Zaragoza por Roberto Cardil.
Viernes día 18 de noviembre de 2022, a las 18:15 en la Facultad de Matemáticas de la Universidad de Zaragoza.
Este es un cartel de la sesión. Se puede descargar e imprimir:
Esta sesión del Taller de Talento Matemático es
parecida a la que se realizó en octubre de 2015.
Objetivos:
Como en ocasiones anteriores, el principal objetivo es pasar un buen rato hablando de algunos poliedros.
En esta sesión nos vamos a fijar en idea de dualidad, es decir, que de algún modo, los poliedros están emparejados.
Podemos empezar por los poliedros más regulares (los llamados sólidos platónicos) y, en particular por la pareja más
sencilla, la que forman el cubo y el octaedro.
También queremos animar a la construcción de poliedros con diferentes técnicas sencillas (papiroflexia, cartulina, tubos, gomas, Zome, etc.).
Queremos construir poliedros para disfrutar de su belleza, mejorar nuestra percepción espacial y obtener conclusiones matemáticas.
Tendremos que hacer una construcción, para cogerle gusto. En esta sesión haremos un octaedro con papiroflexia que
podemos encerrar en una caja que es un cubo.
Necesitaremos tijera, regla y pegamento.
También papel y lápiz, para hacer alguna cuenta.
Aquellos que ya habéis construido algún poliedro en vuestra casa lo podéis traer para animar a todos a construir.
Los poliedros nos ayudan a pensar.
Esta sesión tiene un espíritu parecido a otras del Taller de Talento Matemático en las que se ha realizado
alguna construcción de poliedros. Por ejemplo, las siguientes:

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
Puedes ver más enlaces a otras construcciones de poliedros al final de esta página.

1.- Los cinco sólidos platónicos
Los cinco sólidos platónicos son los poliedros más regulares. Todas sus caras son congruentes (iguales) y son un polígono regular.
Resulta que estos polígonos regulares que forman las caras de cada sólido platónico sólo pueden ser triángulos equiláteros, cuadrados y pentágonos.
En los vértices de cada poliedro concurren el mismo número de aristas.
Estos son los cinco sólidos platónicos o poliedros regulares construidos con diferentes técnicas.
Tetraedro:
Cubo:
Octaedro:
Icosaedro:
Dodecaedro:
INVESTIGA
¿Por qué la unión de dos tetraedros no es un sólido platónico?

2.- Dualidad entre poliedros
El interés por los poliedros se remonta a tiempos muy remotos.
Se produce un cambio fundamental en la visión que tenemos de los poliedros con los trabajos de Leonard Euler (1707-1783).
Euler se fijó en propiedades de los poliedros que no tienen que ver con las medidas (de los lados, de los ángulos, etc.).
Consideró que los elementos fundamentales de un poliedro eran sus caras (de dimensión 2), sus aristas (de dimensión 1)
y sus vértices (puntos, de dimensión 0).
Vamos a contar estos elementos de los sólidos platónicos:
Podemos formar parejas de poliedros que llamamos duales si nos fijamos que hay
parejas de poliedros que intercambian el número de caras y vértices y tienen el mismo número de aristas.
A pesar de que estos conceptos se aplican a muchos poliedros y son propiedades que no están relacionadas con la medida de superficies, ángulos o aristas
vamos a ver la dualidad de varios de estos sólidos platónicos.
INVESTIGA
Fórmula de Euler para los poliedros.
Además para estos poliedros (y para los poliedros irregulares que no tienen agujeros, que si nos imaginamos que se pueden
inflar, al hincharlos quedarían como una pelota) se verifica una importante fórmula (que debemos a Leonard Euler) que
relaciona las caras, las aristas y los vértices de un poliedro.

3.- El dual de un tetraedro es otro tetraedro
Un tetraedro tiene cuatro caras y cuatro vértices. Por lo tanto, su poliedro dual (intercambiando caras con vértices)
tiene 4 caras y 4 vértices, es decir, es otro tetraedro
En una pareja de poliedros duales, cada cara se corresponde con un vértice del otro (y viceversa).
En el caso de los sólidos platónicos podemos construir un poliedro dentro de su poliedro dual considerando que los
vértices de uno de ellos están en los centros de las caras del otro.
Entonces una construcción de un tetraedro y su dual es la siguiente:
Esta construcción ya nos la mostró Kepler (1571-1630):
INVESTIGA

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

4.- Dos tetraedros en posición recíproca: Stella Octangula
Ahora nos vamos a fijar en que cada pareja de poliedros duales tiene el mismo número de aristas.
Para el caso de los poliedros platónicos duales una posible construcción es colocar la pareja de poliedros duales
de modo de cada arista esté bisecada por la otra y, además, en ángulo recto.
Entonces decimos que están en 'posición recíproca'.
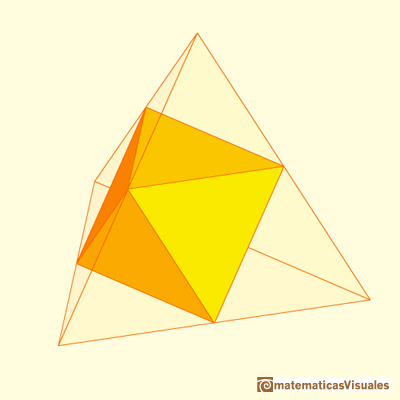
En el caso del tetraedro obtenemos un poliedro que Kepler llamó 'Stella Octangula'.
Si nos fijamos en la figura que es común a los dos tetraedros vemos que es un octaedro.
La Stella Octangula la podemos ver como un octaedro al que se le han añadido unas pirámides en cada cara. De hecho estas
pirámides son también tetraedros.
La Stella Octangula es un ejemplo de poliedro que llamamos estrellado, recibe también el nombre de 'octaedro estrellado'.
Si unimos adecuadamente los vértices de la Stella Octangula obtenemos un cubo.
Hemos obtenido, por un lado, un octaedro (interior) y, por otro, un cubo (exterior). Vamos a ver que el cubo y el octaedro forman también
una pareja de poliedros duales.
INVESTIGA

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

5.- El tetraedro truncado
Nos fijamos ahora en un solo tetraedro. Contiene un octaedro.
Podemos pensar que obtenemos un octaedro a partir de un tetraedro cortando unas 'esquinas' (en este caso lo que
cortamos son tetraedros).
Este procedimiento se llama truncamiento.
Según la profundidad del truncamiento obtenemos diferentes poliedros. En algunos casos obtenemos poliedros de una familia que
llamamos poliedros arquimedianos.
Por ejemplo, el tetraedro truncado.
INVESTIGA
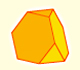
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.

6.- El cubo y el octaedro son poliedros duales
Si contamos las caras, aristas y vértices del cubo obtenemos:
Si contamos las caras, aristas y vértices del octaedro obtenemos:
Se intercambian las caras y los vértices y ambos poliedros tienen el mismo número de aristas.
El cubo y el octaedro son poliedros duales.
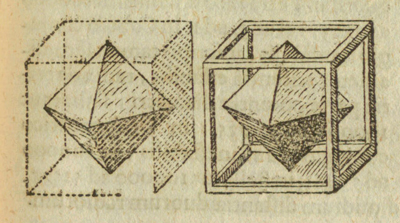
Podemos colocar un octaedro dentro de un cubo con cada vértice del octaedro en el centro de una cara del cubo.
Así nos lo mostró Kepler:

7.- El cubo y el octaedro en posición recíproca
Si colocamos un cubo y un octaedro en 'posición recíproca' obtenemos este poliedro:
El poliedro común se llama cuboctaedro.
El poliedro que se forma al colocar un cubo y un octaedro en 'posición recíproca' es un cuboctaedro estrellado.
Podemos ver el cuboctaedro como un truncamiento.
Si unimos los vértices del cuboctaedro estrellado obtenemos un poliedro que se llama dodecaedro rómbico.
El dodecaedro rómbico y el cuboctaedro son poliedros duales.
INVESTIGA

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

8.- El cuboctaedro
El cuboctaedro, al igual que el tetraedro truncado, es un poliedro arquimediano.
Sus caras son cuadrados y triángulos equiláteros.
INVESTIGA

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

9.- El dodecaedro rómbico
El dodecaedro rómbico iene 12 caras que son rombos.
Tesela el espacio, es decir, con dodecaedros rómbicos podemos llenar el espacio sin dejar huecos.
Está relacionado con la construcción de los panales de las abejas.

10.- El cubo truncado
Hemos visto que el cuboctaedro es el sólido común a un cubo y un octaedro en 'posición recíproca'.
Podemos ver el cuboctaedro como un truncamiento de un cubo.
Si truncamos un cubo con 'menor profundidad' obtenemos otro poliedro arquimediano que llamamos cubo truncado.
Sus caras son octógonos y triángulos equiláteros.
INVESTIGA
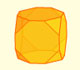
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

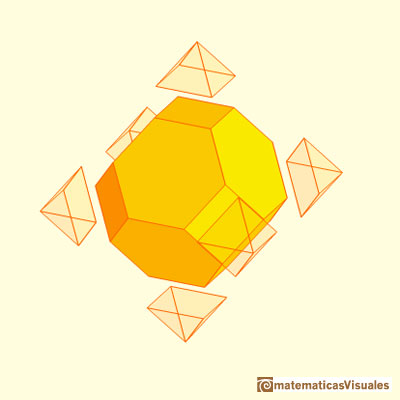
11.- El octaedro truncado
También podemos ver el cuboctaedro como un truncamiento de un octaedro.
Si truncamos el octaedro con 'menor profundidad' podemos obtener otro sólido arquimediano que llamamos
octaedro truncado. Sus caras son hexágonos y cuadrados.
Al igual que el dodecaedro rómbico, el octaedro truncado tesela el espacio.
INVESTIGA

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

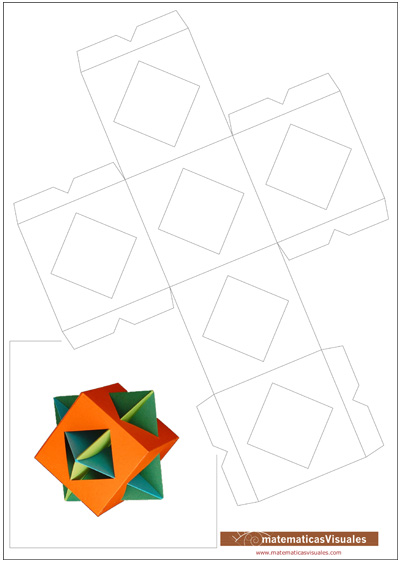
12.- Construcción de un octaedro dentro de un cubo
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales
dos a dos que contienen las 12 aristas y los 6 vértices del
octaedro regular.
Su construcción es simple y aquí podemos ver cómo se hace:
El objetivo es, además, construir una cubo para poder poner dentro el octaedro que hemos hecho con papiroflexia.
El cuadrado de la izquierda representa el tamaño del cuadrado de papel que tenemos que usar para construir el octaedro.
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE SIGUIENTE

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
 ANTERIOR ANTERIOR

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.

Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.

Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
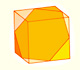
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
|









































































 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR























