|
|
Volúmenes de pirámides, del tetraedro y del octaedro
Taller de Talento Matemático (Zaragoza)
En esta sesión tenemos dos objetivos:
OBJETIVO 1
Queremos pasar un rato hablando de poliedros. En esta ocasión vamos a estudiar algunas pirámides. Repasaremos la fórmula para calcular el
volumen de una pirámide y veremos que no es tan simple como pudiera parecer. En algunos casos, las pirámides son sencillas y para calcular su volumen no hace falta
la fórmula. ¿Seremos capaces de calcular el volumen del tetraedro y el del octaedro sin usar esa fórmula?
OBJETIVO 2
El objetivo principal es construir alguna figura geométrica y
animar a la construcción de poliedros con diferentes técnicas sencillas (papiroflexia, cartulina, tubos, gomas, Zome, etc.).
Queremos construir poliedros para disfrutar de su belleza, mejorar nuestra percepción espacial y obtener conclusiones matemáticas.
Veremos que gracias a la construcción que proponemos en esta página podremos obtener el volumen del tetraedro y del octaedro con
bastante facilidad.
Construir y manipular poliedros nos permiten comprenderlos mejor.
La mayor parte del tiempo la dedicaremos a hacer una construcción.
Necesitaremos tijera, regla y pegamento.
También papel y lápiz.
Traed algún poliedro que tengáis por casa. Así todos nos animamos a construir figuras geométricas.
Esta sesión tiene un espíritu parecido a las otras sesiones que hemos realizado sobre poliedros
para el Taller de Talento Matemático de Zaragoza:

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
Ésta es la construcción que vamos a hacer, un tetraedro de origami dentro de un cubo de cartulina:

1.- Polígonos semejantes. Cuadrados y triángulos equiláteros
Vamos a empezar repasando las áreas de cuadrados y triángulos equiláteros pues luego las vamos a necesitar.
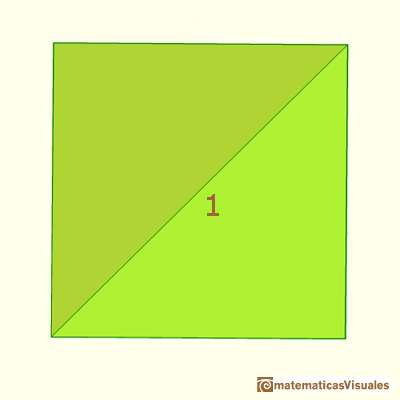
En el caso de estos polígonos regulares nos solemos fijar en el lado. Éste es un cuadrado de lado 1.
El área de un cuadrado de lado 1 la podemos escribir:
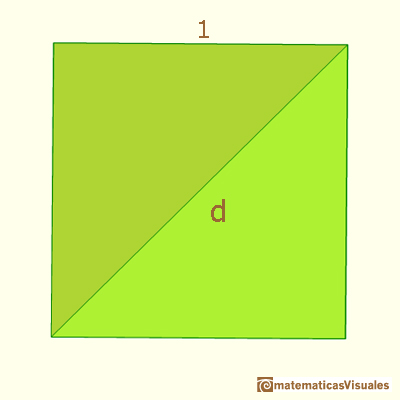
La longitud de la diagonal de un cuadrado de lado 1 se calcula aplicando el teorema de Pitágoras y podemos escribir:
En ambas expresiones hemos puesto el lado (que es 1) entre paréntesis.
El siguiente cuadrado tiene diagonal 1, ¿cuál es su lado?
El lado es lo que nos falta entre paréntesis. Entonces leeremos "la diagonal del cuadrado de lado ..... es igual a 1.
Así podemos escribir el área de un cuadado de lado .... es igual a ....:
Este cuadrado es más grande. Su diagonal es 2. Si la diagonal en este caso es el doble que en el caso anterior, entonces el lado también
será el doble.
El área de este cuadrado la escribimos:
Y su valor es fácil de calcular
Si comparamos estas fórmulas
vemos que si multiplicamos por dos el lado del cuadrado la diagonal también sería el doble pero el área es cuatro veces.
En general se verifica esta fórmula para las áreas de los cuadrados
No es necesario que sean cuadrados. Para dos polígonos semejantes el área cumple esta importante propiedad.
Aplicaremos esta propiedad también en el caso de los triángulos equiláteros.
Si ampliamos o reducimos un polígono (obtenemos un polígono semejante) entonces sus dimensiones 'lineales' se reducen en la misma
proporción. Ya hemos usado esto para la diagonal de un cuadrado.
Una de las cosas que nos dicen estas fórmulas es que para calcular el área de un cuadrado conociendo la diagonal no tengo que aplicar
el teorema de Pitágoras cada vez. Basta con haberlo hecho una vez (que ya lo hemos hecho) y aplicar esta propiedad. Esta propiedad la
hemos aplicado para los cuadrados pero es válida también para triángulos equiláteros y, en general, se cumple para figuras que
tienen 'la misma forma'. Decimos entonces que las figuras son 'semejantes'. (Todos los cuadrados tienen la misma forma, son semejantes.
Todos los triángulos equiláteros tienen la misma forma, son semejantes).
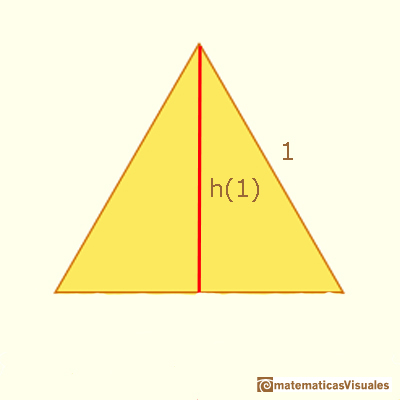
Por ejemplo, para calcular la altura y el área de un triángulo equilátero podemos elegir el caso que más nos convenga, el más sencillo.
Para calcular la altura (que depende del tamaño del lado) de un triángulo equilátero usaremos el teorema de Pitágoras.
¿Cuál es un buen triángulo para hacer esto cálculos?¿Cuál es preferible, el de lado 1 o el de lado 2?
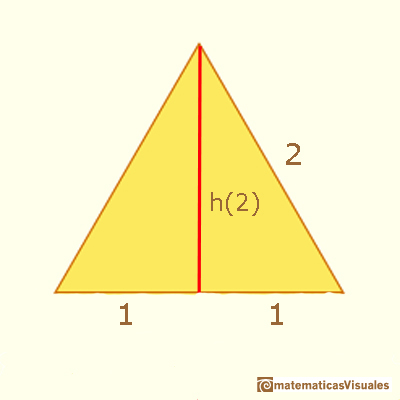
La altura de un triángulo equilátero de lado 2 es ...
Entonces, la altura de un triángulo de lado 1 es:
El área de un triángulo equilátero de lado 2 es muy sencilla:
Se verifica la relación con el de lado 1:
Por lo tanto, el área de un triángulo de lado 1 es:
Se verifica la fórmula general del área de figuras semejantes:
Hemos visto que las longitudes y las áreas de polígonos semejantes tienen las propiedades:

2.- Figuras planas curvilíneas. Circunferencia y círculo
El cálculo de áreas de polígonos no plantea dificultades serias. Solemos usar alguna propiedad geométrica (una que usamos
muy a menudo es el teorema de Pitágoras) y también descomponemos la figura en figuras más sencillas (como si fuera un puzle) que
sabemos calcular y después sumamos todas ellas.
Tampoco plantea dificultad comprobar las propiedades de las longitudes y áreas correspondientes de polígonos semejantes de las
que hemos hablado.
Sin embargo otro asunto es cuando consideramos figuras planas curvilíneas. Los matemáticos de tiempos muy remotos ya eran conscientes
de esto. Se necesitan procedimientos más complicados para hacer estos cálculos y justificar las propiedades. Estos procedimientos
incluyen algún 'proceso infinito', o 'de paso al límite'. Actualmente el estudio de este tipo de procedimientos forma parte del Cálculo
Integral y no están dentro que lo que podemos considerar 'Matemáticas Elementales'.
El caso más simple, el del círculo, ya plantea este tipo de dificultades. Para abordarlas los matemáticos griegos usaron razonamientos
que hacían rigurosos estos cálculos. Uno de ellos es el 'método de exhaución' de Eudoxo que fue usado por Arquímedes. Estamos
hablando de más de 300 años antes de nuestra era (Arquímedes murió en el 212 a.C.).
En Europa tendrían que pasar unos 1800 años para que, en torno a 1600, otros matemáticos hicieran progresos significativos. Las bases
no eran muy sólidas pero los procedimientos fueron efectivos y, muchas veces, intuitivos.
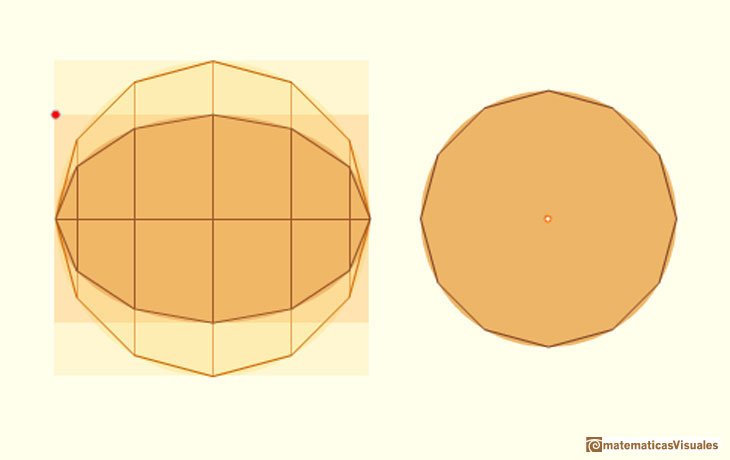
Por ejemplo, Kepler se plantea el área del círculo como un 'proceso infinito' que puedes ver en estas ilustraciones.
Tambien Arquímedes usó argumentos semejantes, por ejemplo, para deducir el área de una elipse:
INVESTIGA
En la siguiente página puedes interactuar con una aplicación que muestra el proceso que usó Kepler para justicar la fórmula
del área del círculo:

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.
Aquí se trata de la elipse:

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

3.- Tres sólidos platónicos: cubo, tetraedro y octaedro
Vamos a repasar los tres poliedros platónicos o regulares que nos interesan para esta sesión.
El Tetraedro es el sólido platónico más sencillo. Conocido desde épocas muy remotas. Sus cuatro caras son triángulos equiláteros.
El cubo tiene seis caras que son cuadrados:
El octaedro tiene ocho caras que son triángulos equiláteros:
El octaedro se puede ver como la unión de dos pirámides de base cuadrada.
Vamos a ver que estos tres poliedros están muy relacionados. Estas relaciones nos van a permitir calcular algunos volúmenes.
INVESTIGA
La relación principal se llama dualidad. Puedes consultar algo más sobre los cinco poliedros
platónicos y sobre la dualidad de los poliedros en los apartados 1 y 2 de este enlace:

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

4.- Volumen del cubo
Ya hemos hablado otras veces sobre el volumen del cubo. Para repasar algunas ideas puede mirar el apartado 3 de:

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
El volumen del cubo de diagonal 1 lo podemos escribir (en función de su arista)
El volumen de un cubo de lado ....
El volumen de este cubo de lado .... es ....
Veamos lo que ocurre con un cubo que tiene una diagonal de la cara igual a 2, es decir, del doble de larga que la del anterior cubo.
La arista de este cubo es por lo tanto el doble de larga también.
Pero el volumen del cubo que tiene el doble del lado es ocho veces más grande:
Para el volumen de cubos se cumple
Esta propiedad se cumple para los cubos y también se puede ver con facilidad para ortoedros semejantes.
De hecho esta relación se cumple para el volumen de figuras semejantes. Sin embargo, la demostración de este hecho no es tan sencilla.

5.- Volumen de las pirámides.
Ya hemos visto que cuando queremos calcular áreas de figuras planas con curvas, por ejemplo, un círculo, necesitamos algún tipo de
'proceso infinito'. Esto hace que sea algo más difícil. Sin embargo no tenemos especial problema en calcular áreas de polígonos,
que tienen todos sus lados rectos.
En el caso de los volúmenes la situación se complica y ya necesitamos ese tipo de 'proceso infinito' para justificar el cálculo
del volumen de una pirámide en general.
En torno a 1600 varios matemáticos retoman este tipo de problemas, podemos decir que continuando los trabajos de Euclides, Arquímedes y
otros matemáticos griegos.
Plantean diferentes tipos de soluciones que son antecedentes del gran logro que es el desarrollo del Cálculo por Newton y Leibniz.
Vamos a citar muy brevemente dos de esos antecedentes que son los trabajos de Kepler y de Cavalieri.
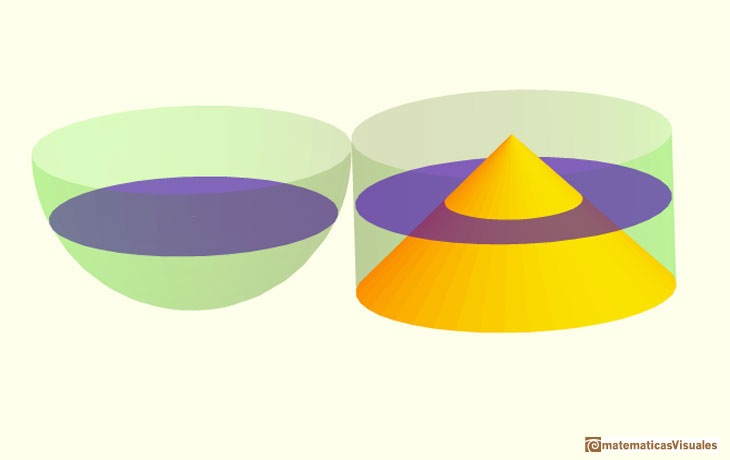
Johanes Kepler se plantea la descomposición de la figura en partes que tienen el volumen tan pequeño como el quiera. Por ejemplo, en rodajas
con un altura muy muy pequeña. La suma de todas ellas aproxima el volumen de la figura en cuestión.
Lo podemos aplicar a otras figuras curvilíneas, por ejemplo, conos y barriles
El planteamiento de Buenaventura Cavalieri es un poco distinto. Cavalieri compara figuras a partir de secciones o cortes de la figura. Si dos
figuras tienen todas sus secciones iguales también tendrán sus volúmenes iguales.
En la siguiente ilustración vemos una aplicación de este método para calcular el volumen de una esfera.
Con estas herramientas, que posteriormente se harían rigurosas, podemos obtener resultados poderosos.
Podemos afirmar que el volumen de dos pirámides que tienen la misma área de la base y la misma altura tienen volúmenes iguales.
También podemos deducir la fórmula del volúmenes de las pirámides en general que es un tercio del área de la base por la altura. Que
también sirve para calcular el volumen de conos.
INVESTIGA
En las siguientes páginas ampliar información sobre los métodos de Cavalieri y Kepler.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes.

6.- Una pirámide que es un tercio de un cubo
Hay algunos ejemplos de pirámides particularmente sencillas. No necesitamos la fórmula para calcular su volumen.
Al contrario, estos ejemplos sencillos nos permiten ver que la fórmula general del volumen de las pirámides se cumple
en estos casos particulares.
Lo podemos hacer por descomposición. Podemos descomponer un cubo en tres pirámides iguales y está claro que se cumple la fórmula.

7.- Una pirámide de base cuadrada que es un sexto de un cubo
Vamos a ver otro ejemplo sencillo de una pirámide que tiene un volumen fácil de calcular.
Si consideramos el centro de un cubo y unimos ese punto con los ocho vértices del cubo obtenemos seis pirámides iguales.
Si lo desplegamos vemos las seis pirámides.
Aquí vemos la construcción en cartulina:
Si el cubo tiene arista 1, su volumen es también 1 y el volumen de cada una de las pirámides es un sexto. Si piensas cuanto mide
la altura de cada pirámide podrás ver que está claro que se verifica la fórmula del volumen de la pirámide en este caso particular.
Lo curioso de esta construcción es que si plegamos las pirámides hacia fuera sobre otro cubo
Se forma un nuevo poliedro muy interesante que tiene doce caras rómbicas y que se llama dodecaedro rómbico. Fue descrito por primera vez por
Kepler.
Este es un modelo hecho con cartulina:
INVESTIGA
Puedes ver muchas más cosas sobre el dodecaedro rómbico y su relación con los panales de las abejas siguiendo el siguiente enlace:

Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.

8.- Una pirámide que es un tercio de un prisma
Veamos ahora un ejemplo interesante pero que ya no es tan simple. No es tan sencillo imaginárselo pero si se ve y se toca enseguida se
comprende. Un buen ejemplo de que manipular objetos geométricos nos ayuda a comprender conceptos matemáticos.
Tenemos un prisma triagular (en nuestro caso la base del prisma es un triángulo equilátero, pero esto es un detalle. Lo que vamos a ver se
verifica para cualquier prisma triangular). El volumen del prisma es área de la base por la altura.
El prisma se puede descomponer en tres pirámides:
De estas tres pirámides, dos son iguales y, claramente, tienen el mismo volumen.
Pero la tercera es distinta. Sin embargo podemos ver que esta tiene la misma base y la misma altura que las otras dos.
Ya hemos visto que una
consecuencia del Principio de Cavalieri era que si dos pirámides tienen la misma área de la base y la misma altura entonces las dos tienen
el mismo volumen.
Por lo tanto, las tres pirámides tienen el mismo volumen que es un tercio del volumen del prisma.
Por lo tanto, también en este caso se verifica la fórmula del volumen de la pirámide que es un tercio del área de la base por la altura.
Hemos de notar que este ejemplo es un poco diferente a los dos anteriores pues las pirámides no son iguales. Hemos que tenido que
utilizar un argumento más, de hecho, hemos utilizado uno muy potente como es el Principio de Cavalieri, es decir, una propiedad
relacionada con esos 'procesos infinitos' de los que hemos hablado antes.

9.- Volumen del octaedro (usando la fórmula)
Podemos pensar que el octaedro está formado por dos pirámides de base cuadrada unidas. Su desarrollo es fácil de
construir pues sus caras son triángulos equiláteros.
Vamos a usar la fórmula del volumen de las pirámides para calcular el volumen del octaedro. Parece que no es sencillo pero si
tenemos un octaedro en la mano resulta mucho más simple.
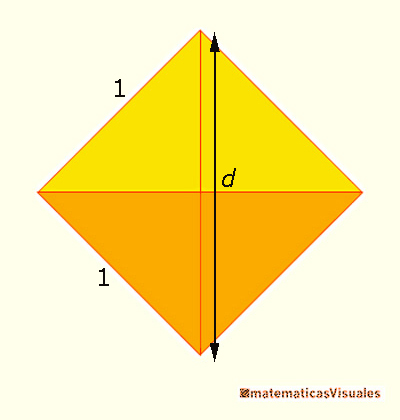
Para calcular el volumen del octaedro vamos a fijarnos en que este poliedro tiene sus 12 aristas formando 3 cuadrados:
La altura de estas dos pirámides es una diagonal de un cuadrado.
Si, por ejemplo, el lado es 1 entonces la base tiene 1 de área y la altura de las
dos pirámides es la diagonal de un cuadrado unitario.
La diagonal de un cuadrado de lado 1 es:
Por lo tanto, el volumen de un octaedro de lado 1 es:
Y el volumen de un octaedro de lado a es:
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales
dos a dos que contienen las 12 aristas y los 6 vértices del
octaedro regular.
INVESTIGA
En el apartado 12 de la siguiente página puedes ver la construcción de este octaedro.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
Usando la fórmula del volumen de la pirámide (que es un tercio del área de la base por la altura) y mirando
adecuadamente un octaedro vemos que es muy sencillo calcular su volumen.
Todavía no sabemos el volumen de un tetraedro. Además queremos calcular estos volúmenes sin recurrir a la fórmula, sólo
utilizando la propiedad de los volúmenes de figuras semejantes.

10.- Volumen de figuras semejantes
Queremos ver una propiedad muy importante que relaciona el volumen de figuras semejantes.
Esta propiedad nos permitirá calcular de un modo muy sencillo el volumen del tetraedro y el del octaedro.
Pero esta propiedad no es sencilla de probar. Al igual que pasa con la fórmula del volumen de las pirámides, en este caso
también necesitamos algún 'proceso infinito'.
Hemos visto que las longitudes y las áreas de polígonos semejantes tienen las propiedades:
Es decir que si tenemos dos figuras semejantes y comprobamos una longitud y vemos que la figura semejante es el doble
entonces todas las longitudes de esta figura semejante serán el doble que sus correspondientes de la primera figura.
Si consideramos dos cuadrados y el segundo tiene el lado que mide el doble que el primero entonces podemos decir que
su diagonal también mide el doble.
Si consideramos dos triángulos semejantes y el segundo tiene la base que es el doble, entonces su altura también es el
doble que la del primero.
Sin embargo, el área de estas figuras será cuatro veces más.
Esta propiedad es sencilla de probar si consideramos polígonos semejantes. Pero ya hemos visto que si consideramos figuras con
curvas ya no es tan simple y necesitamos algún tipo de 'paso al límite'.
En el caso de los volúmenes de cubos también hemos visto que se cumple una propiedad análoga
Es decir que si un cubo tiene una arista que es el doble que otro el volumen del grande es ocho veces el del pequeño.
Esta propiedad se verifica también para ortoedros en general pero en cuanto consideramos otros poliedros, como puedan ser
las pirámides, ya nos encontramos con la necesidad de recurrir a 'procesos infinitos'. La demostración no es tan elemental.
Sin embargo esta fórmula se cumple y nosotros vamos a aceptarla y a aplicarla en el caso del tetraedro.
Si consideramos dos tetraedros, el grande tiene la arista doble que la del pequeño entonces el volumen del tetraedro
grande es ocho veces el del pequeño.
En general es cierto que se verifica la siguiente relación para el volumen de figuras semejantes:

11.- Relación entre el volumen del tetraedro y el del octaedro
Una manera de construir nuevos poliedros es añadir pirámides a las caras de otro poliedro.
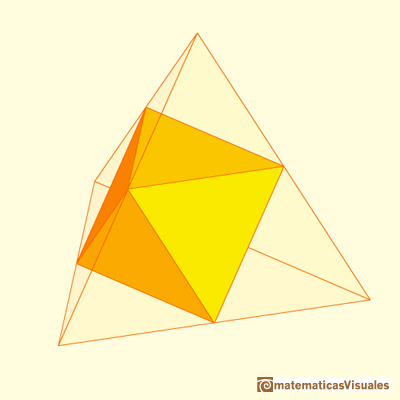
Un ejemplo interesante es partir de un octaedro de arista 1 (por ejemplo) y añadirle cuatro tetraedros:
Lo que obtenemos un tetraedro más grande, que tiene de arista 2:
Podemos escribir la relación (volumen de figuras semejantes):
Por otro lado, vemos que este tetraedro de arista 2 está formado por un octaedro y cuatro tetraedros de arista 1:
Entonces, el volumen
del octaedro es cuatro veces el del tetraedro
Ahora ya podríamos saber el volumen del tetraedro puesto que hemos podido calcular
el del octaedro con ayuda de la fórmula del volumen de una pirámide.
Queremos ver si podemos calcular estos volúmenes sin usar la fórmula, sólo con la propiedad que relaciona los volúmenes de
tetraedros semejantes.

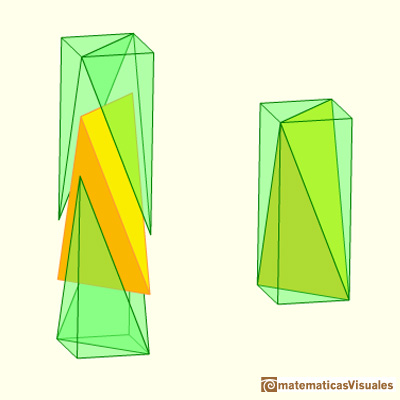
12.- Un tetraedro dentro de un cubo. Volumen del tetraedro
Lo que queremos es un procedimiento sencillo para calcular el volumen del tetraedro (y el del octaedro) sin usar la fórmula
del volumen de la pirámide.
Vamos a ver una construcción (que ya nos enseñó Kepler) que nos va a facilitar la tarea.
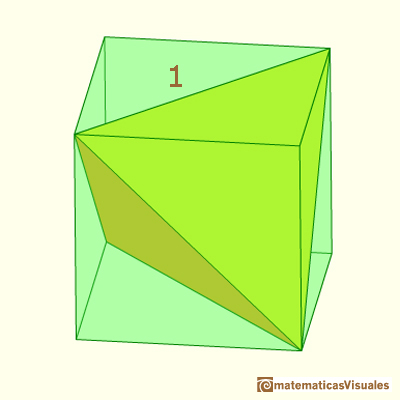
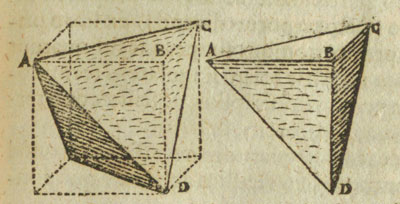
Se puede construir un tetraedro dentro de un cubo:
Tomando dos diagonales de dos caras opuestas de un cubo y uniéndolas adecuadamente obtenemos un tetraedro.
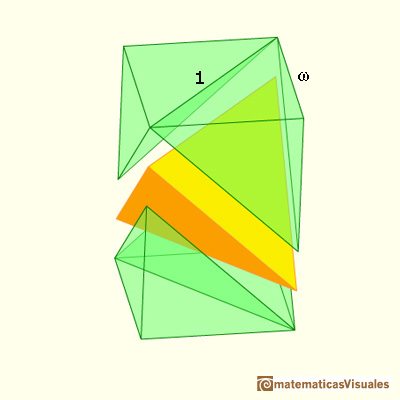
Ponemos el tetraedro dentro del cubo y quedan unos huecos que podemos rellenar con las piezas verdes.
Vamos a ver que el volumen de un tetraedro es un tercio del volumen del cubo que lo contiene.
Si la arista del tetraedro es 1 entonces la arista w del cubo es:
El volumen de este cubo lo hemos escrito así:
El cubo está compuesto por el tetraedro amarillo y dos pares de pirámides verdes.
Pero estas cuatro piezas verdes forman medio octaedro.
Y sabemos que medio octaedro tiene el mismo volumen que dos tetraedros.
Dos tercios del volumen del cubo está ocupado por las pirámides verdes. Entonces al tetraedro amarillo le queda el tercio restante.
Por lo tanto, el volumen del tetraedro del arista 1 es:
Entonces, el volumen del tetraedro regular de arista a es:
A partir de esto y de las propiedades de la semejanza (pero sin usar la fórmula del volumen de la pirámide) ya podemos volver a
calcular el volumen del octaedro (que es cuatro veces el del tetraedro con la misma arista):
Esta construcción puede generalizarse para cualquier paralelepípedo y obtenemos "tetraedros" no regulares.
El volumen de estos tetraedros es también un tercio del volumen del paralelepípedo que los contiene.

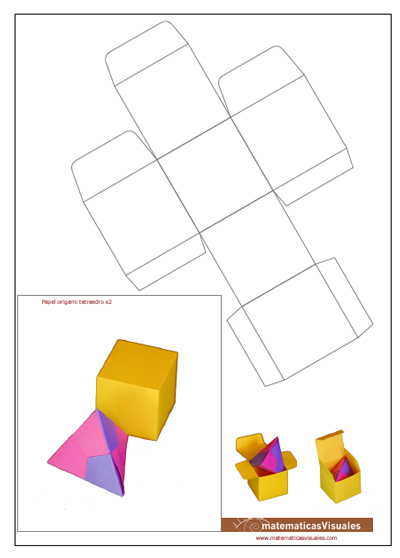
14.- Construcción de un tetraedro con origami
Para terminar vamos a construir dos figuras usando dos técnicas básicas: origami y cartulina pegada.
Con origami construiremos un tetraedro que podremos poner dentro de una cajita cúbica hecha con cartulina.
Este es el modelo de la caja cúbica que se pueden descargar. El rectángulo es el tamaño de papel que necesitamos para el plegado de un
tetraedro que cabe perfectamente en la caja:
Estas son las instrucciones para el plegado del tetraedro con origami modular:
Me gustaría haber podido transmitir gusto por la construcción de poliedros y la idea de que además de la belleza que tienen tambien su manipulación
nos permite hacer razonamientos matemáticos de un modo sencillo. Ver y tocar las Matemáticas.
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE SIGUIENTE

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.
 ANTERIOR ANTERIOR

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
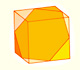
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
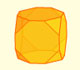
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.
|


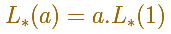
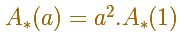



































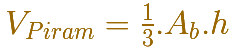























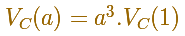
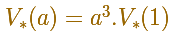



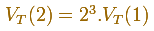


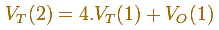










 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR



















