Bonaventura Cavalieri(1598-1647) fue un matemático italiano. Fue un precursor del cálculo infinitesimal. Cavalieri, Kepler y otros matemáticos que vivieron durante el siglo que precede a Newton y Leibniz, inventaron y usaron métodos infinitesimales intuitivos para resolver problemas de áreas y volúmenes.
Veinte años después de la publicación del libro de Kepler, Stereometria Doliorum, Cavalieri escribió un libro muy popular: Geometria indivisibilibus (1635).
En este libro, el matemáticos italiano usó lo que ahora conocemos como Principio de Cavalieri: Si dos sólidos tienen las alturas iguales y si las secciones hechas por planos paralelos a las bases a la misma distancia de la base están en una determinada proporción, entonces los volúmenes de los sólidos están también en esa proporción.
El Principio de Cavalieri se conoce también como el método de los indivisibles. "Cavalieri hizo de la noción de indivisible la base de un método geométrico de demostración. No explicó precisamente lo que entendía por la palabra indivisible que empleó para caracterizar los elementos infinitesimales que usó en su método. Cavalieri concibió una superficie como formada por un número indefinido de líneas paralelas equidistantes y un sólido como compuesto por planos paralelos equidistantes, y designa estos elementos los indivisibles de la superficie y del volumen respectivamente." (C.H. Edwards)
Zu Geng, que nació hacia el año 450, fue un matemático chino que usó lo que conocemos como el Principio de Liu Hui y Zu Geng para calcular el volumen de una esfera. La teoría de Liu-Zu es equivalente al Principio de Cavalieri. Es decir, matemáticos chinos han usado este principio más de mil años antes que Cavalieri. Podemos leer una biografía de Zu Geng en MacTutor y el artículo Zu-Geng's axiom vs Cavalieri's theory de Ji-Huan He.
Una aplicación bien conocida del Principio de Cavalieri nos permite calcular el volumen de una esfera. Podemos comparar el área de una sección de un hemisferio y el área de una sección de un cuerpo que es un cilindro menos un cono. Estas dos áreas son iguales. Entonces los dos cuerpos tienen el mismo volumen. Es fácil calcular el volumen de este segundo cuerpo, y así obtenemos el volumen del hemisferio.

Tenemos que probar que el área del disco es igual al área de la conora circular (para cada sección):
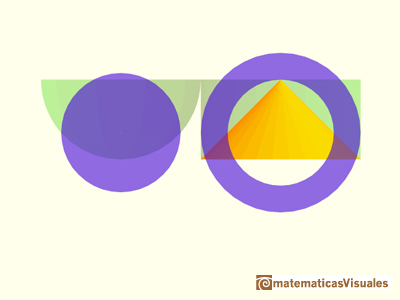
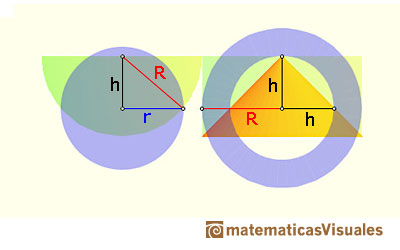
Para cada altura h, el área del disco es:
y el área de la corona circular es:
Por lo tanto, para cada altura las dos secciones tienen áreas iguales.
Usando el Principio de Cavalieri podemos deducir:
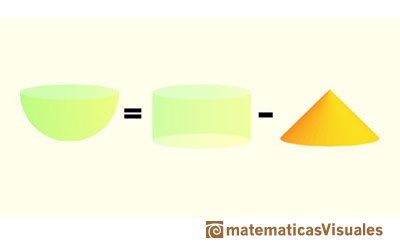
Usando las fórmulas para el volumen de un cilindro y el volumen de un cono podemos escribir el volumen del hemisferio:
Entonces, el volumen de una esfera de radio R es (como Arquímedes ya conocía, 1800 años antes):
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES