Un problema importante relacionado con el origen del Cálculo es encontrar máximos y mínimos de una función. Por ejemplo, Euclides probó que entre todos los rectángulos de igual perímetro, el cuadrado es el que tiene el área mayor. Fermat (que nació en 1601) abordó el problema de un modo diferente y se interesó por la tangente a una curva y la relación de esta tangente con el máximo (o mínimo) de una función. Antes que Fermat, Kepler (1571-1630) fue consciente de esta relación, aunque no en el sentido de funciones y derivadas. Escribió "Nova Stereometria doliorum vinariorum" (1615) un libro sobre el volumen de los barriles de vino y de otros cuerpos.

En esta página intento ilustrar la explicación que hace Otto Toeplitz de este episodio de la Historia del Cálculo ("The Calculus: A genetic Approach" by Otto Toeplitz):
"Junto a sus trabajos astronómicos, un ejemplo de este interés se encuentra en la llamada 'Doliometría', el 'cálculo de barriles'. Cuando él, el astrologo imperial en Linz, se casó por segunda vez, compró vino de un barril para la boda. Para calcular la factura, el mercader de vino midió el barril insertando una regla desde el agujero del tapón S hasta que llega a la tapa en D;
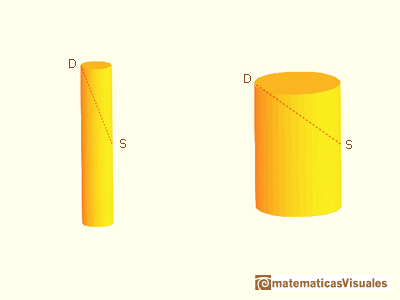
entonces se leyó la longitud SD = d y decidió el precio. Este método enfadó a Kepler, que vio que un barril alto y delgado podría tener la misma distancia SD que uno ancho y que el precio del vino sería el mismo aunque el volumen podría ser mucho menor.
Pensando un poco más en su método de usar d para determinar el volumen, Kepler aproximó el barril por un cilindro, con r el radio de la base y h la altura. Entonces

o
La fórmula general del volumen de un cilindro:
En nuestro caso, sustituyendo r por su valor:
Nos damos cuenta de que el volumen es una función cúbica de la altura del cilindro:
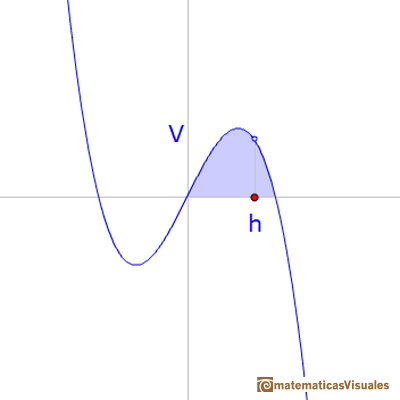
Entonces se pregunta: Si d es fijo, ¿qué valor de h da el mayor volumen V? V es un polinomio en h; por lo tanto la derivada (aunque, desde luego, Kepler no usó derivadas)
Para que V sea un máximo, V' debe ser igual a 0, por lo tanto
Esto definía un barril de una proporciones concretas. Kepler se dio cuenta de que en su Renania natal los barriles eran más estrechos y altos que en Austria, donde su forma era muy parecida a la que da el máximo volumen para d fija -tan cerca que Kepler no creía que pudiera ser accidental. Por lo tanto, imaginó que siglos atrás alguien habia calculado las formas de los barrilles, como él mismo había hecho, y había enseñado a los austríacos a construir sus barriles de este modo particular- un modo muy práctico, desde luego. Kepler mostró que si un barril no satisface exactamente la especificación matemática
pero se desviaba algo de ella, esto tendría poco efecto en el volumen, porque cerca de su máximo una función cambia muy despacio.

Entonces, mientras que este método austríaco de calcular el precio, si se aplica a los barriles renanos sería un fraude, era bastante adecuado para los barriles austríacos. La forma austríaca tenía la ventaja de permitir este método rápido y simple. Kepler se quedó más tranquilo. Trabajando en mejores aproximaciones del volumen de diferentes formas de barriles, consultó a Arquímedes y descubrió que su propio método de indivisibles le había permitido obtener resultados de un modo más simple y general que los de Arquímedes, que había tenido que lidiar con demostraciones difíciles. Lo que él no sospechó es que Arquímedes también había encontrado sus resultados por el mismo método de los indivisibles (¡pues El Método estuvo perdido hasta 1906!). Kepler dedicó a estos problemas un libro entero con cálculos de muchos volúmenes." [Otto Toeplitz]
Puedes leer el libro completo "Nova Stereometria doliorum vinariorum" en The Posner Library.
Podemos ver una página de Nova stereometria doliorum vinaniorum, versión alemana, en MathDL.
En el artículo Kepler: The Volume of a Wine Barrel published by MathDl (Loci, Junio 2010) presenté una versión más completa de esta página en torno a la anécdota que llevó a Kepler a estudiar volúmenes de barriles y otros cuerpos y escribir en 1615 su "Nova Stereometria doliorum vinariorum" (Nueva geometría sólida de los barriles de vino) donde usó algunas técnicas infinitesimales anteriores al descubrimiento del cálculo diferencial e integral por Newton y Leibniz. (En ese artículo algunos mathlets antiguos no funciona bien pero puedes ver aquí una versión completa del artículo 'Kepler: The Volume of a Wine Barrel'). )
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES