Para conmemorar el día internacional de las Matemáticas 2020 se realizó una exposición en el IES Alonso Quijano de Alcalá de Henares sobre el dodecaedro rómbico. Se presenta como un homenaje a Kepler pues él fue el primer matemático que describe este poliedro.
El título de la exposición es "Homenaje a Kepler: las abejas y el dodecaedro rómbico".
Se ha inaugurado el miércoles 11 de Marzo y se mantendrá el tiempo necesario para que se pueda ver bien, teniendo en cuenta la situación actual de pandemia.
En el Boletín 657 de la Real Sociedad Matemática Española se anuncia esta exposición.
Ángel Requena, en su blog "Turismo matemático" hace una muy generosa recomendación de la exposición. Se lo agradezco mucho y es un honor que la exposición comparta un lugar junto a las maravillas que nos muestra y cuenta en su blog.
El proyecto "Homenaje a Kepler: las abejas y el dodecaedro rómbico" ha ganado el concurso convocado en conmemoración del Día internacional de las Matemáticas 2020 en la sección de materiales y recursos didácticos del profesorado. Muchas gracias.
La Sociedad Puig Adam de Profesores de Matemáticas, en su Boletín 111 (Abril 2021), ha publicado un artículo sobre Kepler y el dodecaedro rómbico que puede descargarse aquí.
Quiero agradecer aquí el interés mostrado por todas las personas que están divulgando este proyecto.
Panorámica de la exposición
Esta es la primera parte de la exposición:
Como veremos, la exposición tiene varios objetivos pero el primero de ellos, sin duda, es mostrar la belleza de las Matemáticas y su conexión con la observación de la Naturaleza y los problemas de la vida cotidiana. Todo ello siguiendo el pensamiento de una mente genial y creativa como la de Johannes Kepler.
También queremos mostrar el interés que tiene la construcción y manipulación de poliedros para disfrutar de su belleza y comprender mejor sus propiedades matemáticas. La percepción que se obtiene de ese modo es muy superior.
En este sentido, el centro de la exposición lo forman construcciones hechas uniendo varillas de plástico de colores con vértices fabricados con una impresora 3d. Se quiere explorar esta técnica para la construcción de estructuras complejas. La impresora 3D complementa y amplía las posibilidades de construcción de figuras geométricas. Además se mostrarán otras técnicas, unas más tradicionales como el uso de la cartulina o el origami y otras, quizás menos conocidas, como el recurso de los imanes para mostrar descomposiciones de figuras.
Además queremos que estas construcciones nos cuenten historias. En este caso el hilo conductor es un poliedro que se llama dodecaedro rómbico. Otro protagonista es su creador o inventor que fue Johannes Kepler pues intentaremos seguir su mente creativa por varios caminos que le llevan a este poliedro rómbico.
La exposición tiene dos partes. La primera es más sencilla e intuitiva y en ella se quiere mostrar cómo Kepler se inspira en la Naturaleza y relaciona fenómenos naturales con problemas prácticos para concebir el dodecaedro rómbico. Veremos aquí dos caminos. En el primero de ellos las abejas juegan un papel fundamental.
La segunda parte es profunda aunque no complicada. Se muestra aquí cómo el concepto de dualidad nos ofrece otro punto de vista que lleva a Kepler más lejos, inventando un segundo poliedro rómbico. Además presentará al cubo como el tercer poliedro rómbico.
PARA SABER MÁS
Para saber más sobre Kepler como matemático puedes seguir el siguiente enlace en el que se aborda un asunto más complicado que el que estamos trabajando en esta página sobre poliedros. Allí se muestra cómo Kepler, una vez más, aprovecha un incidente de su vida cotidiana, en este caso su boda, para abordar el problema matemático del cálculo de volúmenes. Junto con Arquímedes (y otros), Kepler es un precursor del cálculo integral.
Kepler también fue astrónomo, seguidor de las teorías de Copérnico. Es conocido por sus "tres leyes de Kepler" en las que describe el movimiento de los planetas alrededor del sol. Newton vendría después.
Para empezar la primera parte nos fijamos en el poliedro protagonista que es el dodecaedro rómbico. Tiene 12 caras que son rombos iguales.
Este sería un ejemplo de construcción de este poliedro con cartulina:
Y con origami:
Podríamos pensar que este poliedro está relacionado con el sólido platónico de doce caras, el dodecaedro, pues ambos tienen el mismo número de caras. Sin embargo, está mucho más relacionado con el cubo. Es bueno notar, como luego veremos, la importancia de que el cubo tiene 12 aristas.
Esta relación con el cubo nos va a llevar a la sorprendente propiedad del dodecaedro rómbico de teselar el espacio, al igual que hace el cubo.
Teselar el espacio con un poliedro quiere decir que con copias de ese poliedro podemos rellenar el espacio sin dejar huecos.
El cubo (y todos los poliedros que llamamos ortoedros y también los paralelepípedos) tienen esta propiedad que nos resulta muy familiar. Basta pensar en los almacenes llenos de cajas apiladas, los ladrillos y un largo etcétera.
De hecho, el cubo es el único poliedro regular que cumple esta importante propiedad. Una consecuencia de este hecho es que usamos cubos para definir las unidades de volumen.
Aquí vemos un detalle de la construcción en la que podemos ver cómo los cubos teselan el espacio.
Teselar el espacio es lo análogo, en dimensión tres, de lo que llamamos mosaicos en el plano, o dimensión 2. La palabra tesela se refiere a cada una de las piezas de un mosaico.
El ejemplo más sencillo de mosaico plano es el formado por cuadrados. Así es como termina nuestra construcción.
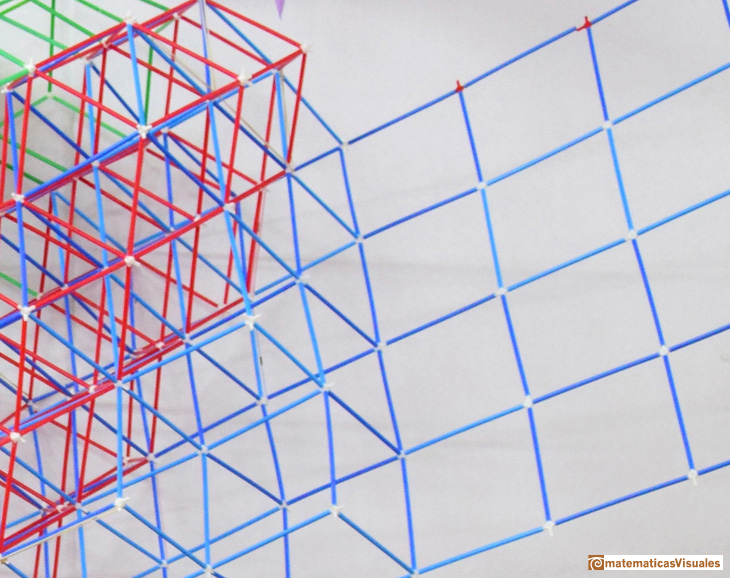
Por lo tanto, uno de nuestros objetivos es mostrar cómo esa relación entre el dodecaedro rómbico y el cubo nos ayuda a explicar la sorprendente propiedad del dodecaedro rómbico de teselar el espacio.
¿Cómo llega Kepler a descubrir este poliedro y a comprender sus propiedades? Vamos a ver que se inspira en la Naturaleza y lo relaciona con otros problemas.
Ya hemos comentado que el primero que describe este poliedro es Johannes Kepler, en torno a 1600. Lo hace en un librito maravilloso que se titula en latín "De Nive Sexangula", algo así como "El cristal de nieve de seis puntas"
Esta es una edición en latín e inglés. Las ilustraciones de esta edición las ha hecho una matemática española que se llama Capi Corrales Rodrigáñez.
Hay traducción castellana titulada "Regalo de año nuevo, sobre el copo de nieve hexagonal;Strena seu de nive sexangula". Fue realizada por Ana García Azcárate y Ángel Requena Fraile y editada por la editorial Avinareta. La información me la ha proporcionado Ángel Requena que es el autor del excelente blog Turismo matemático.
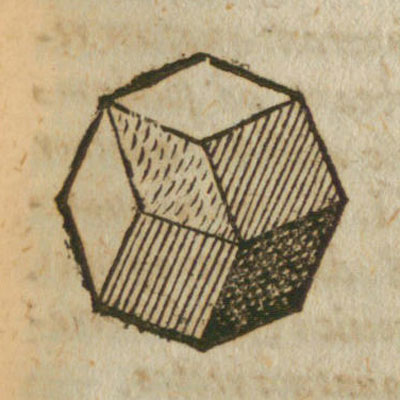
Es sorprendente que este poliedro no se describiera antes pues de modo natural el granate se nos presenta como un dodecaedro rómbico. Aprovechamos para recordar que los geólogos (en sus estudios de Cristalografía) están muy interesados en los poliedros.
Es interesante ver las relaciones que establece Kepler entre el dodecaedro rómbico y otros problemas que le interesan. Por ejemplo, piensa sobre cómo se apilan las balas de cañón para ocupar menos espacio.
Una esfera así apilada está en contacto con seis vecinas en su mismo plano, con tres que hay encima y con tres por debajo. En total, con doce.
Si esas esferas fueran deformables y se comprimieran de un modo homogéneo se deformarían en un poliedro con 12 caras que resultaría ser el dodecaedro rómbico.
Entonces observa que los granos de la granada, que han crecido y se han comprimido entre ellos, tienen caras romboidales.
KEPLER Y LAS BALAS DE CAÑÓN
Este es un tema muy interesante y pensé en hacer un experimento para comprobar este resultado.
Resultó se fácil y espectacular. He preparado una página para mostrar el resultado y cómo hacerlo.
Kepler también se fija en los panales de las abejas y esa es la relación que queremos destacar aquí.
La primera construcción de la exposición, que ya hemos visto que termina con un mosaico formado por cuadrados, empieza con los otros dos mosaicos planos que se pueden hacer con polígonos regulares: el mosaico formado por triángulos equiláteros y el formado por hexágonos.
Lo primero que llama la atención al observar un panal de abejas es su estrutura de mosaico hexagonal.
El matemático Pappus de Alejandría ya había escrito sobre ese plan hexagonal de los panales planteando la posibilidad de que las abejas tuvieran "cierta previsión geométrica". Escribió: "Habiendo, pues, tres figuras que por sí mismas pueden llenar el espacio alrededor de un punto, verbigracia, el triángulo, el cuadrado y el hexágono, las abejas han seleccionado sabiamente la estructura que contenía más ángulos, sospechando que en realidad podrían contener más miel que cualquiera de las otras dos". (Citado por D'Arcy Thompson)
Kepler va más allá y se fija en cómo las abejas cierran sus celdillas. Es el primero en describirlo. En la base de las celdas la estructura hexagonal se deforma para cerrarse. Y lo hace con tres rombos iguales especiales.
En nuestra exposición mostramos cómo se produce esa deformación y cierre con tres rombos:
Sobre esta base las abejas construyen sus celdillas. En estos tres marcos de colmenas se ve el proceso de construcción de las celdillas por las abejas en tres fases diferentes, desde la base a las celdas completas.
Así se muestran en nuestro montaje:
Las abejas generan dos capas de celdillas
PARA SABER MÁS
Para explorar la forma de los panales de abeja puedes visitar esta página. La aplicación interactiva requiere el pluging de Flash.
La siguiente página es un poco más complicada. Nos planteamos un problema de optimización: ¿cómo pueden cerrarse las celdas de un panal de abejas usando tres rombos iguales de modo que su superficie sea mínima?. Para resolver un problema de optimización de este tipo definimos una función y usamos su derivada para obtener un mínimo. En esta página se muestra cómo una determinada configuración geométrica se relaciona con una función con la que podemos trabajar. Modificando la configuración nos vamos moviendo por distintos valores de la gráfica y podemos entender bien el problema.
Kepler comprende que con esos rombos especiales se puede construir un poliedro de doce caras. Ese es el dodecaedro rómbico. El procedimiento no es complicado: partiendo de los tres rombos de la base de la celda se añaden seis rombos, uno en cada pared de la celda. Ya tenemos nueve rombos. Se cierra el poliedro con otros tres rombos.
Si pensamos en las balas de cañón apiladas podemos pensar que los tres primeros rombos corresponden con las tres vecinas que tiene una bola por debajo, los seis rombos de las paredes se corresponden con las seis bolas con las que está en contacto en su plano y los tres últimos rombos se relacionan con las tres bolas que hay por encima.
Esta manera de llegar al dodecaedro rómbico a partir de los panales de las abejas es muy sugestiva y nos habla de la capacidad de observación e intuición de Kepler. Relaciona el estudio de las formas de la Naturaleza con las Matemáticas y lo conecta con el problema práctico del almacenamiento de bolas de cañón. Una maravilla y un placer seguir el hilo del pensamiento de Kepler.
Sin embargo, hay otra manera de describir este poliedro mucho más sencilla también conocida por Kepler.
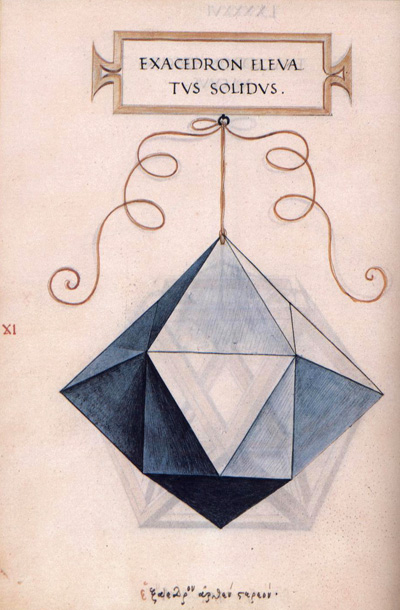
Se trata de ver este poliedro partiendo de un cubo al que se le añaden seis pirámides en cada una de sus caras. Este procedimiento de generar nuevos poliedros era conocido desde antiguo. En particular Luca Pacioli y Leonardo da Vinci lo describen y podemos ver lo cerca que estuvieron del descubrimiento de este poliedro en esta imagen del libro "La Divina Proporción" de Luca Pacioli con ilustraciones de Leonardo:
Si a un cubo le añadimos estas pirámides resulta un poliedro con 24 caras. Pero, para una determinada altura de esas pirámides, pares de caras triangulares adyacentes están en el mismo plano y podemos decir que se funden en una sola cara romboidal sobre cada una de las doce aristas del cubo.
Así se genera el dodecaedro rómbico.
De esta manera podemos comprender mejor cómo son los rombos de sus caras, sus proporciones. También podremos calcular con facilidad el volumen de este poliedro. Además se deduce la interesante relación entre las proporciones de estos rombos y las de una hoja de papel DinA4.
PARA SABER MÁS
Con la aplicación interactiva podrás ver posibilidades de añadir pirámides a un cubo.
El caso que nos interesa es el del dodecaedro rómbico. A partir de esta construcción se puede calcular la proporción de las diagonales de los rombos y los ángulos en sus vértices.
Curiosamente, la proporción entre las diagonales de esos rombos están relacionada con las dimensiones de un folio (DinA4). Con una hoja de papel podemos doblar uno de estos rombos con mucha facilidad. ¿Sabes cómo?.
También podemos calcular su volumen, como se muestra en esta página:
Además, de este modo vemos con claridad que el dodecaedro rómbico tesela el espacio.
Así es como lo describe Steinhaus en su libro "Instantáneas matemáticas":
Hugo Steinhaus escribió: "Ya hemos mencionado el teselamiento de todo el espacio con cubos. Podemos obtener otro teselado de este tipo con el siguiente procedimiento: hacemos los cubos alternativamente blancos y negros para obtener una especie de tablero de ajedrez y quitamos los cubos negros. Descomponemos cada uno de estos espacios vaciós en seis pirámides de base cuadrada con un vértice común en el centro del espacio vacío. Si consideramos un solo cubo blanco con 6 pirámides con sus bases en él podemos ver un dodecaedro rómbico con un cubo inscrito en él. Es obvio que con esta procedimiento hemos rellenado todo el espacio con dodecaedros rómbicos congruentes." (Steinhaus, pag. 185)
PARA SABER MÁS
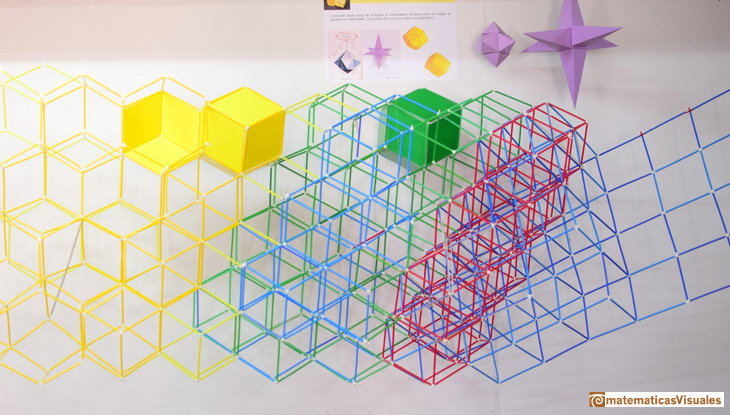
Así muestra nuestra construcción esta combinación de teselación del espacio por cubos y por dodecaedros rómbicos.
La teselación con cubos se transforma en un mosaico plano formado por cuadrados.
Podemos considerar ahora cumplido el primer objetivo que ha sido la presentación del poliedro que llamamos dodecaedro rómbico, en la que hemos visto cómo Kepler relaciona este poliedro con fenómenos de la Naturaleza. También hemos podido plantearnos el estudio de sus medidas, la proporción de sus caras y su volumen.
Además hemos podido justificar la sorprendente propiedad de este poliedro de teselar el espacio a partir de su relación con el cubo.
Es muy conveniente construir y manipular este poliedro para comprenderlo mejor.
Estos son los modelos que se pueden descargar:
OTRAS ACTIVIDADES
Estudio y dibujo de mosaicos. Mosaicos en nuestra vida cotidiana (embaldosados, etc.) y en el Arte (mosaicos en el arte musulmán, Escher).
Vida de las abejas. Los panales. Peligros que padecen las abejas en el mundo actual.
Otros poliedros que teselan el espacio. Uno de ellos es un poliedro arquimediano: el octaedro truncado. Se puede estudiar la relación de este poliedro con el cubo que tiene como consecuencia la propiedad de teselar el espacio.
Esta es la segunda parte de la exposición:
En la segunda parte de la exposición se quiere mostrar otra faceta complementaria y profunda de la mente matemática de Kepler.
En su estudio de los poliedros (y también en sus trabajos sobre el cálculo de volúmenes) Kepler retoma el testigo de Arquímedes y lo profundiza. En sus trabajos se inspira en los solidos platónicos, los más regulares, y también describe los poliedros arquimedianos (que estaban un poco olvidados).
SI HAY QUE REPASAR
Aquí puedes ver una descripción de los cinco sólidos platónicos:
De los poliedros han interesado sus medidas: longitudes, áreas y volúmenes. Pero en el momento en que se considera que los vértices, las aristas y las caras son elementos esenciales de los poliedros se está dando un salto importante. Es decir, nos fijamos en los elementos de dimensión cero (puntos, vértices), dimensión uno (rectas, segmentos, aristas) y dimensión dos (planos, caras). La primera consecuencia de contar estos elementos nos lleva a la idea de que los poliedros forman parejas. Es lo que llamamos dualidad. Kepler era plenamente consciente de esta noción de dualidad (aunque no usa esta palabra). Una segunda consecuencia será la fórmula de Euler para los poliedros que enuncia Euler unos 150 años después. Estamos hablando de los orígenes de una rama de las Matemáticas llamada Topología.
El concepto de dualidad empareja poliedros que tienen el mismo número de aristas pero que intercambian el número de caras y de vértices.
Si aplicamos esta idea a los poliedros platónicos vemos que el cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro se empareja con él mismo (decimos que es autodual).
Kepler conoce este emparejamiento entre poliedros.
SI HAY QUE REPASAR
Para ver el concepto de dualidad referido a los sólidos platónicos puedes seguir el siguiente enlace. Allí verás ejemplos de estas parejas de poliedros con construcciones que se han hecho con diferentes técnicas.
Hay dos modos de colocar estas parejas de poliedros duales.
Si nos fijamos en que intercambian vértices y caras se puede colocar uno dentro de su pareja con los vértices del interior en los centros de las caras del otro. Así se puede colocar un cubo dentro de un octaedro o un octaedro dentro de un cubo.
Si nos fijamos en que tienen el mismo número de aristas podemos colocar estas parejas de poliedros de modo que sus aristas se bisequen ortogonalmente y obtenemos nuevos poliedros. Decimos que esa pareja de poliedros están en posición recíproca.
Si pensamos en el cubo y el octaedro en posición recíproca, uniendo adecuadamente los vértices obtenemos un poliedro que los envuelve que resulta ser el dodecaedro rómbico.
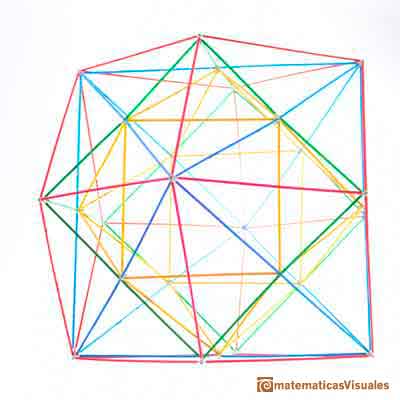
Aquí vemos el cubo y el octaedro en posición recíproca y, a los lados, un cubo y un octaedro dentro de un dodecaedro rómbico.
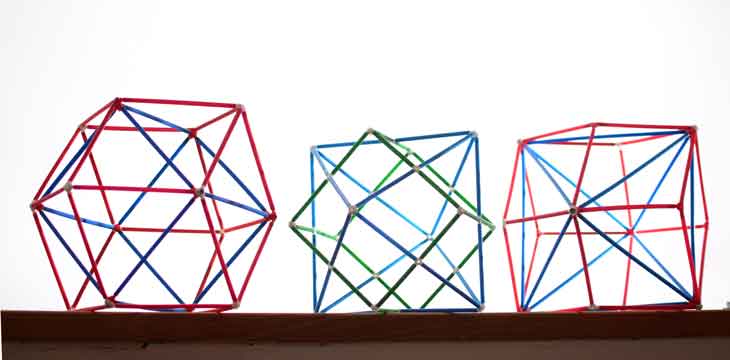
Es interesante ver que la parte común, la intersección de ambos poliedros, es otro poliedro que es el cuboctaedro.
Este poliedro está formado por cuadrados y triángulos equiláteros y pertecene a la familia de los poliedros de Arquímedes.
Resulta que el dodecaedro rómbico y el cuboctaedro son poliedros duales. (Los poliedros duales de los poliedros de Arquímedes se llaman poiedros de Catalan. Por lo tanto, el dodecaedro rómbico es un poliedro de Catalan).
En esta construcción, realizada con la impresora 3D podemos ver el cubo (verde) y el octaedro (azul) en posición recíproca. La envoltura es el dodecaedro rómbico (rojo) y en el interior está el cuboctaedro (amarillo).
PARA SABER MÁS
Una vez que ha obtenido el dodecaedro rómbico de esta manera, Kepler va más allá y aplica un principio fundamental de las Matemáticas y de la Ciencia en general. Considerar la idea en una situación análoga. Aplica la técnica a otrar pareja de poliedros duales que es la formada por el icosaedro y el dodecaedro. El resultado es que descubre un segundo nuevo poliedro rómbico.
La envoltura de la construcción del icosaedro y el dodecaedro en posición recíproca es un poliedro de 30 caras rómbicas que se llama triacontaedro.
Notamos que estos rombos son distintos a los del dodecaedro. Estos están relacionados con la proporción aúrea. En el interior, la intersección, es el icosidodecaedro, formado por pentágonos y triángulos. Es un sólido de Arquímedes. El triacontaedro es su dual y, por lo tanto, también es un sólido de Catalan.
Este es el triacontaedro construido con Zome. Es su interior hay un icosidodecaedro de cartulina. Se muestra la dualidad de ambos poliedros.
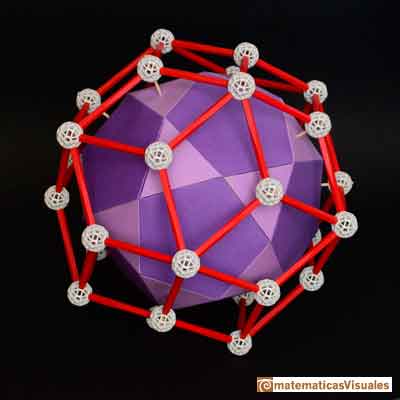
En esta construcción podemos ver el dodecaedro (blanco) y el icosaedro (azul) en posición recíproca. En el interior, el icosidodecaedro (amarillo) y el exterior, el triacontaedro (rojo).
No es fácil ver estos poliedros en una fotografía pero en realidad es mucho más sencillo e instructivo.
Aplicando esta idea al tetraedro y poniendo dos tetraedros en posición recíproca obtenemos como poliedro, la stella octangula. Este bonito poliedro ya era conocido con anterioridad a Kepler. Leonardo lo dibuja para el libro "La divina proporción" de su amigo Luca Pacioli. Es Kepler el que lo bautiza con el nombre stella octangula, estrella de ocho puntas. Si, como en los casos anteriores, consideramos su envoltura externa lo que obtenemos es un cubo. Aunque ya es un viejo conocido, aquí lo vemos como el tercer poliedro rómbico (sus caras son cuadrados, es decir, rombos que son rectángulos). En su interior encontramos un octaedro que, como sabemos, es dual del cubo.
Esta es la construcción con los vértices hechos con la impresora 3D. Cuando tenemos esta construcción en nuestras manos podemos ver dos tetraedros en posición recíproca formando la stella octangula (en rojo), en su interior, el octaedro (amarillo) y como envoltura exterior, el cubo (verde).
PARA SABER MÁS
Como en todos los casos en los que hacemos una construcción tridimensional obtenemos un placer estético diferente al de contemplar una representación plana.
UN RESUMEN
Hemos querido mostrar pues el interés en construir poliedros para comprenderlos y disfrutar de su belleza que es la belleza de las Matemáticas.
Exploramos posibilidades de una herramienta que es la impresora 3D que complementa y amplía otras técnicas más tradicionales. Esa herramienta está al alcance de muchos de nosotros.
Hemos seguido el pensamiento de Kepler por diferentes caminos que le han llevado al descubrimiento de un nuevo poliedro rómbico que es el dodecadedro rómbico. Y lo ha hecho a partir de la observación de la Naturaleza y su relación con problemas prácticos.
En un modo de ver la génesis de este poliedro, las abejas han jugado un papel fascinante.
Estudiando la relación de este poliedro con el cubo comprendemos mejor sus propiedades, en particular, una muy interesante que es que este poliedro tesela el espacio.
En un proceso de abstracción notable, Kepler relaciona este poliedro con el concepto de dualidad. Descubre un segundo poliedro rómbico con 30 caras y reconoce al cubo como tercer poliedro rómbico.
Estas son las historias, muy bonitas por cierto, que nos cuentan estas estructuras.
UNAS NOTAS SOBRE LA CONSTRUCCIÓN DE LA EXPOSICIÓN
Como en todos los casos en los que hacemos una construcción tridimensional obtenemos un placer estético diferente al de contemplar una representación plana.
La comprensión del objeto construído, en este caso, un poliedro es muy superior.
Si la estructura es compleja todavía es mayor la diferencia.
El uso de la impresora 3D nos permite explorar otra técnica de construcción de poliedros. En esta ocasión se explora la construcción de una estructura grande a partir de elementos pequeños impresos. Los vértices impresos son unidos por varillas de plástico de colores. Las posibilidades constructivas son inmensas.
Esta técnica se centra en los vértices y las aristas. Podemos decir que otras técnicas se centran en las caras (construcción de poliedros a partir de su desarrollo o uniendo caras de cartulina con pegamento o gomas).
En el caso del dodecaedro rómbico nos fijamos que necesitamos vértices de dos tipos pues hay unos en los que se unen tres caras y otros en los que se unen cuatro.
El diseño se ha realizado con OpenSCAD y estos son los vértices de los dos tipos:
Si queremos hacer la teselación necesitamos estos vértices:
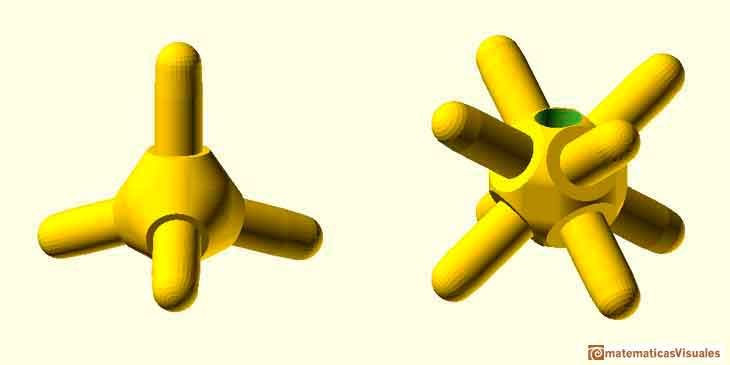
Para completar la construcción se necesitan vértices de otros tipos que serán descritos en otra página: vértices para las celdas hexagonales, para el mosaico hexagonal, para los cubos dentro del dodecaedro, etc...
REFERENCIAS
SIGUIENTE
ANTERIOR
MÁS ENLACES
