El octaedro tiene una estelación que es el octaedro estrellado.
Fue dibujado por Leonardo da Vinci para el libro de Luca Pacioli 'La divina proporción' en 1509.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).
Cien años después, Johannes Kepler lo llamó 'Stella octangula'.
Puede verse como el poliedro compuesto por dos tetraedros (un tetraedro y su dual, un segundo tetraedro).
Los ocho vértices son los vértices de un cubo.
Esta estelación está formada por un octaedro con tetraedros en cada cara.
Es fácil calcular el volumen del octaedro estrellado si conocemos el volumen de un octaedro
y el volumen de un tetraedro.
Entonces el volumen de un octaedro estrellado o stella octangula de lado a es:
Vamos a ver un poco más el concepto de dualidad de poliedros.
Los elementos principales de un poliedro son los vértices, las aristas y las caras. Por ejemplo, un tetraedro tiene
cuatro vértices, seis aristas y cuatro caras (elementos de dimensión 0, 1 y 2 respectivamente).
El dual (o recíproco) de un poliedro es un poliedro que tiene el mismo número de aristas que el original pero
que tiene cambiados el número de caras y vértices.(Wenninger)
Por ejemplo, el cubo y el octaedro son poliedros duales. Un cubo tiene ocho vértices y seis caras y
un octaedro tiene ocho caras y seis vértices. Ambos tienen doce aristas.
En el caso del tetraedro, tiene cuatro vértices y cuatro caras. Por lo tanto, el dual de un tetraedro es otro tetraedro.
Decimos que el tetraedro es autodual.
A partir de un poliedro regular podemos construir el dual considerando el circuncentro de cada cara y conectando puntos
de caras adyacentes. Estas aristas son las aristas del poliedro dual.
¿Cuál es el tamaño relativo de estos dos tetraedros?
Otra manera interesante de construir el dual de un sólido platónico o arquimediano es modificar los tamaños de modo
que las respectivas aristas de un poliedro y su dual sean perpendiculares y se bisequen.
De este modo se forma un poliedro compuesto.
En el caso del tetraedro, el tetraedo y su dual o recíproco forma un compuesto de dos tetraedros que es la Stella octangula
de Kepler.
Como ya hemos visto, el sólido común a ambos tetraedros es un octaedro.
Estos dos tetraedros están contenidos en un cubo. Resulta que el cubo y el octaedro son poliedros duales.
Las aristas de la Stella octangula son las diagonales de las caras de un cubo y se cruzan dos a dos en los vértices del
octaedro. (Cundy, p. 129)
Podemos considerar que la Stella octangula tiene ocho caras que estan en los planos de las caras del octaedro.
Es decir, que la Stella octangula es estellación de un octaedro.
Detalle en una casa del Museo al Aire Libre de la Selva Negra (cerca de Gutach, Alemania)
REFERENCIAS
Hugo Steinhaus, Instantáneas matemáticas (pags. 187-192),Editorial Salvat (1986)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Magnus Wenninger - 'Dual Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
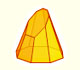
Desarrollos planos de pirámides truncadas por un plano oblicuo.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
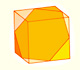
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
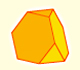
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
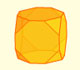
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.








 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR











































