
Pirámides cortadas por un plano oblicuo
En desarrollos planos de cuerpos geométricos (5): Pirámides y troncos de pirámide hemos visto pirámides y pirámides truncadas por un plano paralelo a la base. En esta página podemos estudiar pirámides truncadas por un plano oblicuo y cómo se pueden desarrollar en una red o desarrollo plano.
Hemos visto casos similares de figuras cortadas por planos oblicuos en desarrollos planos de cuerpos geométricos (2): Prismas cortados por un plano oblicuo y en desarrollos planos de cuerpos geométricos (4): Cilindros cortados por un plano oblicuo.
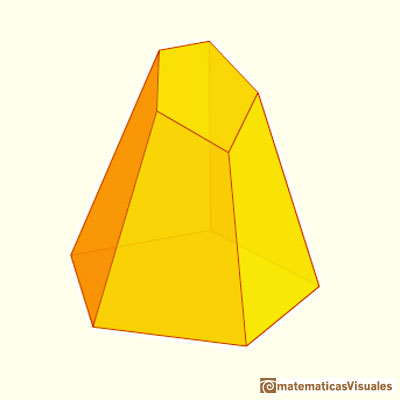


Otro ejemplo:

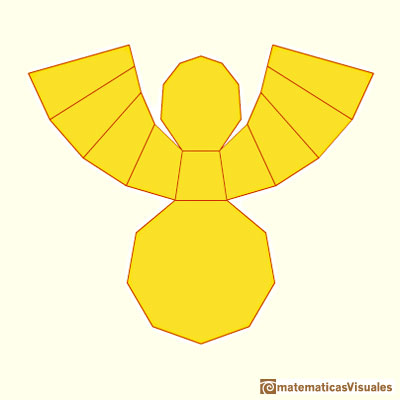
Cuando la pirámide tiene muchas caras es, de alguna manera, semejante a un cono y la sección oblicua se parece a una elipse:
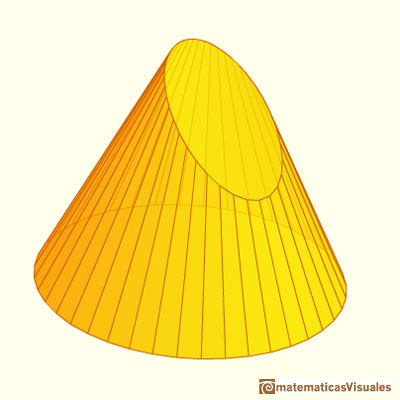
 ANTERIOR
ANTERIOR
MÁS ENLACES

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.













 SIGUIENTE
SIGUIENTE




