El octaedro regular es un poliedro que tiene ocho caras que son triángulos equiláteros, seis vértices y doce
aristas.
Es un sólido de los llamados platónicos y es bien conocido desde la Antigüedad.

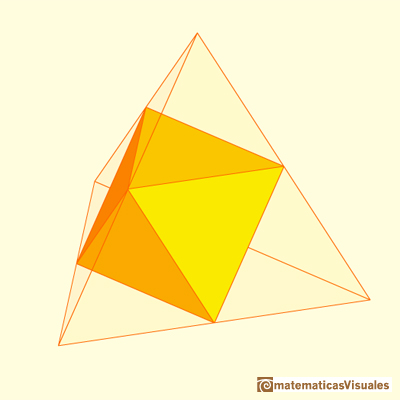
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
Leonardo da Vinci dibujó dos octaedros para el libro de Luca Pacioli 'De Divina Proportione'
(pubicado en 1509).

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.
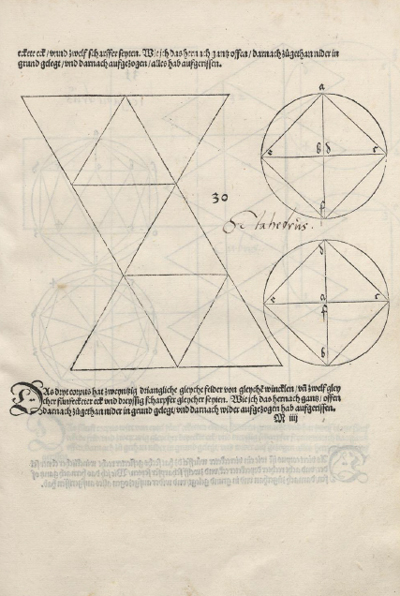
Pero fue Durero el primero en publicar desarrollos planos de poliedros. En su libro
'Underweysung der Messung' ('Cuatro Libros de la Medida', publicado en 1525) el autor dibujó desarrollos planos de los cinco sólidos platónicos y de otros poliedros
(entre ellos, varios sólidos arquimedianos).
Por ejemplo, este octaedro regular:
"El que Durero estuviera o no al corriente del trabajo de los dos italianos especialistas en este campo, Luca Pacioli
y Piero della Frascesca, es una cuestión abierta. Lo cierto es que (...) abordó el problema de una manera completamente independiente. Pacioli
(...) los ilustró [varios poliedros] con imágenes en perspectiva o estereográficas. Durero trató (...)[más poliedros] y, en lugar de representar
estos sólidos en perspectiva o con imágenes estereográficas, ideó un método original y, se puede decir
proto-topológico, desarrollándolos en una superficie plana de modo que sus caras formen una 'red' coherente la cual,
cuando la cortamos en papel y la plegamos y unimos adecuadamente sus caras, formará un modelo tridimensional del sólido en cuestión."
(Panofsky, p.259)
Jugando con la aplicación interactiva podemos ver cómo el octaedro se transforma en su desarrollo plano.
Podemos descargarnos el desarrollo de un octaedro y construir con cartulina nuestra figura.
INVESTIGA
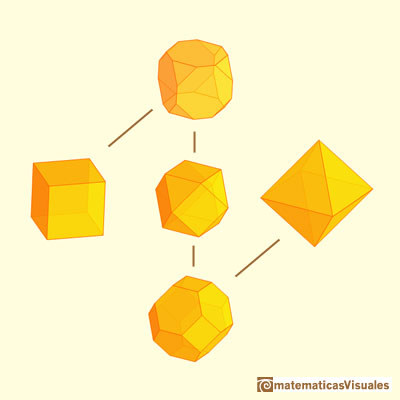
El octaedro está relacionado con otros poliedros.
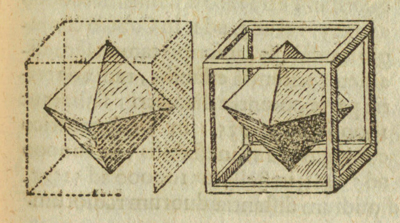
El octaedro y el cubo son poliedros duales:
Kepler dibujó un octaedro dentro de un cubo mostrando que las caras de uno de estos poliedros se corresponden con los vértices del otro.
El cubo y el octaedro se pueden colocar en lo que llamamos 'posición recíproca'. La figura formada es una estelación del cuboctaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
La estelación del octaedro es el poliedro que Kepler llamó 'Stella Octangula':

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
Si truncamos adecuadamente un octaedro obtenemos un sólido arquimediano que tiene propiedades muy interesantes:

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
Podemos obtener un octaedro truncando un tetraedro:
REFERENCIAS
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Erwin Panofsky - The Life and Art of Albrecht Dürer - Princeton University Press
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press (p. 76)
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.
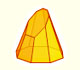
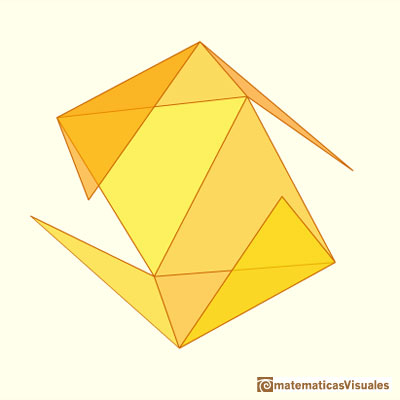
Desarrollos planos de pirámides truncadas por un plano oblicuo.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.




















 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR













































