Tetraedro:
Cubo:
Octaedro:
Icosaedro:
Dodecaedro:
INVESTIGA
¿Por qué la unión de dos tetraedros no es un sólido platónico?
El cubo, el octaedro, el tetraedro y otros poliedros
Taller de Talento Matemático (Zaragoza) 2014-2015
Sesión del Taller de Talento Matemático de Zaragoza por Roberto Cardil.
Viernes día 7 de Noviembre de 2014 a las 18:15.
Objetivos:
Como en ocasiones anteriores, el principal objetivo es pasar un buen rato hablando de algunos poliedros. Empezando por la familia más regular, la de los sólidos platónicos.
También queremos animar a la construcción de poliedros con diferentes técnicas sencillas (papiroflexia, cartulina, tubos, gomas, Zome, etc.).
Estas construcciones son muy bonitas y obtenemos un placer estético al verlas y tocarlas. También nos ayudan a desarrollar nuestra percepción espacial.
Pero en esta sesión me quiero centrar en el hecho de que la construcción de estos cuerpos geométricos nos ayudan a razonar y a obtener conclusiones matemáticas. Es decir, nos ayudan a pensar.
Veremos cómo podemos calcular, de un modo sencillo, el volumen del octaedro y el del tetraedro. Primero usaremos la conocida fórmula del volumen de las pirámides.
Esta fórmula general no es tan sencilla de probar. Nos podemos plantear si se puede deducir el cálculo del volumen del octaedro y del tetraedro sin recurrir a ella y veremos que sí. Que es sencillo a partir de construcciones de poliedros. Para ello nos adentraremos un poco más en el mundo de los poliedros y conoceremos un elemento de otra familia de poliedros muy importante, los sólidos arquimedianos. Con su ayuda podremos calcular el volumen del octaedro.
Tendremos que hacer una construcción, para cogerle gusto. Necesitaremos tijera, regla y pegamento. También papel y lápiz, para hacer alguna cuenta.
Todos aquellos que tengan algún poliedro en casa pueden traerlo a la sesión para que todos nos animemos a construir cuerpos geométricos, porque son elegantes y nos enseñan a pensar.
Esta sesión tiene un espíritu parecido a la sesión del Taller de Talento Matemático realizada el 13 de Abril de 2012.
Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.
Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
1.- Los cinco sólidos platónicos
2.- Áreas y volúmenes de figuras semejantes
Cuando queremos estudiar una figura nos solemos fijar en una de sus dimensiones. En el caso de los cuadrados, y en el de los polígonos regulares en general, es bastante habitual fijarse en el lado.
Otras dimensiones de la figura, como su diagonal, dependen del lado. Éste es un cuadrado de lado 1.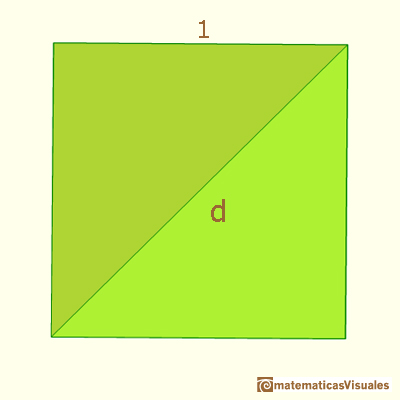
La longitud de la diagonal de un cuadrado depende de la longitud del lado. Podemos escribir la longitud de la diagonal de un cuadrado de lado 1 de un modo muy compacto:
El área de un cuadrado también depende de sus dimensiones, desde luego. Nos fijamos en el lado y podemos escribir de un modo muy compacto el área de un cuadrado de lado 1:
Este cuadrado tiene diagonal 1, ¿cuál es su lado?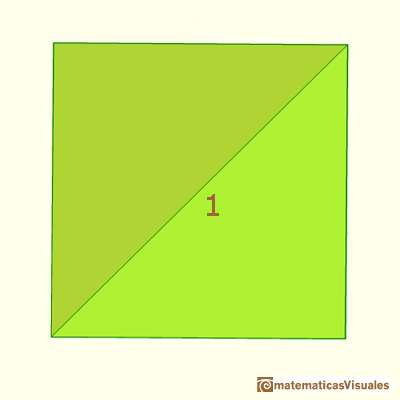
Así podemos escribir su área:
Este cuadrado es más grande. Su diagonal es 2. Podemos calcular el valor del lado:
El área de este cuadrado la escribimos:
Y su valor es fácil de calcular
En general se verifica esta fórmula para las áreas de los cuadrados
No es necesario que sean cuadrados. Para dos figuras semejantes el área cumple esta importante propiedad.
La propiedad anterior se refiere a las áreas. La podemos ver como una generalización de lo que ocurre con distancias correspondientes en dos figuras semejantes que han sido ampliadas o reducidas por un factor a. Por ejemplo, la altura de un triángulo o la diagonal de un polígono en relación con el mismo segmento de la misma figura ampliada o reducida.
Lo podemos expresar así, donde L representa la longitud de una determinado segmento:
Usando esta notación podemos mecanizar muchos cálculos.
En muchas de estas cuestiones tenemos que utilizar el teorema de Pitágoras para calcular el valor de la diagonal o el de una altura. Pero en algunas situaciones basta hacerlo una sola vez para un caso particular y después aplicar las propiedades de la semejanza.
Por ejemplo, para calcular la altura y el área de un triángulo equilátero podemos elegir el caso que más nos convenga, el más sencillo. Para calcular la altura (que depende del tamaño del lado) de un triángulo equilátero usaremos el teorema de Pitágoras.
¿Cuál es un buen triángulo para hacer esto cálculos?¿Cuál es preferible, el de lado 1 o el de lado 2?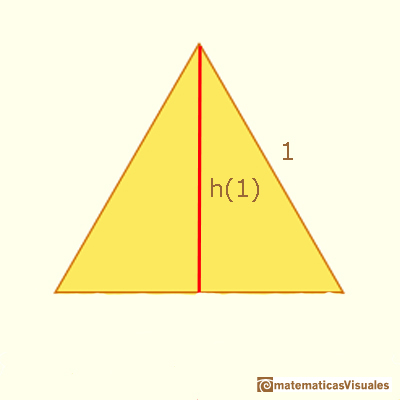
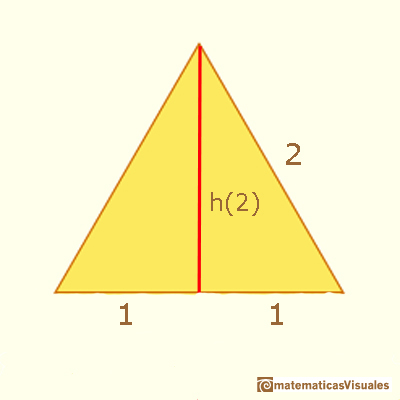
Entonces, la altura de un triángulo de lado 1 es:
El área de un triángulo equilátero de lado 2 es muy sencilla:
Se verifica la relación con el de lado 1:
Por lo tanto, el área de un triángulo de lado 1 es:
Se verifica la fórmula general del área de figuras semejantes:
INVESTIGA
Johnatan Swift escribió 'Los viajes de Gulliver'. En uno de sus viajes llega al país de Liliput que son enanos desde el punto de vista de Gulliver. Gulliver es 12 veces más alto. Los matemáticos liliputienses tienen claro cuántas capas liliputienses hacen falta para hacerle una capa a Gulliver.
¿Sabrías hacer este cálculo y escribirlos con la notación que estamos usando?
Hemos visto que las longitudes y las áreas de figuras semejantes tienen una propiedad análoga.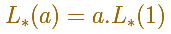
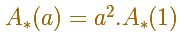
Vamos a ver que en el caso de figuras semejantes también se cumple una propiedad que nos va a ayudar a calcular volúmenes. Empezamos estudiando el cubo.
3.- El cubo y su volumen
El cubo tiene interesantes propiedades:
1) Es el único sólido platónico que rellena el espacio. A veces, decimos que 'tesela' el espacio. Transformaciones de esta figura también rellenan el espacio, como pueden ser las cajas (que por eso se emplean en la paquetería). Son los ortoedros. Los paralelepípedos también teselan el espacio.
2) Usamos el cubo como unidad de medida de volumen.
El volumen del cubo de diagonal 1 lo podemos escribir (en función de su arista)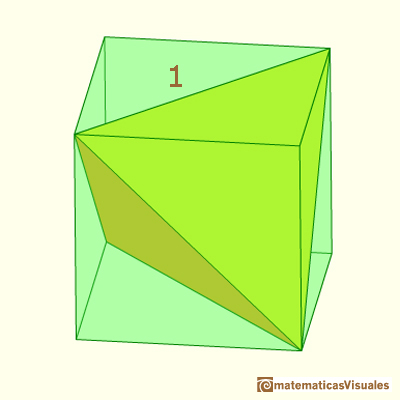
Podemos calcular ese volumen
El volumen de un cubo con diagonal de la cara igual a 2:
Para el volumen de cubos se cumple
No es necesario que sea un cubo. Esta relación se cumple para el volumen de figuras semejantes:
INVESTIGA
Gulliver es 12 veces más alto que un liliputiense. Los matemáticos liliputienses tienen claro cuántas raciones necesitan para darle de beber y de comer.
¿Sabrías hacer este cálculo y escribirlo con la notación que estamos usando?
Hemos visto que los volúmenes de figuras semejantes cumplen una propiedad análoga a la de las longitudes y las áreas.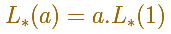
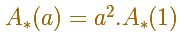
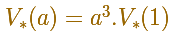
4.- Sección hexagonal del cubo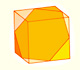
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
La intersección de un cubo por un plano perpendicular a una de sus diagonales por su centro es un hexágono regular. Este plano divide al cubo en dos mitades.
El volumen de este medio cubo es: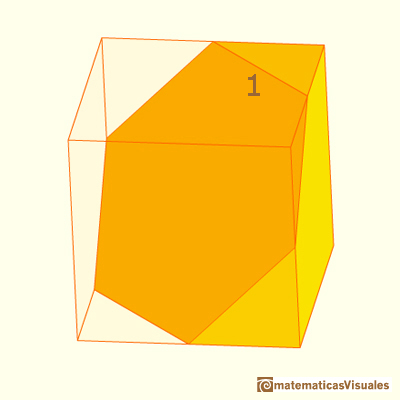
Un volumen muy fácil de calcular de una figura que también tiene la interesante propiedad de teselar el espacio.
5.- Construcciones del octaedro y su volumen
Podemos pensar que el octaedro está formado por dos pirámides de base cuadrada unidas. Su desarrollo es fácil de construir pues sus caras son triángulos equiláteros.
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales dos a dos que contienen las 12 aristas y los 6 vértices del octaedro regular.
Quizás lo primero podría ser recordarnos una manera de coger y mirar el octaedro. El octaedro está formado por 2 pirámides de base cuadrada unidas.
Si, por ejemplo, el lado es 1 entonces la base tiene 1 de área y la altura de las dos pirámides es la diagonal de un cuadrado unitario.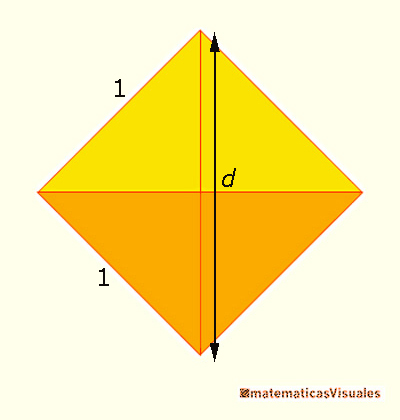
La diagonal de un cuadrado de lado 1 es:
Por lo tanto, el volumen de un octaedro de lado 1 es:
Y el volumen de un octaedro de lado a es:
Usando la fórmula del volumen de la pirámide (que es un tercio del área de la base por la altura) y mirando adecuadamente un octaedro vemos que es muy sencillo calcular su volumen.
Ahora usaremos la misma fórmula para calcular el volumen del tetraedro.
6.- El tetraedro y su volumen
El Tetraedro es el sólido platónico más sencillo. Conocido desde épocas muy remotas.
Es descrito por Luca Pacioli en su libro 'La Divina Proporción' donde podemos ver una ilustración de Leonardo da Vinci.
El tetraedro es una pirámide y su volumen es un tercio del área de la base por la altura. Así podemos calcular su volumen pero vamos a ver una construcción (que ya nos enseñó Kepler) que nos va a facilitar la tarea.
Se puede construir un tetraedro dentro de un cubo: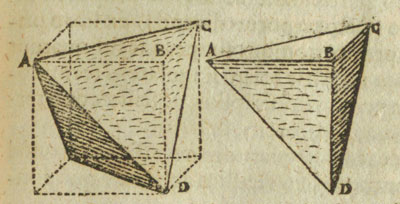
Tomando dos diagonales de dos caras opuestas de un cubo y uniéndolas adecuadamente obtenemos un tetraedro.
Vamos a ver que el volumen de un tetraedro es un tercio del volumen del cubo que lo contiene.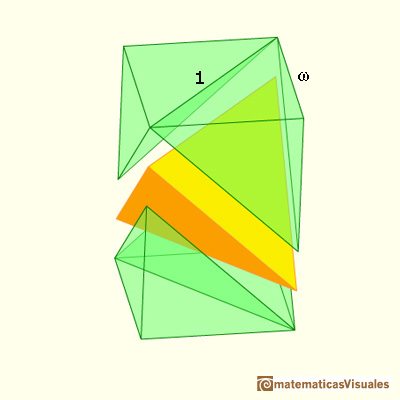
Si la arista del tetraedro es 1 entonces la arista w del cubo es:
El volumen de este cubo lo hemos escrito así:
El cubo está compuesto por el tetraedro amarillo y dos pares de pirámides verdes.
La base de dos pirámides juntas es la base del cubo. Entonces el área de estas dos pirámides (aplicando la fórmula de un tercio del área de la base por la altura) es un tercio del volumen del cubo.
Dos tercios del volumen del cubo está ocupado por las pirámides verdes. Entonces al tetraedro amarillo le queda el tercio restante.
Por lo tanto, el volumen del tetraedro del arista 1 es:
Entonces, el volumen del tetraedro regular de arista a es:
Esta construcción puede generalizarse para cualquier paralelepípedo y obtenemos "tetraedros" no regulares.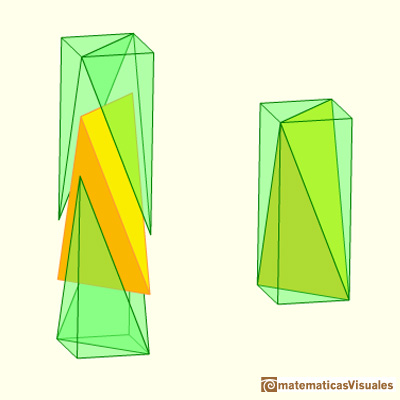
El volumen de estos tetraedros es también un tercio del volumen del paralelepípedo que los contiene.
El volumen del tetraedro parece más dificil de calcular que el del octaedro pero colocándolo adecuadamente en un cubo y aplicando la fórmula del volumen de la pirámide no resulta dificil.
La relación entre el volumen de ambos poliedros es que el volumen del octaedro es cuatro veces el del tetraedro con la misma arista.
Vamos a ver ahora que esta relación se puede obtener sin hacer los cálculos, simplemente razonando con las construcciones de poliedros que hemos hecho.
7.- Relación entre el volumen del octaedro y el del tetraedro
Una manera de construir nuevos poliedros es añadir pirámides a las caras de otro poliedro.
Un ejemplo interesante es partir de un octaedro y añadirle cuatro tetraedros:
Con este dato podemos calcular el volumen del tetraedro. Consideremos un tetraedro de lado 2: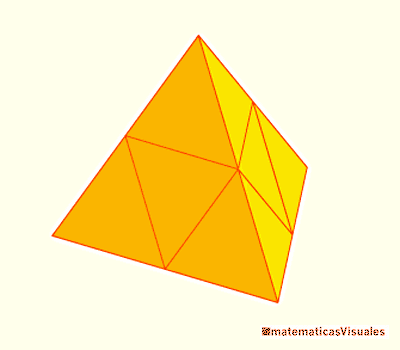
Entonces podemos escribir la relación: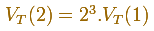
Un tetraedro de arista 2 está formado por un octaedro y 4 tetraedros de arista 1:
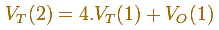
Entonces, el volumen del octaedro es cuatro veces el del tetraedro y volvemos a calcular el volumen del tetraedro
Por lo tanto, el volumen del tetraedro es:
Una vez que tenemos esta relación entre los volúmenes del octaedro y del tetraedro volvemos a fijarnos en el medio cubo con sección hexagonal.
Construiremos un nuevo poliedro, estudiaremos sus propiedades y lo usaremos para calcular el volumen del octaedro.
8.- Un poliedro formado por ocho medios cubos y su volumen
Con ocho de estos medios cubos podemos construir un poliedro que tiene interesantes propiedades.
La primera de las propiedades de este poliedro es que como ya hemos calculado el volumen de medio cubo. entonces el volumen de este poliedro es muy sencillo:
9.- Este poliedro es un sólido arquimediano
Además este poliedro es un sólido arquimediano. Pertenece a la segunda familia de poliedros más famosa. Sus caras son poliedros regulares no todos iguales. En este caso vemos que tiene 6 cuadrados y 8 hexágonos. Todos sus vértices tienen que ser iguales.
Este es el desarrollo plano de esta figura:
10.- Este poliedro tesela el espacio
Por la manera de construir este poliedro a partir de medios cubos vemos que tiene la propiedad de teselar el espacio.
Es decir, que uniendo poliedros de este tipo del mismo tamaño podemos llenar el espacio sin dejar huecos entre ellos. Al igual que el cubo es el único poliedro platónico que tesela el espacio, este poliedro es el único de los arquimedianos con esta propiedad.
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
Escribe Steinhaus: "La posibilidad de llenar totalmente el espacio con poliedros congruentes plantea la interesante cuestión de lograr que solamente haya en cada vértice 4 poliedros congruentes (es imposible tener sólo 3)."
El octaedro truncado es la solución. "No existe ningún otro poliedro que tenga estas propiedades y dé, por consiguiente, la más sencilla descomposición del espacio en partes congruentes". (Steinhaus)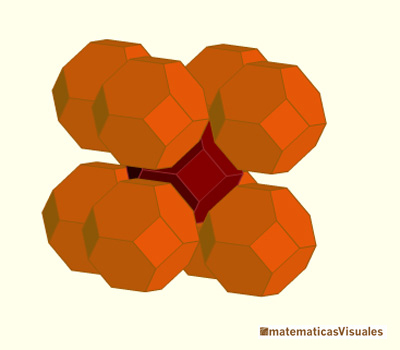
11.- El poliedro se llama octaedro truncado
Es un poliedro arquimediano que podemos ver como un octaedro al que se le han quitado seis pirámides en sus vértices. Por lo tanto, su nombre es octaedro truncado.
12.- Calculando el volumen del octaedro
El volumen del octaedro se puede calcular a partir del octaedro truncado (que ya sabemos que tiene un volumen muy sencillo de calcular).
Por otra parte, sabemos que hay una relación entre el volumen del octaedro de lado 3 y el de lado 1:
El octaedro de lado 3 está formado por un octaedro truncado de lado 1 y 3 pares de pirámides. Cada par forma un octaedro de lado 1.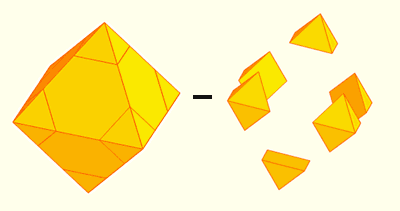
Por lo tanto, podemos escribir:
El volumen del octaedro de lado 1 es:
Si sabemos el volumen del octaedro ya podemos calcular el volumen del tetraedro pues sabemos que es la cuarta parte.
Hemos podido calcular el volumen del octaedro y el del tetraedro sin recurrir a la fórmula del volumen de la pirámide. Manipulando las construcciones de los poliedros y viendo sus propiedades. También hemos usado la relación entre los volúmenes de figuras semejantes.
13.- Construcción de un tetraedro con origami
Para terminar vamos a construir dos figuras usando dos técnicas básicas: origami y cartulina pegada.
Con origami construiremos un tetraedro que podremos poner dentro de una cajita cúbica hecha con cartulina.
Este es el modelo de la caja cúbica que se pueden descargar. El rectángulo es el tamaño de papel que necesitamos para el plegado de un tetraedro que cabe perfectamente en la caja:
Estas son las instrucciones para el plegado del tetraedro con origami modular:
Me gustaría haber podido transmitir gusto por la construcción de poliedros y la idea de que además de la belleza que tienen tambien su manipulación nos permite hacer razonamientos matemáticos de un modo sencillo. Ver y tocar las Matemáticas.
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
SIGUIENTE
Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
ANTERIOR
Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.
MÁS ENLACES
Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.
Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.
Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.
Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
Técnica simple para construir poliedros pegando discos de cartulina.
El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.
Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.
Con tres rectángulos áureos podemos construir un icosaedro.
El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.
Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.
Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.
Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
Desarrollos planos de pirámides truncadas por un plano oblicuo.