|
|
Llenando el espacio con una escultura matemática
Taller de Talento Matemático de Aragón
Día Internacional de las Matemáticas 2023
Para celebrar el Día Internacional de las Matemáticas 2023 el
Taller de Talento Matemático de Aragón
organizó la actividad 'Llenando el espacio con una escultura matemática'.
Se realizó el viernes 10 de marzo de 2023 en la Facultad de Ciencias del Campus San Francisco de la
Universidad de Zaragoza.
Diseño del cartel: Miguel Cardil
Puedes
descargar el cartel aquí.
El año 2024, la construcción que realizamos tiene como base otro poliedro que tesela el espacio, el dodecaedro rómbico.

Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.
En la sesión del año 2023 construimos una escultura matemática multicolor que está expuesta en el vestíbulo de la
Facultad de Ciencias (edificio de Matemáticas) de Zaragoza.
Fue una actividad del Taller de Talento Matemático abierta a todo el mundo.
Puedes ver y divulgar el resumen de la actividad con este
díptico que puedes descargar aquí.
Diseño: Miguel Cardil
Los participantes necesitan tijera, regla y pegamento.
Un pegamento ideal para este tipo de construcciones es el pegamento transparente de tubo, tipo Imedio-UHU.
La escultura matemática está formada por módulos que hicimos con cartulina.
Este es el módulo que hicimos:
Haremos muchos de estos módulos y, entre todos, los uniremos para formar nuestra escultura.
Algo así pero ¡muy grande!
El viernes día 10 de marzo de 2023 hicimos el taller.
Participaron más de cien personas, la mayoría, chicos y chicas de secundaria.
Entre todos hicimos la escultura matemática.
Está expuesta en el vestíbulo del Edificio de Matemáticas de la Facultad de Ciencias de la Universidad
de Zaragoza.
Estas son algunas imágenes de la actividad y del resultado:
El módulo está basado en un poliedro llamado octaedro truncado.
El octaedro truncado es un poliedro de la familia de los poliedros arquimedianos (en honor a Arquímedes).
Algunos poliedros arquimedianos, pero no todos, se obtienen cortando adecuadamente los vértices de algún
poliedro regular o platónicos. A este proceso se le llama 'truncamiento'. Partiendo del octaedro obtenemos
el octaedro truncado.
INVESTIGA
Puedes buscar información sobre estas dos familias de poliedros: los sólidos platónicos y los arquimedianos.

Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
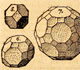
Exposición sobre los sólidos arquimedianos realizados por alumnos de 1ºESO del IES Alonso Quijano de Alcalá de Henares.
El octaedro truncado tiene una propiedad sorprendente que es la que utilizaremos para construir
la escultura.
Aunque no lo parezca a primera vista, es un poliedro
que rellena el espacio sin dejar huecos. Es decir, podemos poner poliedros del mismo tamaño juntos de modo
que no dejen ningún hueco entre sí. Decimos que el octaedro truncado 'tesela' el espacio. Es como un
mosaico pero tridimensional.
El poliedro más sencillo que tesela el espacio es el cubo.
Una escultura como esta la hicimos en una sesión del
Taller de Talento Matemático de Zaragoza
el día 21 de Octubre de 2016.
Ahora la vamos a hacer a lo grande pero el espíritu es el mismo: pasar un rato agradable
haciendo una construcción matemática bonita.
Lo que sigue es una explicación más detallada sobre el octaedro truncado y otros poliedros relacionados como
el octaedro, el cubo y el cuboctaedro.
También se pueden descargar las plantillas que usamos para hacer esta escultura.
Estos son algunos ejemplos de otras sesiones del Taller de Talento Matemático relacionadas con la
construcción de poliedros:

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
La construcción que vamos a hacer en cartulina está inspirada en este detalle que vi en la barandilla de un pantano
(si no estoy equivocado, se trata del pantano del Atazar, en Madrid):
Muy semejante a la que se encontraba en la calle de Francisco Silvela, junto a la Avenidad de América en Madrid
(esta barandilla, con tanto interés matemático, ya no existe y ha sido sustituida por otra muy anodina):

1.- Esqueleto de cuboctaedro y octaedro truncado
Esta es la construcción que vamos a hacer.
Podemos verla como el esqueleto de dos poliedros que vamos a estudiar: en el hueco interior, el cuboctaedro y el
exterior de la figura delimita un octaedro truncado.
Estos dos poliedros pertenecen a la familia de los sólidos arquimedianos (por el famoso matemático griego de
la antigüedad, Arquímedes).
Están emparentados con dos poliedros platónicos, el cubo y el octaedro.
INVESTIGA
Puedes buscar información sobre estas dos familias de poliedros: los sólidos platónicos y los arquimedianos.

2.- El cubo y el octaedro son poliedros duales
INVESTIGA
Ya hemos tratado el concepto de dualidad de poliedros en dos sesiones anteriores del Taller de Talento Matemático.
Puedes obtener algo de información mirando los apartados 2 y 6 de la sesión del curso 2015-16:

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
También en los apartados 3 y 4 del curso 2013-14:

Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.
Ahora nos interesa revisar la dualidad entre dos poliedros sencillos, el cubo y el octaedro.
La idea es contar sus elementos fundamentales: caras, aristas y vértices.
Vamos a contar las caras, aristas y vértices del cubo:
También del octaedro:
Vemos que el cubo y el octaedro tienen el mismo número de aristas e intercambian el número de caras y el de vértices.
Entonces podemos decir que el cubo y el octaedro son poliedros duales.
INVESTIGA
Puedes buscar información sobre la dualidad entre poliedros y encontrar otras parejas de poliedros duales.
Otro asunto muy relacionado es el de la Característica de Euler (o fórmula de Euler de los poliedros). Es un
concepto, en principio, sencillo pero profundo.

3.- El cubo y el octaedro en posición recíproca
Nos interesa ahora fijarnos en el hecho de que el cubo y el octaedro tienen el mismo número de aristas.
Podemos emparejar las aristas de estos poliedros y colocarlas de modo que se corten por la mitad perpendicularmente.
Resulta la siguiente figura y decimos que el cubo y el octaedro están en 'posición recíproca'.
INVESTIGA
Puedes obtener más información de esta figura en la siguiente página:

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

4.- El cuboctaedro
En la combinación entre cubo y octaedro hay una parte común a los dos poliedros, 'dentro' de la figura.
Esta parte común resulta ser un sólido arquimediano que se llama cuboctaedro.
INVESTIGA
Puedes ver más información sobre el cuboctaedro en estas páginas:

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

5.- Truncando el cubo y el octaedro
Si partimos de un octaedro podemos obtener un cuboctaedro 'cortando las esquinas'. Este procedimiento nos permite
hacer nuevos poliedros a partir de otros y lo llamamos 'truncar'.
El cuboctaedro tambien es un truncamiento de un cubo.
Podemos truncar estos poliedros con mayor o menor 'profundidad'. En dos casos obtenemos otros poliedros arquimedianos: el
cubo truncado y el octaedro truncado (y, después de ver el cuboctaedro, ya hemos llegado al segundo poliedro que estamos
estudiando, el octaedro truncado).
La siguiente ilustración nos muestra estas relaciones:
INVESTIGA
Puedes ver más ideas relacionadas con los truncamientos del octaedro y del cubo en la siguiente página:
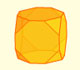
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

6.- El octaedro truncado
Truncando adecuadamente un octaedro obtenemos un sólido arquimediano llamado octaedro truncado.
Por cada cara triangular del octaedro tenemos un hexágono regular. Es decir, el octaedro truncado tiene 8 hexágonos.
Por cada vértice del octaedro tenemos un cuadrado. Entonces, el octaedro truncado tiene 6 cuadrados.
INVESTIGA
En la siguiente página puedes ver más propiedades del octaedro truncado.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

7.- El octaedro truncado tesela el espacio
A veces nos planteamos cómo rellenar el plano con polígonos. Estas configuraciones se llaman mosaicos y cada pieza es una
tesela.
Los casos más sencillos es cuando el mosaico está formado por polígonos iguales y regulares. Entonces podemos decir que
el cuadrado, el triángulo equilátero y el hexágono equilátero 'teselan el plano'.
El problema es mucho más difícil si pensamos en el espacio. La teselación del espacio más simple es la que está formada por
cubos. El cubo es el único sólido platónico que tesela el espacio.
No parece tan inmediato que el octaedro truncado también tesela el espacio.
El octaedro truncado es el único poliedro arquimediano que tesela el espacio.
INVESTIGA
En la siguiente página puedes comprobar intuitivamente, con una aplicación interactiva, que el
octaedro truncado tesela el espacio.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

8.- El octaedro truncado está formado por ocho medios cubos
¿Cómo se podría explicar la propiedad del octaedro truncado de teselar el espacio?
Parece una figura no relacionada con el cubo que, podemos decir, que es el poliedro más regular y simple que tesela el
espacio.
Pero ya sabemos que entre el octaedro y el cubo hay una relación muy estrecha.
Podemos ver el octaedro truncado como una figura que está formada por 8 medios cubos.
INVESTIGA
Para comprender mejor la teselación del octaedro truncado primero puedes ver un modo de cortar un cubo por la mitad que
resulta muy interesante:
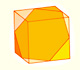
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
Uniendo 8 de esos medios cubos obtenemos un octaedro truncado:

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

9.- Construcción del esqueleto de cuboctaedro y octaedro truncado
Las siguientes plantillas se pueden descargar y construir el esqueleto del cuboctaedro y del octaedro truncado:
Para construir la escultura matemática uniremos las figuras usando este tipo de piezas:
Recortamos y doblamos las piezas (8 piezas de 4 colores):
Pegamos las piezas:
Las pegamos teniendo cuidado en emparejar bien los colores para formar la figura:
Con la siguiente plantilla puedes construir unas piezas que nos servirán como pirámides:
Las podemos poner hacia dentro. Así el cuboctaedro interior con las pirámides forma un
octaedro. Podemos decir que el cuboctaedro es un truncamiento del octaedro.
Las podemos poner hacia afuera. Entonces el octaedro truncado con las pirámides forma un
octaedro.
Las siguientes dos plantillas tienen dibujos de polígonos con solapas. Cuadrados, triángulos y hexágonos.
Con ellas podemos construir cuboctaedros, octaedros truncados o cerrar algunas caras de nuestro 'esqueleto':

10.- Variante de la construcción
La siguiente plantilla tiene las piezas para una variante de la construcción:
Recortamos y doblamos las piezas:
Pegamos las piezas por separado:
Pegamos las 8 piezas para formar la figura:

11.- Teselando el espacio
Construyendo muchas figuras podemos hacer una teselación de (una parte) del espacio con
octaedros truncados
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE SIGUIENTE

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
 ANTERIOR ANTERIOR

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión del TTM (Zaragoza, 8 de marzo de 2024). Con plantillas para descargar y construir dodecaedros rómbicos y celdas de abejas.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
|
























































































 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR


















