Truncar un poliedro significa cortar sus vértices (o sus aristas). En esta página cortaremos los vértices de algunos poliedros para obtener otros.
Si partimos de los sólidos platónicos (poliedros regulares) y truncamos los vértices de un modo simétrico obtenemos algunos
de los sólidos arquimedianos (poliedros semirregulares).
Ya hemos estudiado el tetraedro truncado que es el único poliedro arquimediando que se obtiene al truncar el tetraedro.
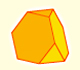
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
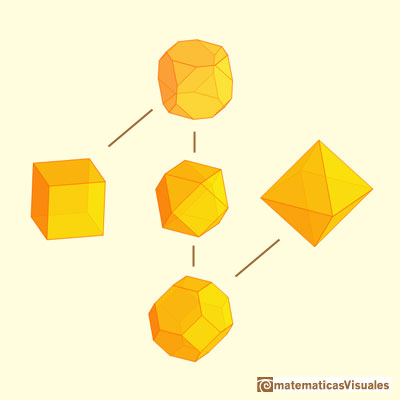
Vamos a investigar truncamientos del cubo y del octaedro. Ambos poliedros están relacionados pues son poliedros duales.
Empezamos con el cubo y cortamos los vértices de modo que obtenemos triángulos equiláteros. Las caras cuadradas del cubo son ahora octógonos (en principio, irregulares)
Podemos truncar los ocho vértices de modo que las caras cuadradas orignales sean octógonos regulares. El resultado se llama cubo truncado.
El cubo truncado (o hexahedro truncado) es un sólido arquimediando. Tiene 14 caras regulares (6 octógonos y 8 triángulos).
Podemos construir un cubo truncado con mucha facilidad usando cartulina y gomas elásticas:
Cubo truncado que es una lámpara en el Palau Baró de Quadras, edificio modernista en Barcelona
Si truncamos el cubo con mayor profundidad obtenemos otro sólido arquimediano, el cuboctaedro. Tiene 6 cuadrados y 8 triángulos equiláteros.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
También podemos obtener un cuboctaedro truncando un octaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
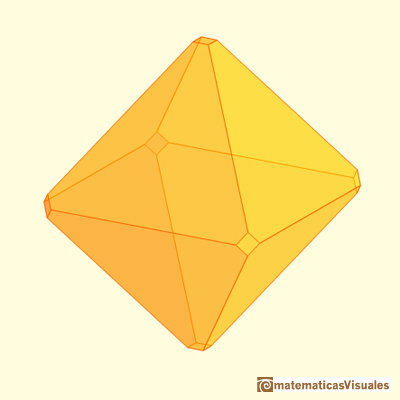
Otro truncamiento del octaedro tiene el nombre de octaedro truncado. Obtenemos este poliedro cuando truncamos los vértices de un octaedro de modo que sus
caras triángulares se transforman en hexágonos regulares.
Puesto que cuatro caras se unen en los vértices de un octaedro, cuando truncamos esos vértices obtenemos cuadrados. El octaedro truncado tiene 6 cuadrados y 8 hexágonos.
También es unos de los poliedros arquimedianos.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
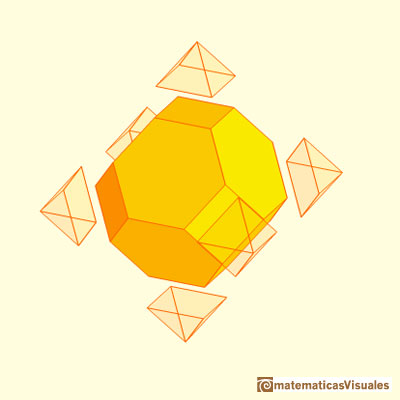
Obtenemos un cuboctaedro truncando un cubo o un octaedro. Podemos ver esta relación como una consecuencia de la dualidad entre el cubo y el octaedro.
Así vio Kepler esta relación:
El cubo y el octaedro, al ser poliedros duales, tienen el mismo número de aristas.
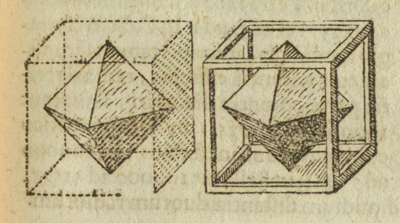
Si pensamos en la figura formada por un cubo y un octaedro puestos de modo que sus aristas se bisecan ortogonalmente
obtenemos una figura que es un compuesto de cubo y octaedro. A veces se dice que están en posición recíproca.
La parte común de este compuesto es un cuboctaedro. De hecho la figura compuesta es la primera estelación del cuboctaedro.
Los vértices de este cuboctaedro están en los puntos medios de los lados.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.
Si nos fijamos en los vértices de esta figura compuesta, el cuboctaedro estrellado, resulta que son los vértices de un poliedro llamado
dodecaedro rómbico. Un poliedro con interesantes propiedades que es el dual del cuboctaedro. En los siguientes meses dedicaremos atención a este poliedro.
REFERENCIAS
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
MÁS ENLACES

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.





















 SIGUIENTE
SIGUIENTE



























 ANTERIOR
ANTERIOR

