El papel que usamos normalmente tiene un tamaño estándar. En muchos países del mundo (pero no en Estados Unidos, Canadá o Méjico)
la estandarización del tamaño del papel se basa en ISO 216 y llamamos a estos tamaños DIN A0, DIN A1, DIN A2, DIN A3, DIN A4, etc.
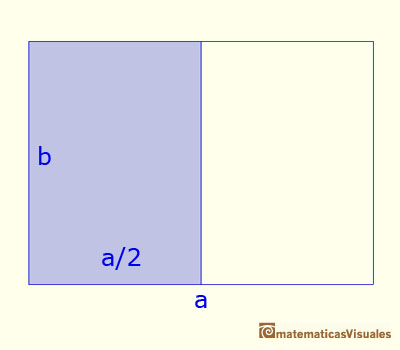
La base del estándar, DIN A0 se define como el rectángulo de un metro cuadrado de superficie. Sucesivos tamaños de papel en la
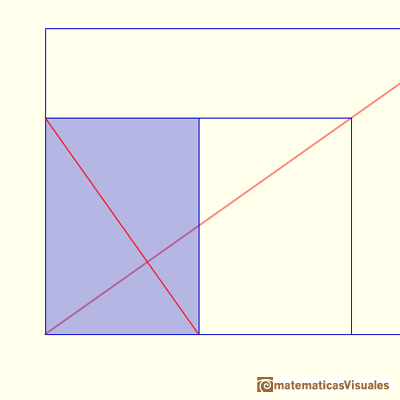
serie A1, A2, A2, A4, etc., se definen dividiendo por la mitad el tamaño anterior por el largo. El objetivo es que estas mitades
tengan otra vez la misma proporción. Es decir, todos estos rectángulos son semejantes.
Vamos a calcular esta proporción, es decir, el cociente entre el largo y al ancho:
Puesto que los rectángulos son semejantes, esta proporción verifica:
Por lo tanto:
O también:
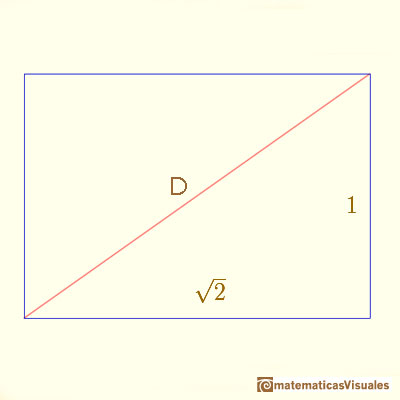
El lado largo es igual a la diagonal del cuadrado cuyo lado es el lado corto del rectángulo:
El tamaño DIN A0 tiene un metro cuadrado. Podemos calcular sus dimensiones (redondeadas a los milímetros))
En una fotocopiadora, cuando queremos reducir de A3 a A4 se nos muestra una proporción del 71%. ¿Por qué?
Vamos a estudiar algunas características de este rectángulo.
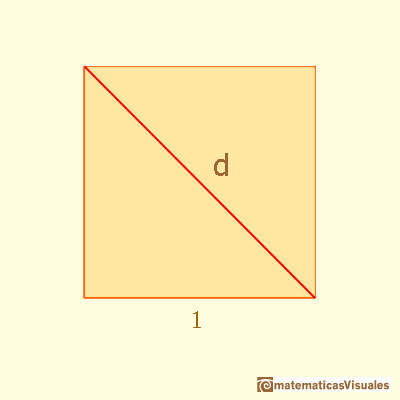
Recordamos que la diagonal de un cuadrado de lado 1 es:
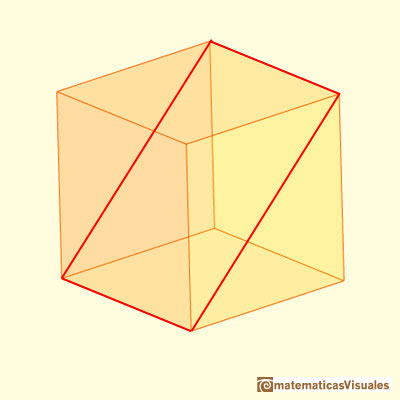
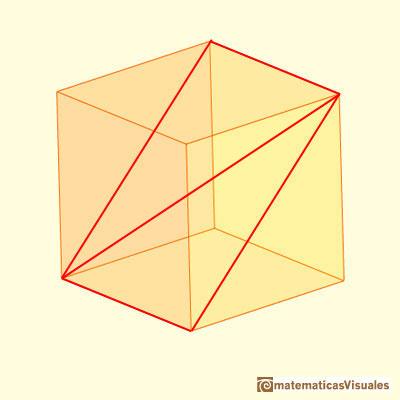
Encontramos nuestro rectángulo como una sección de un cubo:
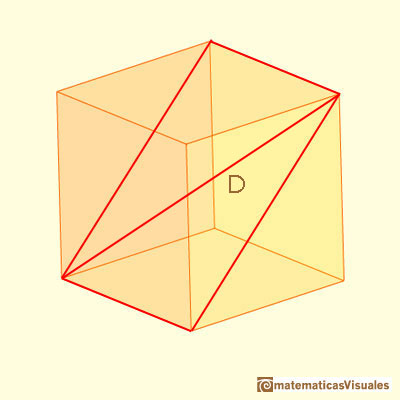
Una diagonal del rectángulo:
Podemos calcular D como una aplicación básica del teorema de Pitágoras:
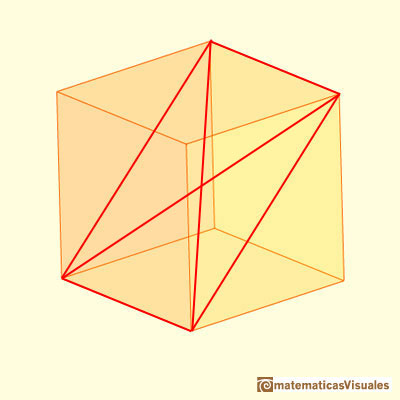
Si consideramos las dos diagonales de esta sección, el punto de intersección es el centro del cubo:
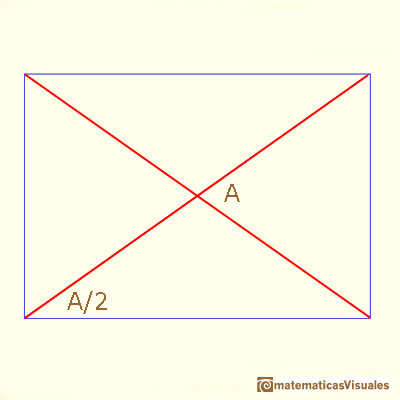
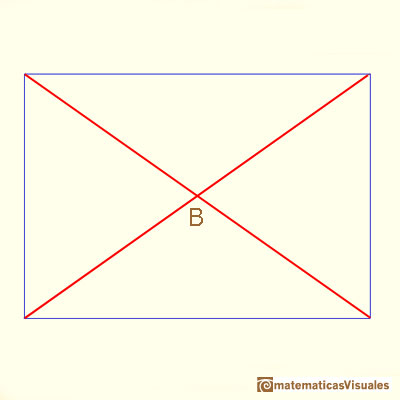
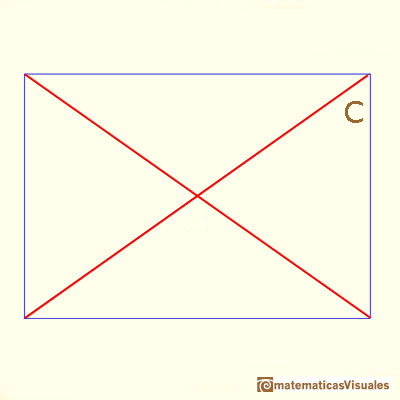
Ahora vamos a estudiar los ángulos entre las dos diagonales (para esto necesitaremos unos conocimientos básicos de trigonometría):
El ángulo C se calcula fácilmente:
También:
Nos volveremos a encontrar con estos ángulos cuando estudiemos el cubo achaflanado y el dodecaedro rómbico porque nuestro rectángulo está
relacionado con estos poliedros.

Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
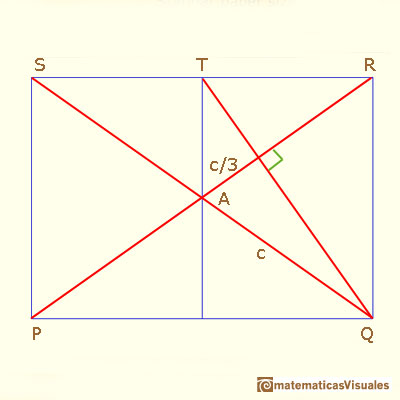
Una visión geométrica de las propiedades de este rectángulo nos facilita otro modo de calcular el ángulo A:
¿Cómo lo podemos explicar?
Primero, los segmemtos PR y QT son perpendiculares porque si rotamos 90 grados en sentido contrario a las agujas del reloj el rectángulo ....
Segundo, las rectas PR y QT son dos medianas del triángulo QRS, entonces el baricentro divide ...
Ahora podemos escribir cos A ...
MÁS ENLACES

Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
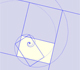
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

Algunas series geométricas se pueden sumar fácilmente. Podemos ver un ejemplo muy intuitivo cuando la razón es 1/4

Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.

Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.

La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.

Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?

Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.

A partir de un rombicuboctaedro podemos añadir pirámides a sus caras. Obtenemos un precioso poliedro que parece una estrella.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.

Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices






 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR































