Ya hemos estudiado la proporción áurea y varias propiedades del rectángulo áureo.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

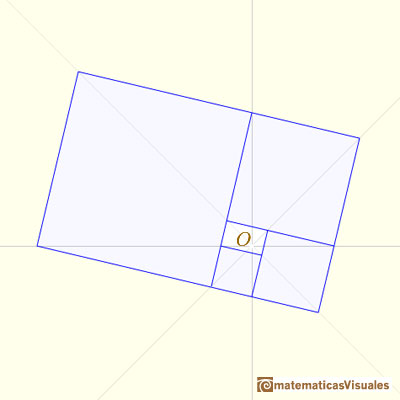
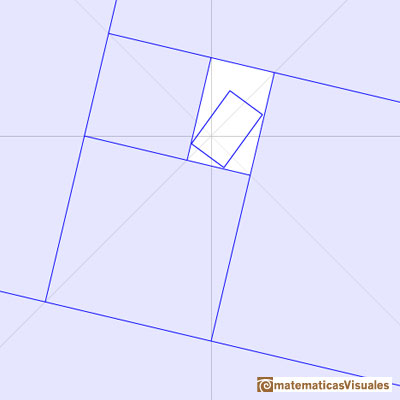
Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
Cuando dividimos un rectángulo áureo en un cuadrado y otro rectángulo este nuevo rectángulo es semejante
al inicial y es, también, un rectángulo áureo. Podemos repetir este proceso indefinidamente y obtendremos una sucesión de rectángulos.
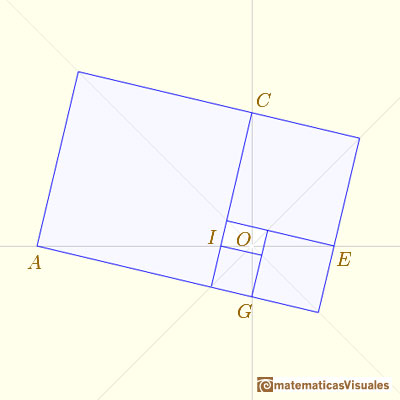
Existe un punto especial que llamamamos O
Para obtener el siguiente rectángulo a partir de uno inicial podemos considerar la transformación que es un producto (composición) de
una dilatación de centro O
y una rotación (un cuarto de vuelta en sentido horario o negativo en torno a O)
Esta transformación es una rotación dilatativa.
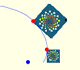
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.
En el siguiente applet podemos ver una rotación dilatativa continua:
Ahora vamos a calcular las coordenadas polares de varios puntos.
El polo es O
Tomando OE como la recta origen y la distancia OE como unidad de medida, de modo que E es
Desde E hasta C la rotación dilatativa en torno a O tiene razón de dilatación
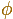 y es un giro de un cuarto de vuelta en el sentido positivo.
y es un giro de un cuarto de vuelta en el sentido positivo.
En general, podemos calcular una sucesión de puntos
MÁS ENLACES

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
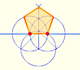
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.

Con tres rectángulos áureos podemos construir un icosaedro.
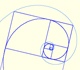
Dos espirales equiangulares contienen los vértices de rectángulos áureos.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
Se puede ver como una rotación dilatativa.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.

En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
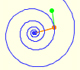
Cualquier dilatación de una espiral equiangular tiene el mismo efecto que una rotación.


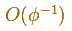
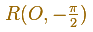
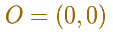
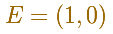
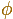 y es un giro de un cuarto de vuelta en el sentido positivo.
y es un giro de un cuarto de vuelta en el sentido positivo.
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR































