Espiral equiangular
"Con respecto a los problemas en los que interviene un origen (o 'polo') fijo O, se suele encontrar que es conveniente determinar un punto P por medio de sus coordenadas polares
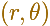
donde 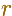 es la distancia
OP y
es la distancia
OP y
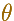 es el ángulo que la dirección
OP hace con una recta inicial dada, OX, que se puede identificar con el eje x de las coordenadas cartesianas rectangulares.
Por supuesto, el punto
es el ángulo que la dirección
OP hace con una recta inicial dada, OX, que se puede identificar con el eje x de las coordenadas cartesianas rectangulares.
Por supuesto, el punto 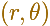 es igual a
es igual a
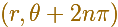 para todo entero n
"
(Coxeter, p.141)
para todo entero n
"
(Coxeter, p.141)
Usamos las coordenadas polares para describir muchas curvas. Por ejemplo, las espirales. Son convenientes para describir isometrías y semejanzas que tienen un punto invariante. Las podemos usar en trigonometría para definir el seno y el coseno de árgulos obtusos y mayores. Las coordenadas polares también están relacionadas con los números complejos.
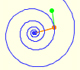
Coxeter introduce la espiral equiangular (o espiral logarítmica) como resultado de una rotación delatativa continua (Coxeter, p. 155).
La ecuación polar de una espiral equiangular es:
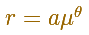
Recibe el nombre de equiangular porque el ángulo entre el radio vector y la recta tangente en cualquier punto de la espiral es constante.
Si 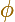 es el ángulo entre el vector posición
OP y la tangente en P entonces (en general, en coordenadas polares)
es el ángulo entre el vector posición
OP y la tangente en P entonces (en general, en coordenadas polares)
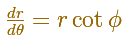
En el caso de la espiral equiangular, podemos escribir
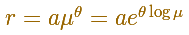
Calculando la derivada
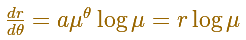
Por lo tanto, la cotangente del ángulo es una constante.
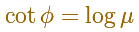
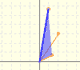
Es decir que el ángulo entre el vector posición OP y la tangente en P es una constante y podemos escribir la ecuación de la espiral equiangular así:
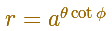
Jacobo Bernouilli la llamó "spiral mirabilis".
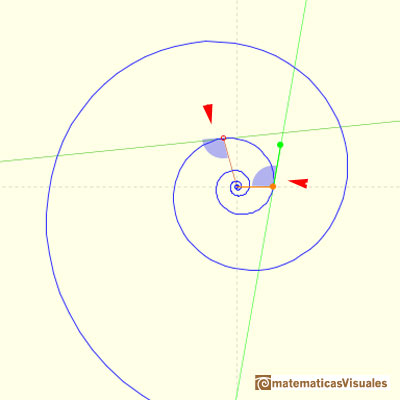
Podemos ver que el ángulo formado por el radio vector y la tangente es constante.
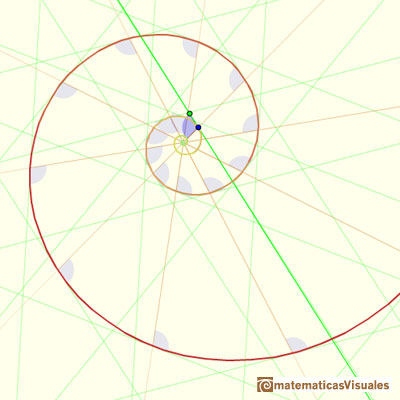
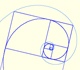
En el siguiente applet podemos jugar con un caso particular: la espiral equiangular áurea. Esta espiral está relacionada con el rectángulo áureo.
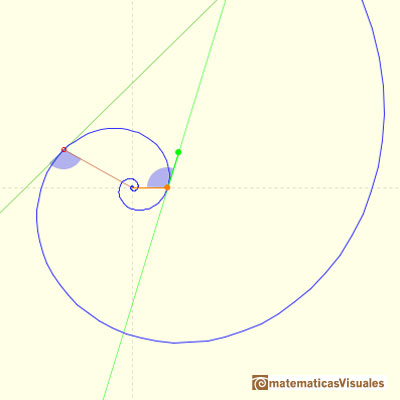
En esta imagen podemos ver una espiral equiangular áurea.
REFERENCIAS
Coxeter - Fundamentos de Geometría. Ed. Limusa(pag. 141 y 155).
Steinhaus - Instantáneas matemáticas. Ed. Salvat (pag. 132).
D'Arcy Thompson - Sobre el crecimiento y la forma. Ed. Cambridge.
 ANTERIOR
ANTERIOR
MÁS ENLACES

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
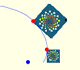
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.













 SIGUIENTE
SIGUIENTE