Ya hemos estudiado la definición y varias propiedades de las espirales equiangulares (o espirales logarítmicas).
En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
Cualquier dilatación de una espiral equiangular tiene el mismo efecto que una rotación.
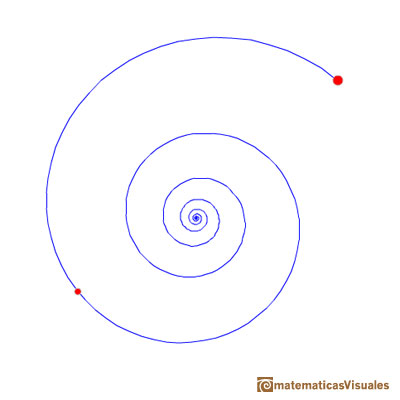
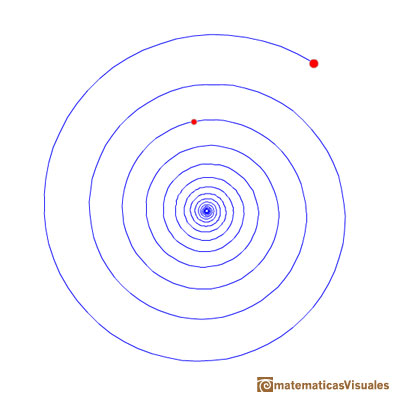
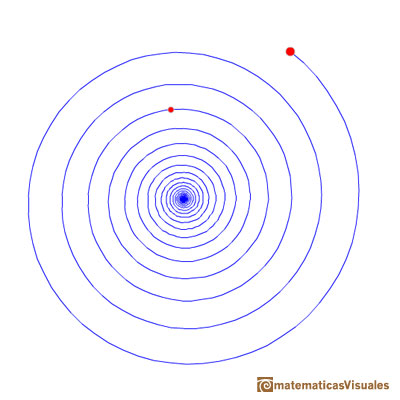
En esta página vamos a ver que hay infinitas espirales equiangulares que pasan por dos puntos dados.
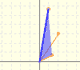
Algunas giran en el sentido contrario a las agujas del reloj (solemos considerar este sentido de giro positivo):
Otras lo hacen en el sentido de las agujas del reloj (que solemos considerar negativo):
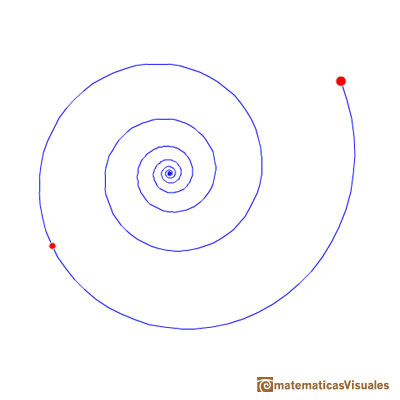
Además, la espiral puede dar varias vueltas desde el inicio hasta alcanzar el otro punto. En el siguiente applet se puede modificar las
vueltas que da la espiral.
REFERENCIAS
Coxeter - Fundamentos de Geometría. Ed. Limusa.
Steinhaus - Instantáneas matemáticas. Ed. Salvat.
D'Arcy Thompson - On Growth and Form. (Cambridge University Press)
MÁS ENLACES
En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
Dos espirales equiangulares contienen los vértices de rectángulos áureos.
La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
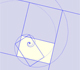
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
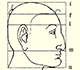
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
Se puede ver como una rotación dilatativa.
SIGUIENTE
ANTERIOR