El origen de los números complejos está relacionado con la solución de la ecuación cúbica (Cardano, en 1545, Bombelli, en 1572). No tiene relación con la solución de la ecuación cuadrática, aunque, a veces, se diga eso. [Para una introducción histórica muy interesante podemos ver el libro de Tristan Needham (págs. 1-5) que nos refiere a Stillwell].
Los números complejos incluyen a los números reales y a números "imaginarios" como la raíz cuadrada de -1.
Si aceptamos los números complejos entonces todas las ecuaciones polinómicas con coeficientes reales (o complejos) tienen raíces o soluciones reales o complejas. (Teorema fundamental del Álgebra, demostrado por Gauss).
En particular
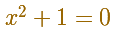
Este es el símbolo que usamos para la unidad imaginaria, la raíz cuadrada de -1. Debemos este símbolo a Euler:
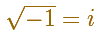
Entonces
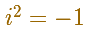
"Los números imaginarios fueron introducidos en los cálculos aritméticos sin la aprobación, e incluso contra los deseos de algunos matemáticos, y sólamente consiguieron una amplia circulación gradualmente y en la medida en que demostraron su utilidad." (Klein, 56)
Sin embargo, años después, "su descubrimiento tuvo al final un impacto profundo en todas las matemáticas, unificando mucho de lo que previamente parecía sin relación y explicando muchas cosas que parecían inexplicables". (Needham, 1)
Una idea importante es la extensión del concepto de número: "Comenzando con los números naturales como el 1 y el 2, continuamos con los enteros, después los números racionales, luego los reales, luego los números complejos (y si tuvieramos tiempo podríamos continuar con los números hipercomplejos). Cada paso está motivado por nuestro deseo de ser capaces de resolver cierto tipo de ecuaciones." (Coxeter, 135)
Después de más de doscientos años, "el siglo diecinueve nos proporcionó al final una comprensión clara de la naturaleza de los números complejos. En primer lugar, tenemos que destacar aquí la interpretación geométrica a la que llegaron varios investigadores al final del siglo. Sería suficiente si mencionáramos a la persona que profundizó más en su esencia y que ejerció la influencia más duradera entre el público, es decir, Gauss." (Klein, 56)
Es bastante usual empezar el estudio de los números complejos fundamentándolos de un modo puramente formal. Así, tanto la definición como las operaciones de suma, resta, multiplicación y división se hacen depender de los números reales.
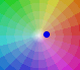
"Además de este tratamiento puramente formal, nos gustaría tener una interpretación geométrica o visual de los números complejos y las operaciones que hacemos con ellos, en la que pudiéramos ver una fundamentación gráfica de consistencia. Esta nos la proporciona la interpretación geométrica habitual en la que la totalidad de los puntos (x,y) del plano en un sistema de coordenadas representa la totalidad de los números complejos z = x+iy." (Klein, 57)
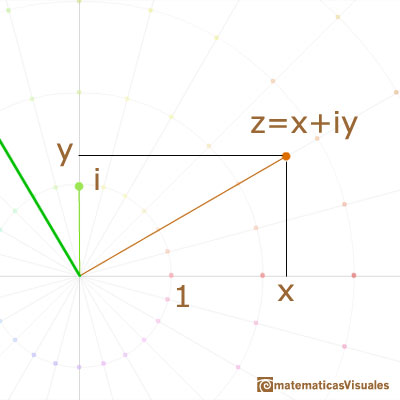
A esta representación la llamamos diagrama de Argand o Plano complejo. Fue formulada por C. Wessel (1797), redescubierta por J.R.Argand (1806), y vuelta a descubrir por Gauss.
Puesto que los números reales ocupan toda la recta real, el eje x, es bastante natural extender la representación de los números complejos como puntos en el plano, como vectores desde el origen o como pares ordenados de números reales.
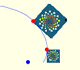
La suma de dos números complejos sigue la regla del paralelogramo y se representa como una traslación del plano en si mismo. Los puntos se suman como vectores desde el origen.
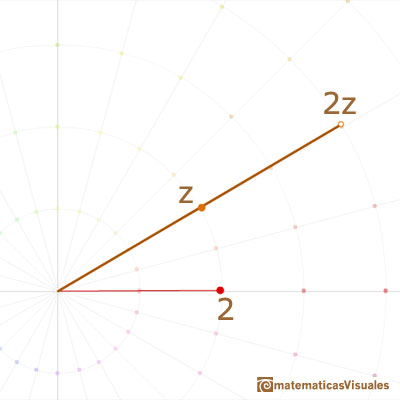
La multiplicación por un número real se nos muestra como una dilatación (incluyendo las contracciones).
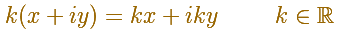
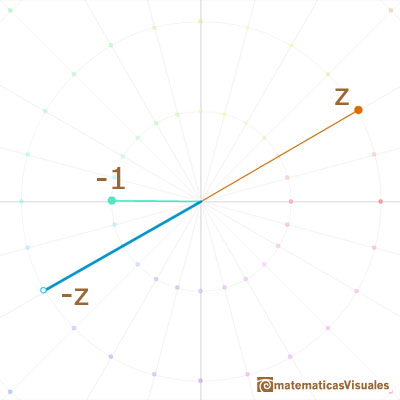
En particular, la multiplicación por -1 es una media vuelta en torno al origen.
Entonces, ¿qué puede ser la multiplicación por la "raíz cuadrada de -1"?. Tiene que ser una transformación cuyo "cuadrado" sea una media vuelta en torno al origen. La respuesta obvia es un cuarto de vuelta en torno al origen. Una rotación de un ángulo recto en el sentido positivo (contrario a las agujas del reloj).
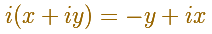
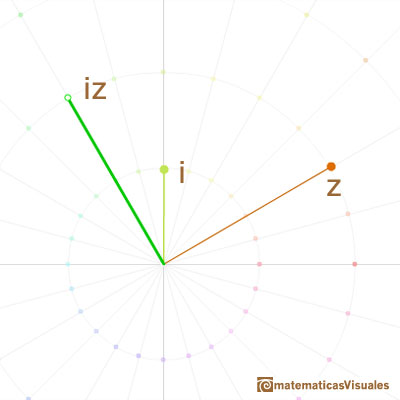
Siguiendo las reglas del Álgebra podemos obtener una fórmula para la múltiplicación de dos números complejos:
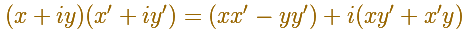
Pero, ¿cuál es el significado geométrico de la multiplicación de dos números complejos?
Multiplicar por un número complejo arbitrario tiene que ser una tranformación que deje el 0, el origen, invariante y que tiene que incluir dilataciones y rotaciones como casos especiales. La transformación obvia de este tipo es una rotación dilatativa. De acuerdo con esto, la operación de multiplicar un punto genérico (x, y) por un punto en particular (a, b) se define como la rotación dilatativa (con centro 0) que transforma (1,0) en (a, b).
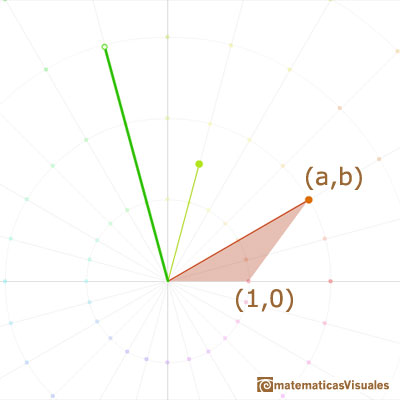
La multiplicación de complejos es una similaridad, una transformación con giro y dilatación (el origen permanece fijo).
Rotación ...
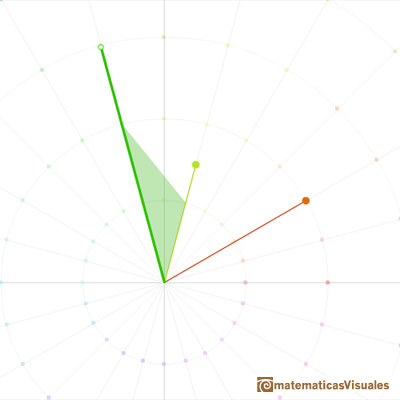
y dilatación.

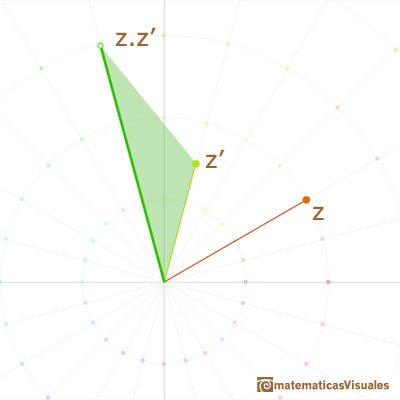
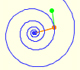
Para comprender la multiplicación de números complejos es mejor usar coordenadas polares. Las coordenadas polares de un número complejo vienen dadas por su distancia al origen (su longitud o módulo) y el ángulo respecto al eje x (que llamamos argumento).
Podemos obtener el resultado de multiplicar dos números complejos sumando sus ángulos (argumentos) y multiplicando sus longitudes (módulos).
En la siguiente representación queremos mostrar la multiplicación de dos números complejos cono una rotación dilatativa continua usando una animación.
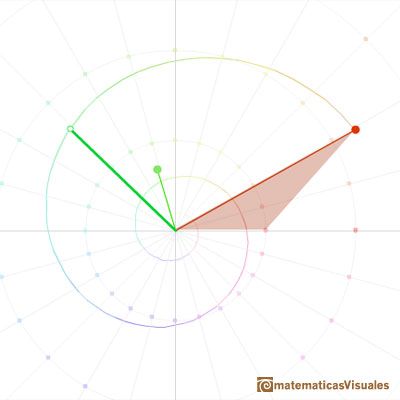
Félix Klein insiste en la importancia de la interpretación geométrica:
"Debo llamar su atención que Gauss establece con total énfasis esta fundamentación de los números complejos por medio de su interpretación geométrica puesto que fue él el primero que destacó la importancia de los números complejos. (...) Para él el derecho de operar con números complejos está justificado por la interpretación geométrica. Así él no adopta de ningún modo el punto de vista formal." ("I must call to your attention the place in Gauss in which this foundation of complex numbers, by means of their geometric interpretation, is set out with full emphasis, since it was this which first exhibited the general importance of complex numbers. (...) For him, the right to operate with complex numbers is justified by the geometric interpretation which one gives to them and to the operations with them. Thus he takes by no means the formal standpoint". ) (Klein, 58)
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES