El volumen del dodecaedro
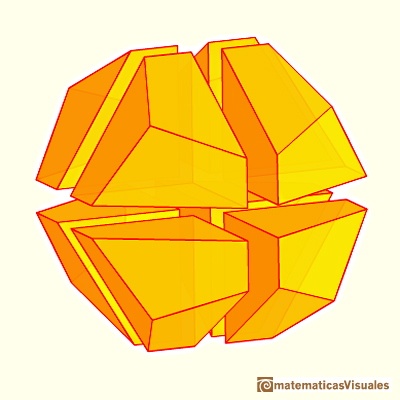
Un octavo de un dodecaedro de lado 2 tiene el mismo volumen que un dodecaedro de lado 1.
Vamos a calcular el volumen de un dodecaedro regular considerando esta figura:
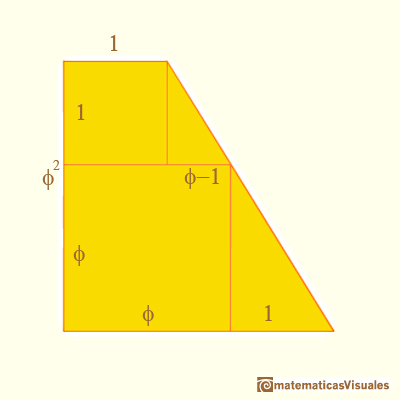
Podemos descomponer un octavo de un dodecaedro de lado 2 en varias piezas para calcular el volumen de estas piezas por separado.
Hay un cubo, tres cuñas y tres pirámides:
Algunas medidas importantes de estas figuras están relacionadas con la proporción áurea:
Recordamos que
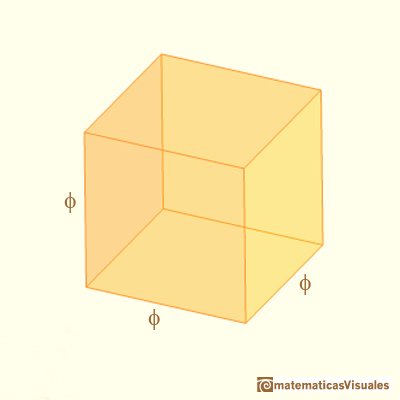
Hay un cubo y su volumen es:
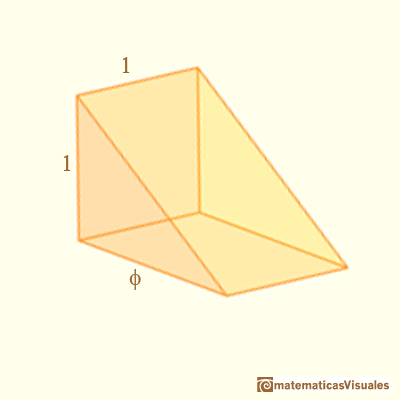
Hay tres cuñas y el volumen de cada cuña es:
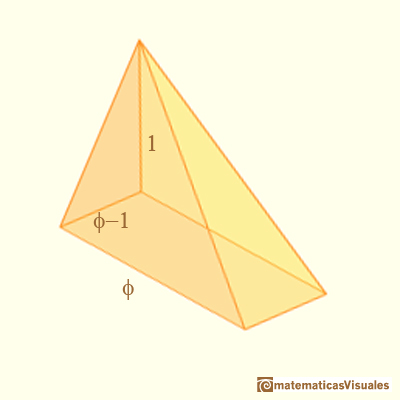
Hay tres pirámides y el volumen de cada pirámide es:
Entonces el volumen de un dodecaedro de lado 1 es:
En general, el volumen de un dodecaedro regular de lado a es:
Algunos minerales, como la pirita, pueden cristalizar en forma de dodecaedro (no regular y que, a veces, llamamos piritoedro):
SIGUIENTE
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
ANTERIOR
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
MÁS ENLACES
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.
Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
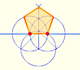
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
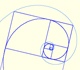
Dos espirales equiangulares contienen los vértices de rectángulos áureos.
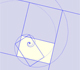
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.