La primera vez que leí sobre la construcción de un pentágono no regular por Durero fue en el libro de Dan Pedoe 'La geometría en el arte', traducido y publicado por Gustavo Gili en 1979.
Pedoe señala que 'el interés de Durero en la construcción de polígonos regulares es un reflejo de su uso durante la Edad Media en la decoración Islámica y Gótica y, desde la invención de las armas de fuego, en la construcción de fortificaciones'.
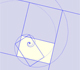
En el libro de Durero 'Underweysung der Messung' ('Los cuatro libros de la medida', publicado en 1525) el autor nos muestra una una construcción exacta del pentágono regular (tomada de Tolomeo) pero aquí estamos jugando con otra construcción del pentágono, en este caso es un pentágono equilátero pero no equiángulo.
Durero pensaba que 'la geometría es la correcta fundamentación de toda la pintura' y quería ser accesible a pintores, artistas en general y artesanos. Escribió sus libros en alemán y su principal interés era práctico y aplicado. La construcción que vamos a estudiar ahora es un buen ejemplo pues aunque es una construcción aproximada es bastante precisa y simple de dibujar.
Para dibujarla usa un 'compás oxidado', es decir, con apertura fija. Esto hace el dibujo mucho más sencillo. [Abu'l-Wafa Al-Buzjani (940-998) fue un matemático y astrónomo que también estuvo interesado en este tipo de construcciones geométricas usando un compás fijo y escribió 'Un libro con aquellas construcciones que son necesarias para el artesano'].

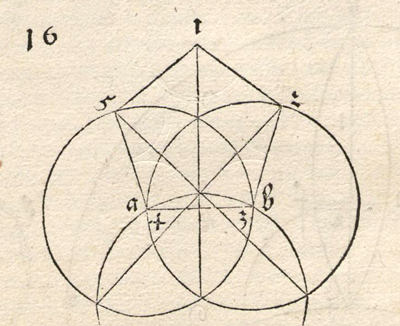
Sabemos que cada uno de los cinco ángulos de un pentágono regular mide 108º. Pedoe escribió que en la construcción aproximada de Durero los ángulos de la base eran de 108º21'58'', además hay dos ángulos menores que 108º y que el ángulo en el vértice superior era mayor que 109º. Estas diferencias no son fácilmente detectables en un dibujo.
Vamos a usar trigonometría para calcular estos ángulos. Por simplicidad, podemos considerar que la longitud del lado es 1.
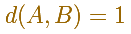
Podemos empezar con el ángulo ABF:
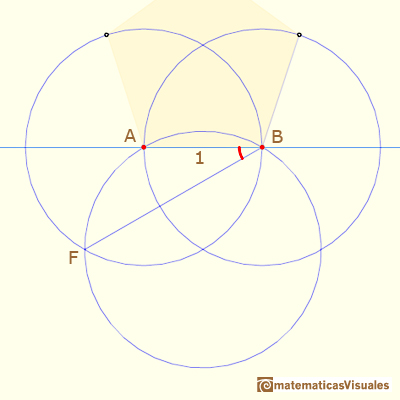
La distancia entre B y F es el doble de la altura de un triángulo equilátero:
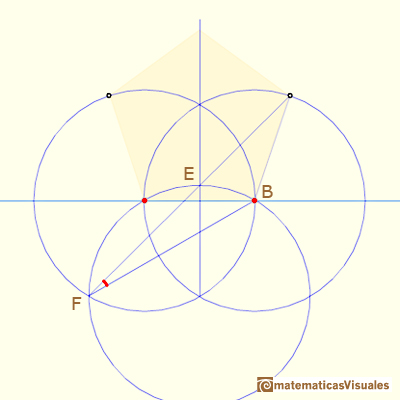
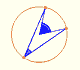
Si recordamos las propiedades de los ángulos centrales e inscritos en una circunferencia, esto es sencillo:
Usando la Ley de los Senos podemos calcular el ángulo FHB:
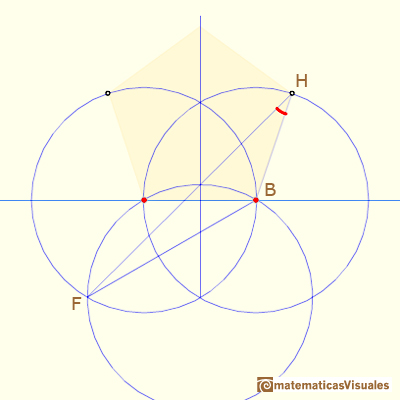
Ahora podemos calcular la medida del ángulo ABH:
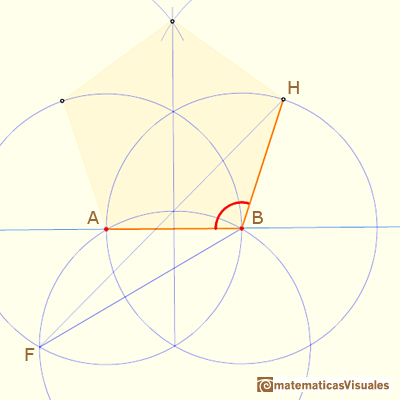
Este ángulo es mayor que 108º, pero el error es muy pequeño.
Para calcular los ángulos HKI y BHK podemos empezar calculando BZ:
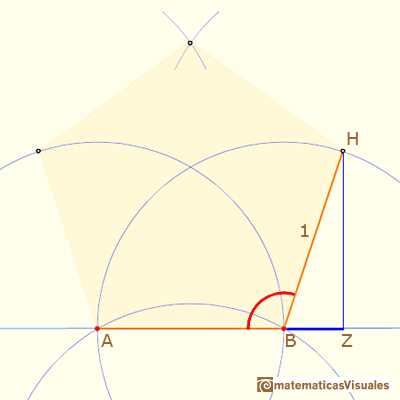
Si M es el punto medio entre H e I:
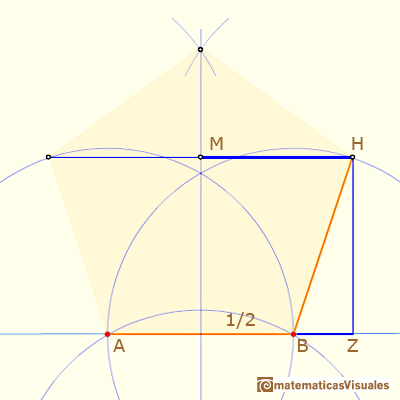
Podemos calcular el ángulo MHK:
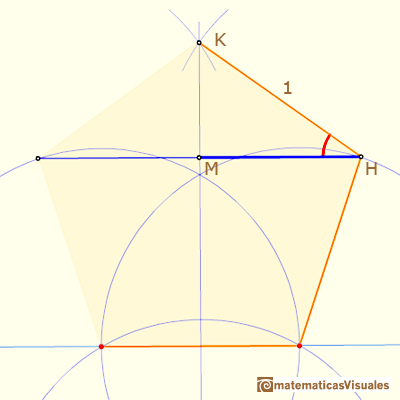
Entonces, el triángulo IHK es un triángulo isósceles y es sencillo calcular el ángulo HKI:
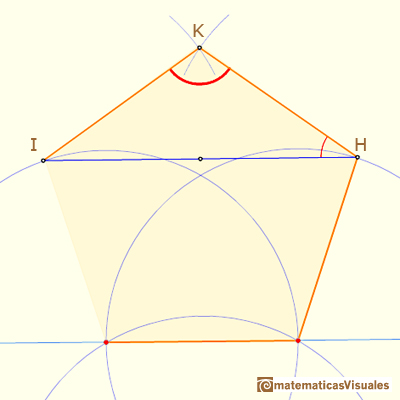
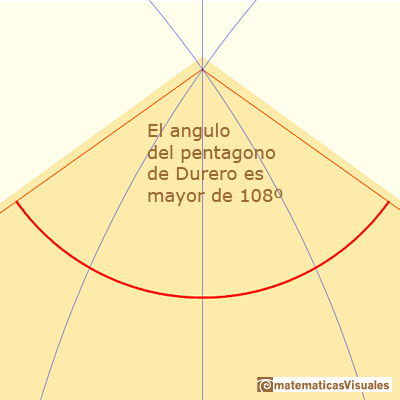
Este ángulo es mayor que 108º.
Terminar esta tarea es sencillo. Recordamos que los cinco ángulos de un pentágono convexo miden tres veces 180º. Podemos deducir la medida del ángulo BHK:
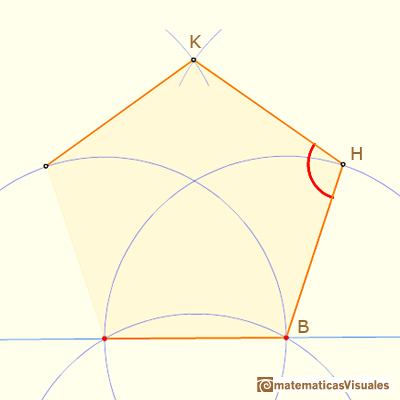
El ángulo en el vértice superior es menor que 108º.
En el siguiente mathlet podemos jugar con el zoom y ver que la aproximación de Durero es muy precisa:
Vemos que la aproximación es excelente.
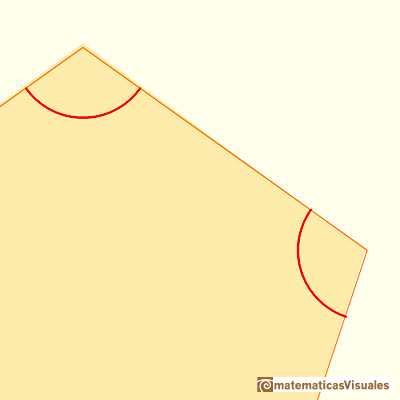
Acercándonos mucho con la lupa vemos el error en los ángulos :

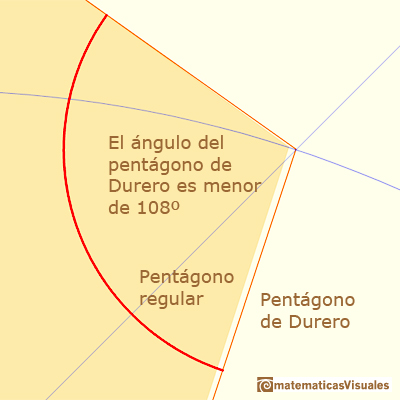
La altura del pentágono de Durero es menor que la altura de un pentágono regular y el ángulo en el vértice superior es mayor:
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES