Alberto Durero (1471-1528) fue un pintor y grabador.
En 1525 publicó el primer libro de Matemáticas en alemán, los "Cuatro libros de la Medida" o "Curso en el Arte de la Medida con regla y compás".
(Underweysung der Messung mit dem Zirckel und Richtscheyt).
Entre otras muchas cosas, nos presenta la primera discusión en alemán sobre las secciones cónicas.

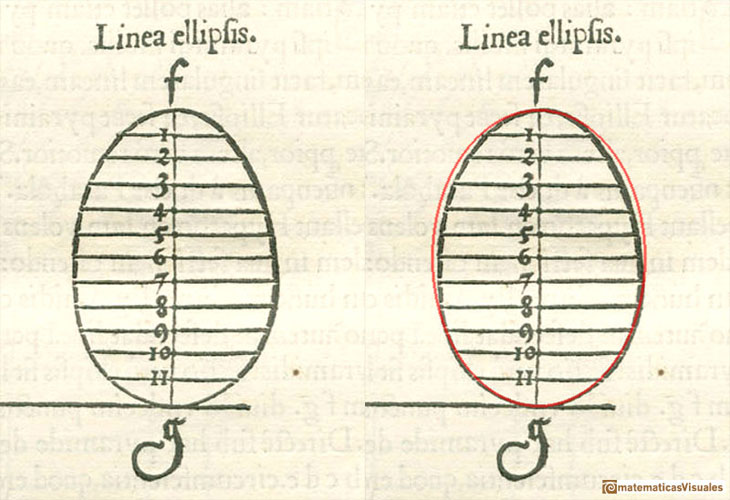
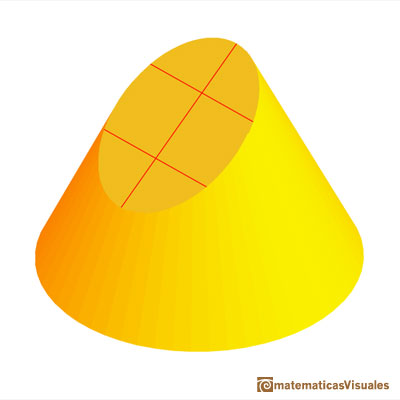
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
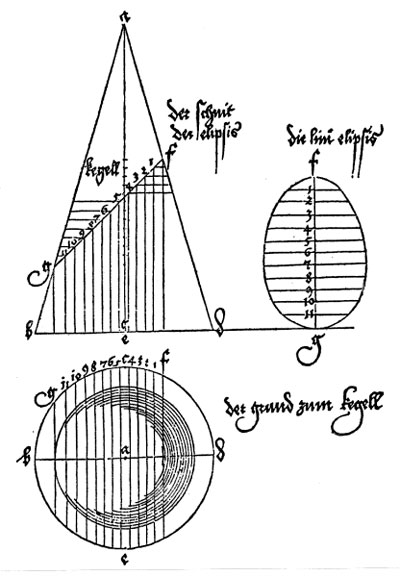
Su método es original y usa vistas en planta y alzado del cono cortado por un plano oblicuo.
Dejándose llevar por la intuición dibujó la curva con forma de huevo, más estrecha por arriba que por abajo. Sabemos que las elipses tienen dos ejes de
simetría y no tienen forma de huevo. Este pequeño error da un poco de pena pues su método es excelente.
El error se puede subsanar usando Matemáticas elementales. Vamos a ver que el eje menor de la elipse es un eje de simetría.
INVESTIGA
Trata de probar el resultado antes de continuar leyendo. Se necesitan sólo Matemáticas elementales.
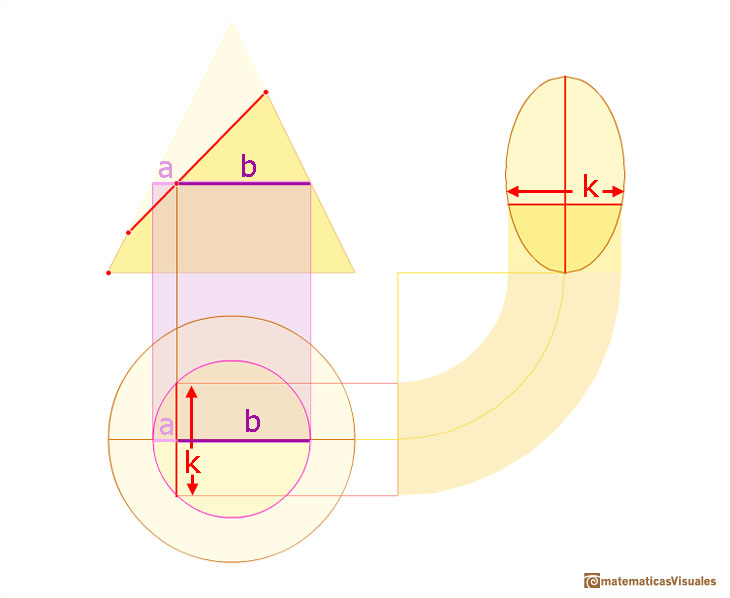
En primer lugar, para cada punto del eje major necesitamos calcular k, el ancho de la elipse en ese punto.
Nos puede ser útil revisar el concepto de media geomérica de dos número. He usado esa idea al estudiar la esfera.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.
Ahora, consideramos dos puntos simétricos del eje mayor de la elipse.
Debemos probar que
O, simplemente
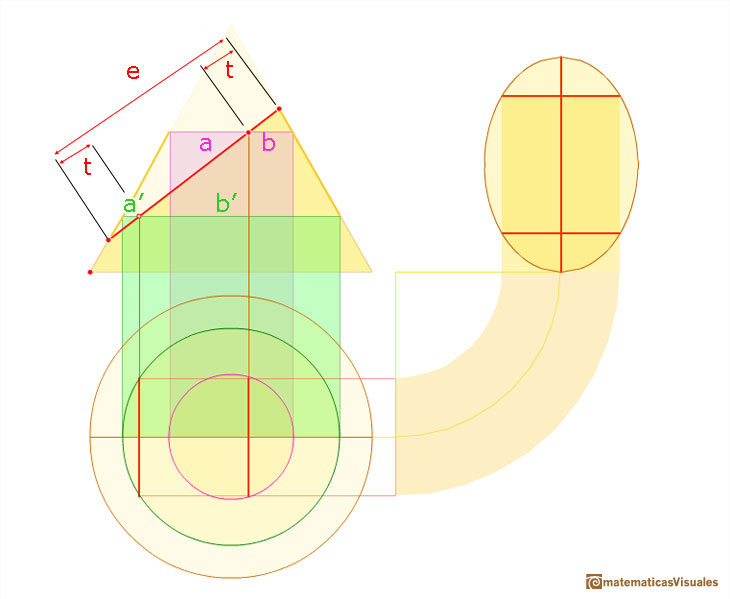
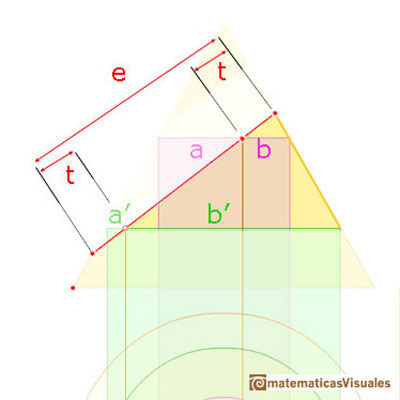
En la siguiente imagen hay señalados dos triángulos semejantes.
Then
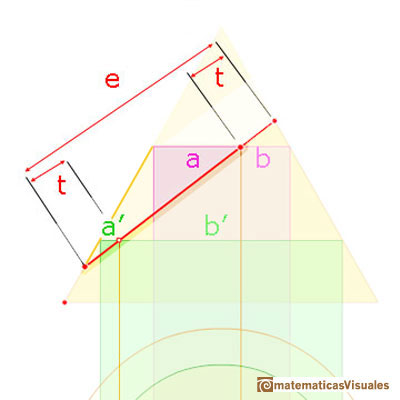
Aquí podemos ver otros dos triángulos semejantes.
Y podemos escribir
Combinando estas dos igualdades
Entonces
Y esto es lo que queríamos probar.
REFERENCIAS
Erwin Panofsky, The Life and Art of Albrecht Dürer.
C. Stanley Ogilvy, Excursions in Geometry. Oxford University Press.
Tom Apostol, Calculus. John Wiley and Sons, 1967.
Dan Pedoe, Geometry and the Visual Arts. Dover Publications.
 SIGUIENTE
SIGUIENTE

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
 ANTERIOR
ANTERIOR

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
MÁS ENLACES

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.
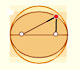
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
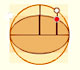
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
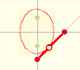
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.
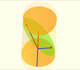
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
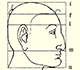
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
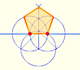
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.
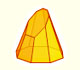
Desarrollos planos de pirámides truncadas por un plano oblicuo.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera



 ANTERIOR
ANTERIOR
























 SIGUIENTE
SIGUIENTE




