En su libro 'Sobre conoides y esferoides', Arquímedes calcula el área de una elipse (Proposición 4)

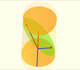
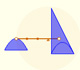
Cuando contraemos verticalmente una circunferencia obtenemos una elipse. Una elipse tiene un semieje mayor y un semieje menor.

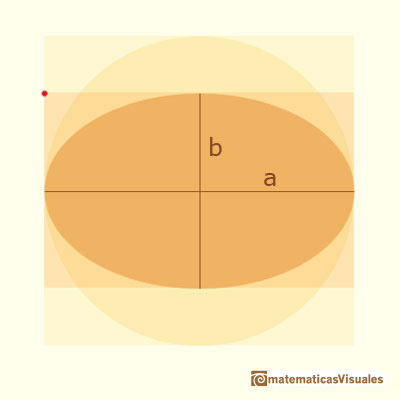
La fórmula del área de una elipse es una generalización de la fórmula del area de un círculo. El área de una elipse con semiejes mayor y menor a y b es:

En primer lugar vamos a deducir esta fórmula usando una aproximación intuitiva. Esta aproximación intuitiva tendrá que ser demostrada rigurosamente después. Arquímedes tiene clara esta distinción entre el 'Método' de descubrir resultados y una prueba rigurosa de un teorema. Podemos ver un ejemplo del 'Método' de Arquímedes en Arquímedes: el área de un segmento parabólico.

Una vez que obtenido el resultado veremos cómo Arquímedes lo demostró.

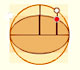
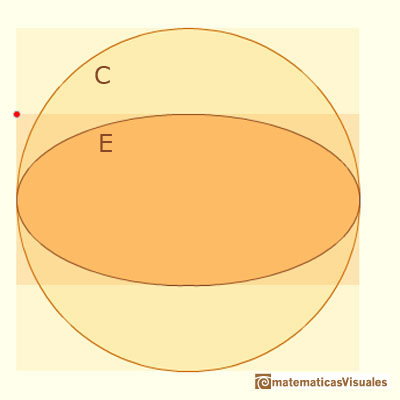
La circunferencia de radio a, circunscrita a la elipse se llama su circunferencia auxiliar. Si estrechamos verticalmente la circunferencia obrenemos la elipse. Un punto m in la elipse verifica la relación:

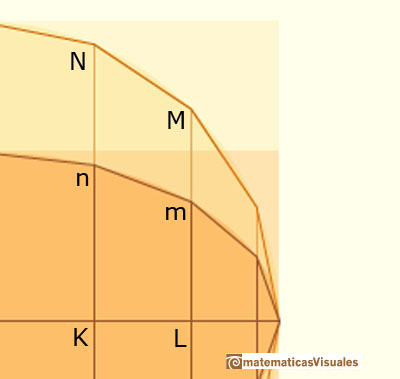
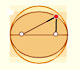
Arquímedes consideró algunos polígonos inscrito en la elipse y en la circunferencia auxiliar. Estos polígonos tienen un número de lados múltiplo de 4 y con dos vértices en los extremos del diámetro horizontal.

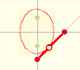
El polígono, P', inscrito en la circunferencia es un polígono regular y P es el polígono inscrito en la elipse E cuyos vértices son las intersecciones con E de las perpendiculares desde los vértices de P' al eje horizontal de E. Podemos considerar estos polígonos como uniones de triángulos y trapezoides. Debido a la compresión tenemos la relación:

Entonces las dos áreas de estos polígonos P y P' están en la misma proporción:

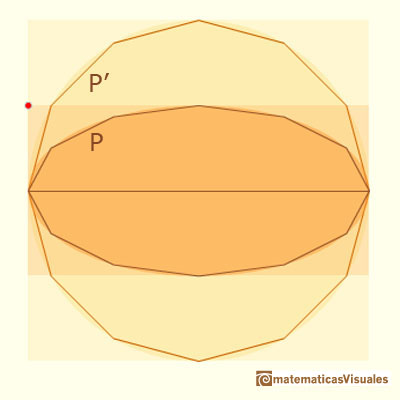
Pero estos polígonos pueden tener tantas caras como queramos y pueden tener sus áreas tan parecidas a las del círculo y la elipse como queramos, entonces podemos aceptar que: (porque 'casi llenan' el círculo y la elipse)

Entonces obtenemos la fórmula del área de la elipse:

Si nuestra intuición es correcta, esta es la fórmula del área de una elipse. Usando el zoon sobre el mathlet podemos ver que la aproximación es muy buena pero que el polígono nunca llena ni la elipse ni el círculo

Esta es una aproximación muy interesante pero Arquímedes necesitaba una prueba lógica y rigurosa. Su demostración no es un ejemplo del uso de la técnica de exhaución de Eudoxo con polígonos inscritos y excritos sino un buen ejemplo del uso típico que hizo Arquímedes de la doble reducción al absurdo.

MÁS ENLACES

Ecuación de la elipse

Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.

Elipsógrafo: un aparato mecánico para dibujar elipses

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.

Elipsógrafo: un aparato mecánico para dibujar elipses (2)

Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.

Elipses como secciones de cilindros: Esferas de Dandelin

La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

Alberto Durero y las elipses: secciones de un cono.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Alberto Durero y las elipses: las elipses tienen dos ejes de simetría.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.

Astroide como envolvente de segmentos y elipses

La astroide es la envolvente de un segmento de longitud constante cuyos extremos se mueven sobre dos rectas perpendiculares. También es la envolvente de una familia de elipses con la propiedad de que la suma de sus ejes es constante.

La astroide es una hipocicloide

La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.

Desarrollos planos de cuerpos geométricos (4): Cilindros cortados por un plano oblicuo

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de cuerpos geométricos (8): Conos truncados por un plano oblicuo

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

El Método de Arquímedes para calcular el área de un segmento parabólico

Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

Kepler: El área de un círculo

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

Durero y transformaciones

Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

La función coseno compleja

La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.