La función coseno compleja: una aproximación geométrica
La función coseno en los reales puede extenderse al campo complejo usando la función exponencial:
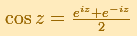
Como la función exponencial es periódica con periodo
,
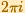entonces la función coseno compleja es periódica, pero con periodo
.
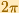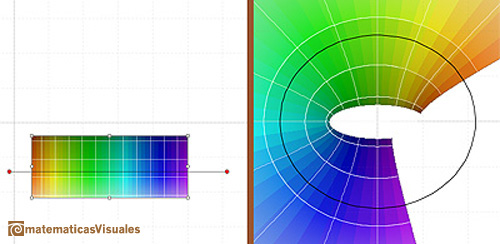
Arrastrando el rectángulo podemos ver cómo la función coseno es periódica.
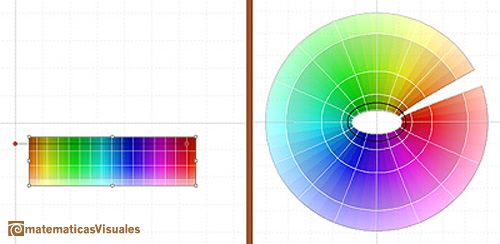
Podemos ver desde otro punto de vista esta periodicidad in la página sobre el Polinomio de Taylor de la función coseno.
La función coseno compleja tiene mucho en común con la función compleja real, por ejemplo:
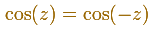
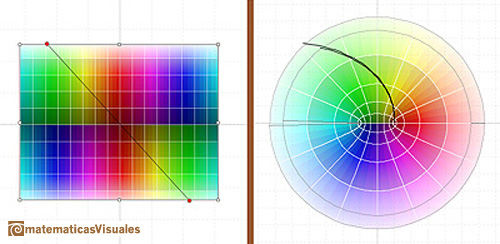
La imagen de una línea horizontal es una elipse:
La imagen de una línea vertical es una hipérbola:
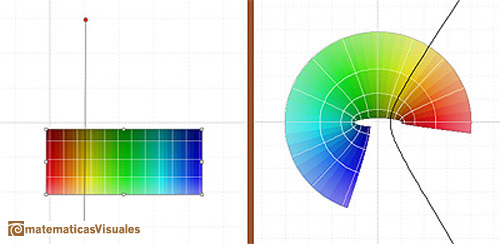
REFERENCIAS
Tristan Needham - Visual Complex Analysis. (pag. 88-89) - Oxford University Press
SIGUIENTE
La función coseno compleja transforma rectas horizontales en elipses cofocales.
ANTERIOR
La función exponencial compleja extiende la función exponencial real al plano complejo.
MÁS ENLACES
Las potencias de exponente natural tienen un cero de multiplicidad n.
Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.
Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.
Un polinomio de grado n tiene n ceros o raíces.
Podemos controlar qué partes del plano complejo se muestran con colores.
Tenemos más control sobre qué partes del plano complejo se representa con colores.
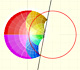
La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.
La inversión preserva la magnitud de los ángulos pero invierte el sentido. Circunferencias ortogonales se transforman en circunferencias ortogonales
El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.
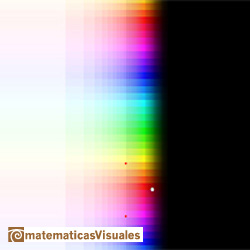
La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.
La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.
Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.