Potencias de exponente natural
Las funciones potencia complejas
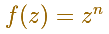
tienen un cero de multiplicidad n en el origen.
Su representación nos permite ver cómo en un cero de multiplicidad n el ciclo de colores se repite n veces.
Podemos modificar el valor de n para ver la representación de diferentes funciones potencia.
ENLACES
|
Polinomio de grado 3
Podemos modificar los tres ceros de este tipo de polinomios.
|
|
Potencias con exponentes naturales
Exploramos unas funciones particularmente sencillas.
|