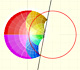
Inversión en una circunferencia es una transformación que preserva la magnitud de los ángulos pero cada ángulo
se transforma en un ángulo de signo opuesto. El sentido o dirección de cada ángulo se invierte.
La inversión en una circunferencia es una transformación anti-conforme (como la reflexión en una recta).
En particular, la inversión es una transformación que preserva el ángulo de intersección de dos circunferencias.
Circunferencias ortogonales (o rectas perpendiculares) se transforman en circunferencias ortogonales (o rectas).
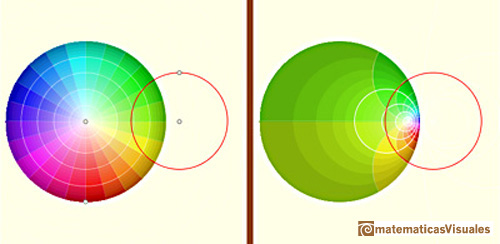
Una circunferencia ortogonal a la circunferencia de inversión se transforma en ella misma (no punto a punto).
Todas las rectas que pasan por un punto y todas las circunferencias concéntricas que tienen ese punto por su centro
común pueden ser vistos como dos casos particulares de haces coaxiales de circunferencias. Estos dos haces coaxiales
son ortogonales. Las rectas forman un haz coaxial secante y las circunferencias concentricas forman un haz coaxial
no secante. Estos haces coaxiales ortogonales se transforman en dos haces coaxiales ortogonales:
Cada rectángulo "pequeño" se transforma en un rectángulo "pequeño":
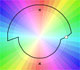
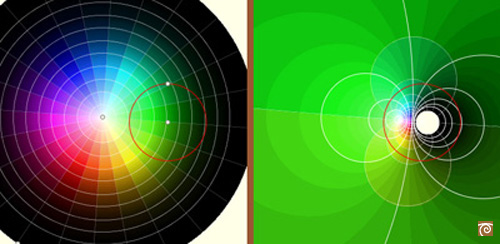
En esta figura podemos ver cómo el orden de colores se invierte (si los miramos en sentido horario pasan a antihorario) y este hecho es consecuencia de la inversión del sentido de los ángulos:
REFERENCIAS
Hilber and Cohn-Vossen - Geometry and the Imagination (pag. 253) - Chelsea Publishing Company
Coxeter - Introduction to Geometry - Wiley and Sons.
Pedoe - Circles, a Mathematical View - Dover
Rademacher and Toeplitz - The Enjoyment of Mathematics (Números y Figuras - Alianza Editorial)
Ogilvy - Excursions in Geometry (pag. 24)- Oxford University Press
MÁS ENLACES

Las potencias de exponente natural tienen un cero de multiplicidad n.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.

Podemos controlar qué partes del plano complejo se muestran con colores.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Tenemos más control sobre qué partes del plano complejo se representa con colores.

La función exponencial compleja extiende la función exponencial real al plano complejo.
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

La función coseno compleja transforma rectas horizontales en elipses cofocales.
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.



 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR