La inversión en una circunferencia es una transformación de los puntos del plano (excepto un punto).
A la circunferencia la llamamos circunferencia de inversión. Consideraremos una circunferencia C de radio r y centro
el punto q.
El centro de la circunferencia de inversión (centro de inversión) no tiene imagen.
Si el centro de la circunferencia de inversión es el origen y el radio es 1 esta transformación tiene una fórmula simple:
En el caso general, la inversión viene determinada por:
Los puntos de la circunferencia de inversión se transforman en ellos mismos y cada punto de dentro de la circunferencia
se transforma en un punto de fuera (y viceversa). Cada punto, su imagen y el centro de la circunferencia están en
la misma recta. A veces, nos referimos a la inversión como reflexión en una circunferencia.
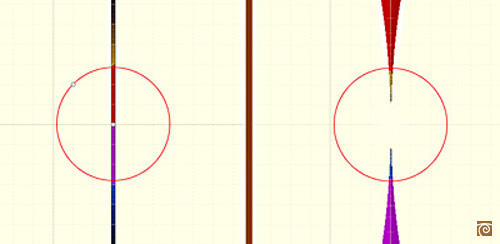
Cada recta que pasa por el centro de inversión se transforma en ella misma.
Cada recta que no pasa por el centro de inversión se transforma en una circunferencia que pasa por el centro de inversión.
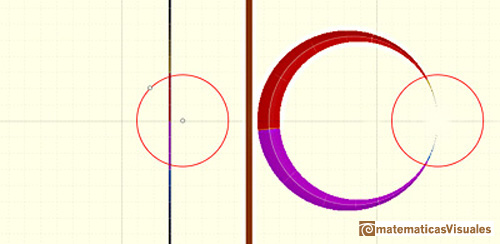
El inverso de una circunferencia es una recta o una circunferencia. Si la circunferencia pasa por el centro de inversión,
su inversa es una recta que no pasa por el centro de inversión.
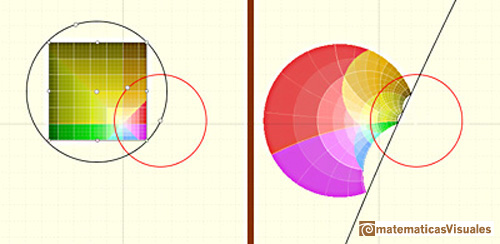
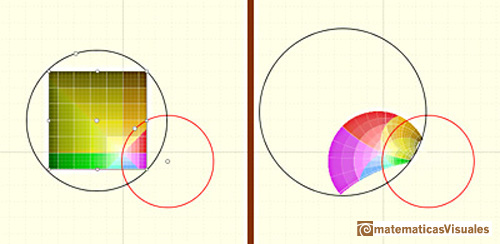
La imagen de una circunferencia que no pasa por el centro de inversión es otra circunferencia que no pasa por el
centro de inversión.
REFERENCIAS
Hilber and Cohn-Vossen - Geometry and the Imagination (pag. 253) - Chelsea Publishing Company
Coxeter - Fundamentos de Geometría - Ed. Limusa
Pedoe - Circles, a Mathematical View - Dover
Rademacher and Toeplitz - Números y Figuras - Alianza Editorial
Ogilvy - Excursions in Geometry (pag. 24)- Oxford University Press
MÁS ENLACES

Las potencias de exponente natural tienen un cero de multiplicidad n.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.

Podemos controlar qué partes del plano complejo se muestran con colores.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Tenemos más control sobre qué partes del plano complejo se representa con colores.

La función exponencial compleja extiende la función exponencial real al plano complejo.
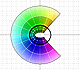
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
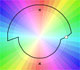
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.

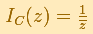
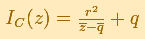
 SIGUIENTE
SIGUIENTE




















 ANTERIOR
ANTERIOR








