
Las transformaciones de Moebius son funciones con fórmula del tipo
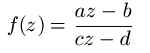
Tiene un cero y un polo simples.
Son transformaciones conformes del plano complejo y transforman "circunferencias" en "circunferencias". Circunferencias entre comillas son circunferencias y rectas.
En esta primera aproximación a estas transformaciones controlamos el cero, el polo y un tercer punto que es fijo por la transformación.
En la representación que llamamos en "polares" los colores se distribuyen según un haz de rectas concurrentes en el origen y una familia de circunferencias concéntricas con centro el origen. En la representación de colores en "cartesianas" los colores forman una cuadrícula. En ambos casos, son dos familias de "circunferencias" ortogonales. Se transforman en dos haces de "circunferencias" ortogonales.
En esta representación sólo se colorean de color no negro los puntos transformados con módulo pequeño. Es decir, se pierde detalle en el polo.
Podemos elegir dos criterios para elegir el color. En polares los colores se distribuyen en sectores y los tonos en círculos concéntricos. En cartesianas los colores forman una cuadrícula. Si marcamos "Identidad" podremos ver estas dos distribuciones.
En polares, podemos optar por colorear sólo aquellos puntos que se transforman en puntos de módulo menor que 1, aquellos que están entre 1 y 2 o ambos. Análogamente, en el caso de "cartesianas".
También podemos representar dos bandas: puntos "muy próximos" a 1 y puntos "muy próximos" a 2.
Podemos mover (despacio) los puntos que representan el cero y el polo y el tercer punto que es fijo.
Pulsando con el botón derecho y arrastrando se puede mover el plano.
REFERENCIAS
Los interesados en las transformaciones de Moebius pueden ver un vídeo muy premiado y muy bonito hecho por Douglas N. Arnold en colaboración con Jonathan Rogness. Una maravilla. Arnold tiene varias páginas sobre visualización matemática, por ejemplo, sobre visualización de Análisis Complejo
Tristan Needham - Visual Complex Analysis. Oxford University Press.
MÁS ENLACES


















 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR







