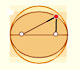
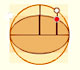
Ya hemos estudiado el elipsógrafo o "trammel" de Arquímedes. Es un aparato que consiste en una varilla que se mueve de modo que dos puntos determinados están sobre dos líneas perpendiculares.
Ya sabemos que cada punto de esa varilla describe una elipse.
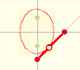
Si consideramos la envolvente de un segmento de longitud constante que se mueve con sus extremos sobre dos rectas perpendiculares (una escalera que se desliza apoyada sobre el suelo y una pared vertical) el resultado es una curva que tiene cuatro cúspides y que se llama astroide.
También hemos visto que la astroide es la envolvente de una familia de elipses que tienen la propiedad de que la suma de sus ejes es una constante (la longitud del segmento móvil).
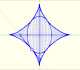
Pero la astroide se suele definir de otro modo. Se define la astroide como el lugar geométrico de un punto P en una circunferencias que rueda sin deslizar dentro de una circunferencia que tiene el radio cuatro veces mayor.
Por esta manera de generar la astroide decimos que es un tipo de hipocicloide. Una hipocicloide es una curva plana generada por un punto fijo en una circunferencia que rueda dentro de otra circunferencia mayor.
Si la circunferencia pequeña tiene radio r y la grande tiene radio 4r la curva tiene cuatro cúspides. Se parece a la envolvente de la "escalera que se desliza", del "trammel" de Arquímedes. Pero, ¿es la misma curva?. Tenemos que probarlo (siguiendo a Apostol y Mnatsakanian) y usaremos razonamientos elementales.
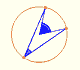
El punto P rueda sin deslizar. Los dos arcos circulares CL y CP tienen la misma longitud. El ángulo central de la circunferencia pequeña es cuatro veces el ángulo central de la circunferencia grande (porque el radio de la grande es cuatro veces el de la pequeña).
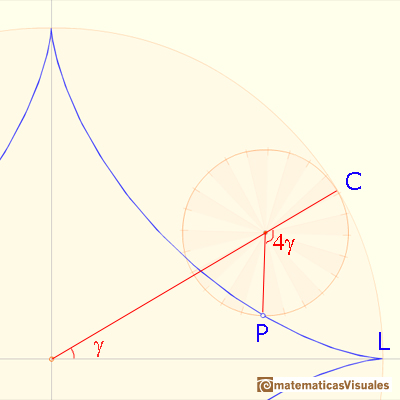
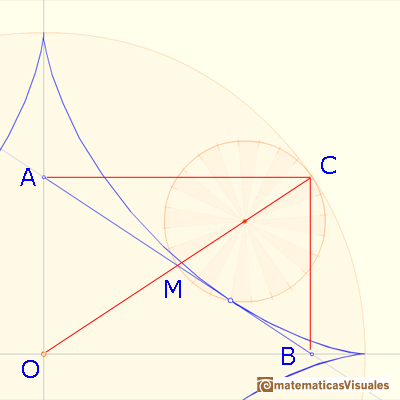
¿Cómo podemos dibujar la tangente a la astroide por P?. Queremos probar que el segmento AB tiene una longitud fija. Si podemos mostrar que la longitud de AB no cambia conforme P se mueve describiendo la astroide, entonces habremos probado que AB es la varilla del elipsógrafo (un "trammel").
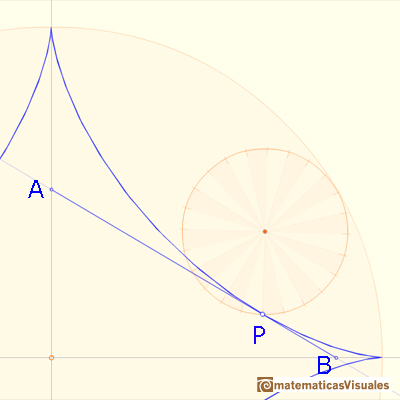
M es el punto medio de OC. La recta AB dibujada por PM, perpendicular a CP, es también tangente a la astroide por P porque C es el centro de rotación instantánea de la circunferencia pequeña al rodar dentro de la circunferencia grande.
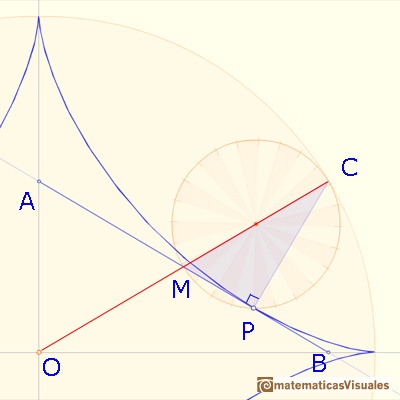
Para probar que la longitud de AB no varía conforme P se mueve a lo largo de la astroide podemos mostrar que M es también el punto medio de AB, y que el triángulo OMA es isósceles.
Usando la propiedad de los ángulos central e inscritos:
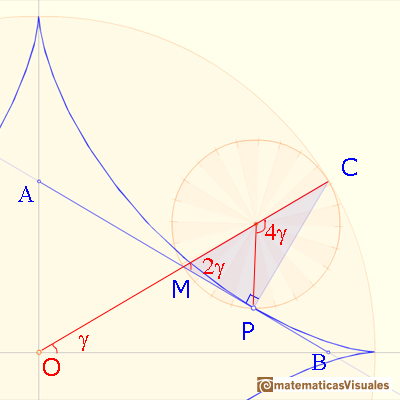
Una recta horizontal a través de M biseca el ángulo CMA como se muestra aquí:
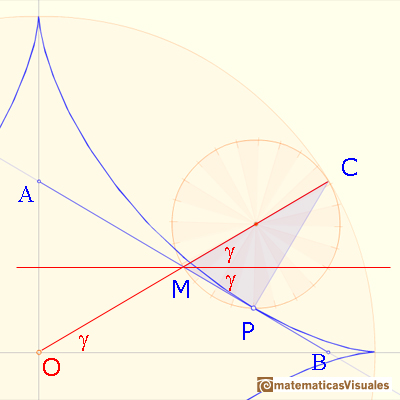
Entonces el triángulo OMB es isósceles:
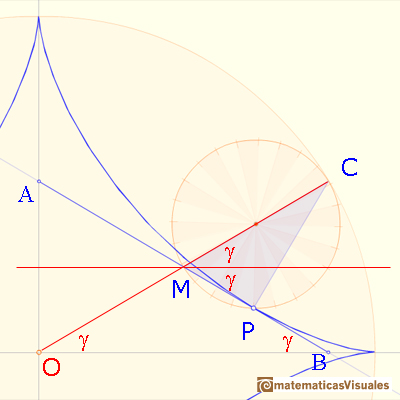
El triángulo OMA es también isósceles. Entonces AB tiene una longitud fija, y ya hemos visto que es siempre tangente a la astroide.
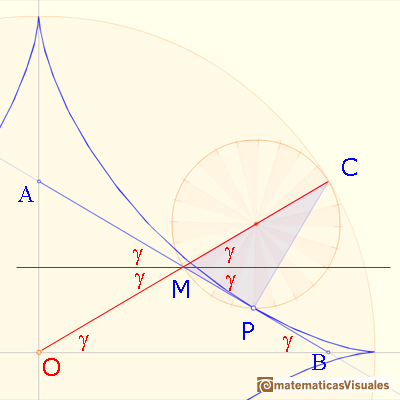
Y así concluyen Apostol y Mnatsakanian este apartado: "La envolvente de un 'trammel' (de la varilla de un elipsógrafo) de longitud fija es una astroide".
REFERENCIAS
 ANTERIOR
ANTERIOR
MÁS ENLACES