Ya hemos estudiado el elipsógrafo (o "Trammel" de Arquímedes) y sabemos que cualquier punto de la varilla que se mueve traza una elipse.

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
En esta página nos vamos a fijar sólamente en el segmento de longitud fija cuyos extremos se mueven a lo largo de dos ejes perpendiculares.
A veces pensamos en esta situación como si fuera una escalera de mano que se desliza apoyada en una pared y el suelo.
Siguiendo a Tom Apostol y a Mnatsakanian vamos a ver otra demostración de que cada punto del segmento dibuja una elipse.
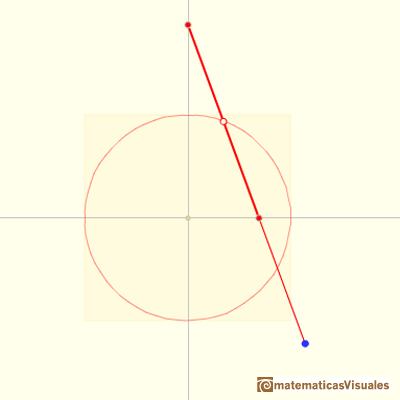
Vamos a empezar por el caso más sencillo: el punto medio del segmento M traza una circunferencia:
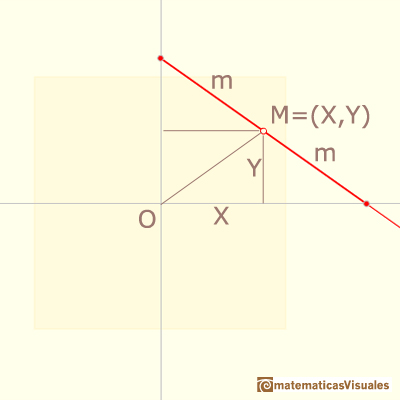
Consideramos las coordenadas del punto medio M de un segmento de longitud 2m.
OM y las dos perpendiculares desde M a los ejes dividen el triángulo rectángulo grande en cuatro triángulos rectángulos congruentes
más pequeños, entonces:
El punto M, conforme se mueve el segmento, traza una circunferencia con centro O y radio m.
Las coordenadas de M cumplen:
Esta es la ecuación cartesiana de una circunferencia.
Podemos escribir esta ecuación para destacar que la circunferencia es un caso especial de elipse:
Un poco más adelante volveremos a usar esta ecuación.
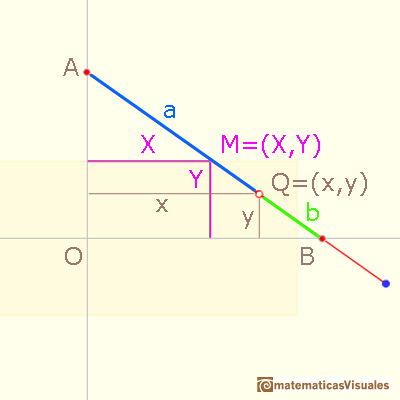
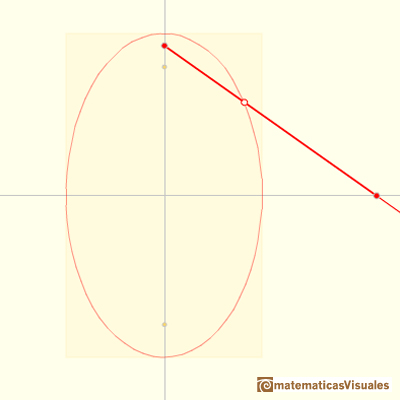
Consideremos ahora otro punto Q del segmento
Q divide al segmento en dos partes de longitud a y b.
Usando semejanza de triángulos podemos relacionar las coordenadas de
Q con las del punto medio M:
Usando la fórmula de la circunferencia como caso particular de elipse
podemos probar que las coordenadas de Q
cumplen la ecuación
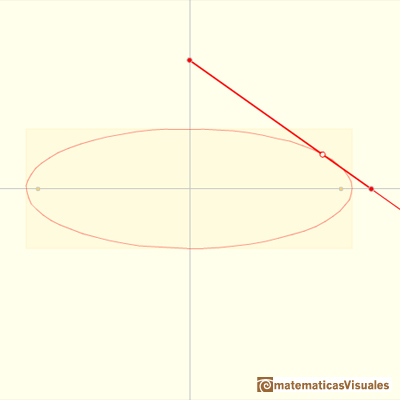
y, por lo tanto, el punto Q describe una elipse.
Este mismo razonamiento sirve para cualquier punto Q del segmento (incluso si Q está en la recta, fuera del segmento).
En todos los casos:
Los semiejes de la elipse son las distancias desde Q a los extremos del segmento.
REFERENCIAS
Tom Apostol and Mamikon Mnatsakanian, 'New Horizons in Geometry' (Chapter 9. Trammels), Mathematical Association of America, 2012.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Hilbert and Cohn-Vossen, Geometry and the Imagination. Chelsea Publishing Company. pag.278.
Robert C. Yates, 'A Handbook on curves and their properties', J.W.Edwards-Ann Arbor, 1947.
J.L. Coolidge, The Mathematics of great Amateurs. Second Edition. Claredon Press. Oxford. Jan de Witt's proof in page 124.
MÁS ENLACES
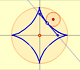
La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.
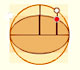
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
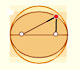
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
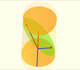
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
Desarrollos planos de pirámides truncadas por un plano oblicuo.

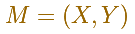
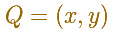
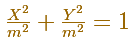
 SIGUIENTE
SIGUIENTE























 ANTERIOR
ANTERIOR


