Arquímedes nació en Siracusa (una ciudad griega en Sicilia) alrededor del 287 aC y fue asesinado en el 212 aC cuando Siracusa fue conquistada por Roma durante la II Guerra Púnica.

"Entre sus más famosos resultados están el cálculo del volumen y de la superficie esférica y el área del segmento parabólico. Arquímedes descubrió estos resultados usando métodos no rigurosos y después los confirmó con el método de exhausción." (Stillwell)

En su trabajo "El Método", Arquímedes escribió sobre su método de descubrimiento. El "método mecánico" de Arquímedes se basa en la ley de la palanca. "En él, Arquímedes muestra el método que presumiblemente usó para obtener mucha de sus conclusiones en problemas sobre áreas y volumenes. Dándose cuenta de que es muy ventajoso tener una noción preliminar del resultado antes de llevar a cabo la demostración geométrica deductiva, Arquímedes empleó para este propósito, junto con su ley de la palanca, la idea de una superficie como formada por líneas." (Boyer)

Aquí intentamos mostrar como Arquímedes descubrió el área de un segmento parabólico.

El área de un segmento parabólico es 4/3 el área del triángulo que tiene la misma base y vértice.

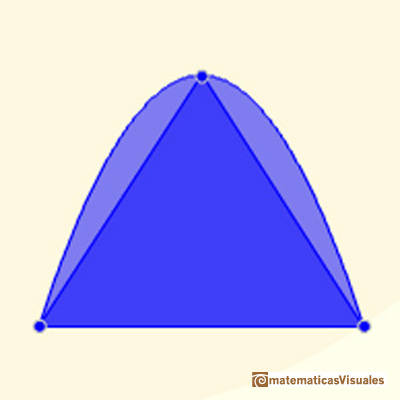
Considró un segundo triángulo usando una tangente. Este triángulo es 4 veces el primero. Y el área de este segundo triángulo resulta ser 1/3 el área del segmento parabólico.

El segmento parabólico y este segundo triángulo estarán en equilibrio pero uno de los brazos de la balanza será tres veces más largo: The parabolic segment and the second triangle will be in equilibrium:

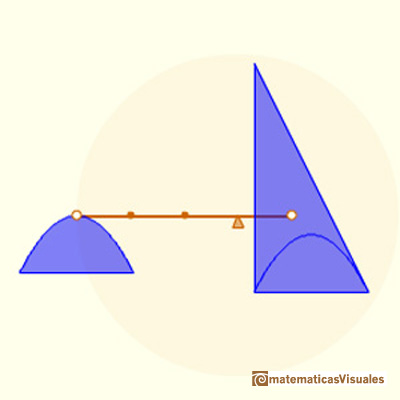
La construcción de Arquímedes es más general que la que mostramos aquí. Podemos leer la explicación en el libro de Boyer:

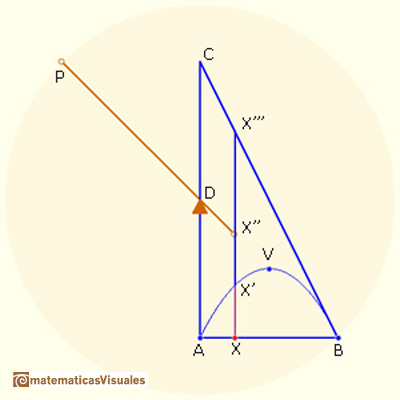
"V es el vértice de la parábola, BC es tangente en B, BD = DP, y X es cualquier punto en AB, sabemos por las propiedades de la parábola que para cualquier posición de X tenemos la proporción"

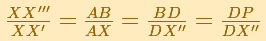
Pero X'' es el centro de gravedad de XX''', por lo tanto, por la ley de la palanca, vemos que XX', si lo llevamos hasta P como su punto medio, equilibrará XX''' en su posición actual. Esto será verdad para cualquier posición de X en AB. Además, como el triángulo ABC consiste en los segmentos XX''' en el triángulo y como el segmento parabólico AVB también está formado por las líneas XX', concluímos que el triángulo ABC en su situación actual estará en equilibrio en D con el segmento parabólico cuando éste sea llevado a P como su centro de gravedad. Pero el centro de gravedad de ABC está en BD y está a 1/3 de la distancia desde D a B, por lo tanto el segmento AVB es 1/3 el triángulo ABC o 4/3 el triángulo AVB. (Boyer)

ENLACES

	Kepler: El área de un círculo Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.
	Kepler: Superficie y volumen de una esfera Kepler estudió el volumen y la superficie de una esfera. La esfera puede considerarse formada por conos cuya altura es el radio de la esfera. Entonces el volumen de la esfera será la suma de todos esos conos. Así obtiene la relación entre la superficie de la esfera y su volumen.
	Kepler: El volumen de un barril de vino Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes.
	Kepler: Las proporciones óptimas de un barril de vino Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.
	Cavalieri: El volumen de una esfera Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera
	Sorprendente congruencia Cavalieri entre una esfera y un tetraedro Se muestra la esfera y el tetraedro de Howard Eves con sus correspondientes secciones congruentes.
	Integral de potencias La integral de las funciones potencia era conocida por Cavalieri.
	El teorema de Pitágoras en un mosaico Podemos ver el teorema de Pitágoras en un mosaico.