Howard Eves recibió el premio George Polya por el artículo Two Surprising Theorems on Cavalieri Congruence (Dos teoremas sorprendentes sobre la Congruencia de Cavalieri).
En ese artículo, Eves escribe una breve reseña sobre Cavalieri (1598-1647): "Cavalieri fue uno de los matemáticos más influentes de su tiempo, y el autor de varios trabajos sobre trigonometría, geometría, óptica, astronomía y astrología. Fue de los primeros en reconocer el gran valor de los logaritmos y fue, en gran medida, responsable de su introducción en Italia. Pero su mayor contribución a las matemáticas fue un tratado, Geometria indivisibilibus, publicado por primera vez en 1635, dedicado al método de los indivisibles." (Una técnica de cálculo de áreas y volúmenes anterior a la invención del Cálculo).
"El tratado de Cavalieri sobre el método de los indivisibles no está escrito claramente y no es fácil comprender precisamente lo que Cavalieri quiere decir por 'indivisible'. Parece que un indivisible de una superficie plana dada es una cuerda de esa superficie y que una supervicie puede considerarse que está formada por infinitos indivisibles paralelos. De modo semejante, parece que un indivisible de un sólido dado es una sección plana de ese sólido y que un sólido puede considerarse formado por un conjunto de infinitos de esos indivisibles paralelos. Entonces, argumenta Cavalieri, si desplazamos cada uno de esos indivisibles paralelos de una superficie sobre su eje de modo de que extremos de los indivisibles todavía formen una frontera continua, entonces el área de esa nueva superficie así formada es la misma que la de la superficie original, siempre que las dos superficies esten formadas por los mismos indivisibles. Un desplazamiento semejante de los miembros del conjunto de indivisibles paralelos de un sóldo dado darán lugar a otro sólido que tendrá el mismo volumen que el original." (H. Eves)
"Si aceptamos los principios de Cavalieri como intuitivamente evidentes podemos resolver muchos problemas de medida que normalmente requieren técnicas avanzadas del Cálculo. Definamos dos superficies planas que pueden ser colocadas de modo que se corten por segmentos iguales en cada miembro de la familia de líneas paralelas, o dos sólidos que pueden colocarse de modo que intersecan secciones de igual área en cada miembro de la familia de planos paralelos como congruentes Cavalieri. Para encontrar la ára desconocida de uns superficie plana, o el volumen desconocido de un sólido, lo que tenemos que encontrar es una figura con la que podamos comparar, de la que sepamos calcular el área o el volumen fácilmente y que sea congruente Cavalieri con la figura dada." (H. Eves)

Uno de los propósitos del árticulo de Eves es probar algo que es difícil de creer, que existe un poliedro que es congruente Cavalieri con una esfera dada. "!Una esfera es tan redonda y un poliedro tan angular y formado por nada más que planos! Sin embargo, probaremos que existe un poliedro (en realidad, un tetraedro) que es Cavalieri congruente con la esfera dada." (H. Eves)
Ya hemos visto que las áreas de las secciones de la esfera son:

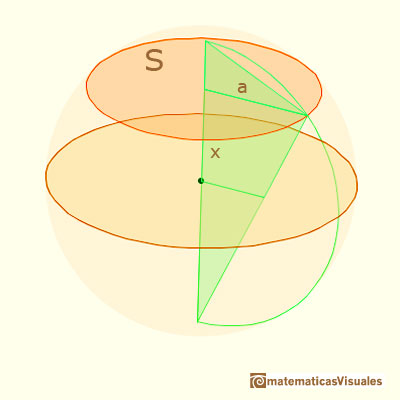
Las correspondientes áreas del tetraedro de Eves son iguales:
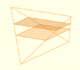
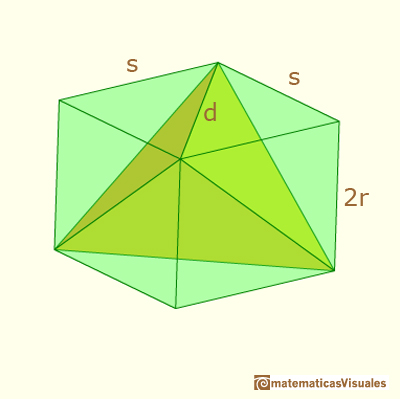
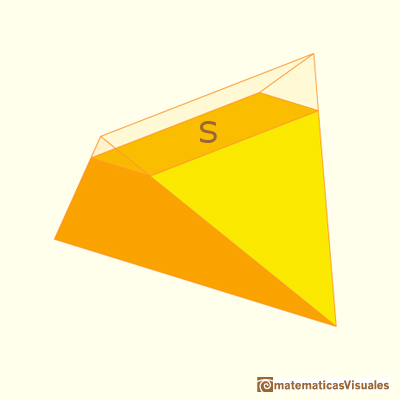
El volumen del tetraedro de Howard Eves es:

Entonces, Eves afirma que:
"Teorema 2. Existe un tetraedro Congruente Cavalieri con una esfera dada."
Por lo tanto, el volumen de la esfera es el mismo que el del tetraedro:
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES