Las funciones potencia fueron el primer tipo de funciones que se pudieron integrar.
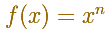
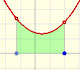
Lo que se pretende es calcular el área bajo la gráfica de una función potencia.
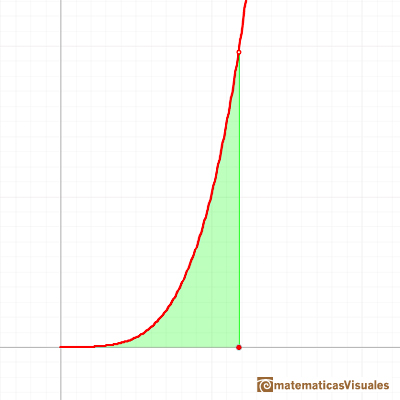
Usando notación moderna escribimos:
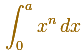
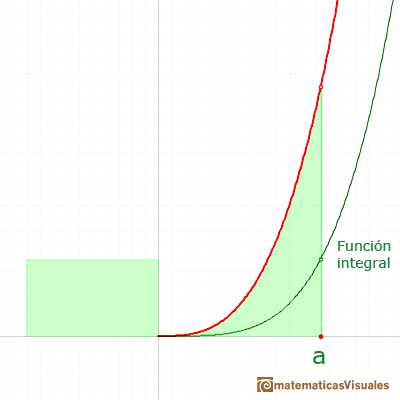
Este problema fue resuelto antes del trabajo de Newton y Leibniz, es decir, antes de que los matemáticos entendieran la relación entre integración y derivadas. Después de la invención del Cálculo, lo que ahora se conoce como el Teorema Fundamental del Cálculo, la respuesta es muy sencilla y es un buen ejemplo de la potencia de esas nuevas herramientas. Sin ellas el problema no es tan simple.
Vamos a ver algunas aproximaciones al problema previas a Newton y Leibniz y como pudo resolverse con ingenio.
Después de la cuadratura de un segmento de parábola por Arquímedes (que murió el 212 aC), Cavalieri (hacia 1630) fue el primero que tuvo un éxito en una cuestión semejante. Después de Cavalieri, otros matemáticos, como Torricelli, Roberval, Wallis y Fermat, trabajaron y resolvieron el problema completamente.
La principal idea que siguieron tanto Arquímedes como Cavalieri, Torricelli, Fermat y otros (varios años antes de Newton, Leibniz, Cauchy o Riemann) fue dividir el intervalo de integración en rectángulos muy delgados y calcular el área sumando el área de todos esos rectángulos.
Cavalieri dividió el intervalo en partes iguales y fue capaz de calcular la integral hasta el caso n=9. Un éxito si tenemos en cuenta las dificultades a las que tuvo que enfrentarse. (Toeplitz pp. 52, Edwards pp. 106-113).
La cuadratura de curvas de la forma y=xk, con k no necesariamente un número natural fue atacada sistemáticamente por John Wallis (1616-1703). Los exponentes racionales y negativos fueron introducidos por él (1655). Wallis tuvo una influencia decisiva en el desarrollo matemático del joven Newton.
En esta página vamos a seguir el procedimiento que siguió Fermat para resolver esta integral para n un número natural (es el caso más sencillo y, además, vamos a utilizar notación moderna). El mismo argumento, con cambios menores, funciona cuando el exponente es un número racional positivo. Fermat pudo resolverlo para un exponente arbitrario (excepto el caso importante n=-1) en uno de us últimos trabajos. Su 'Tratado sobre Cuadraturas' (1659) apareció demasiado tarde para tener un profundo efecto en el desarrollo del cálculo.
La idea de Fermat es una aplicación bonita y no trivial de la suma de una serie geométrica.
Tendremos que recordar como se suma una serie geométrica:
Más tarde vamos a usar la siguiente factorización de un polinomio (podemos ver que está relacionada con la suma de una progresión geométrica finita):
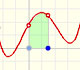
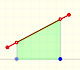
Fermat empieza diviendo el intervalo de integración [0,a]. Pero no lo hace en subdivisiones iguales, usa subdivisiones crecientes determinadas por una progresión geométrica. Así determina la base de los rectángulos.
Sea r un número entre 0 y 1, entonces:
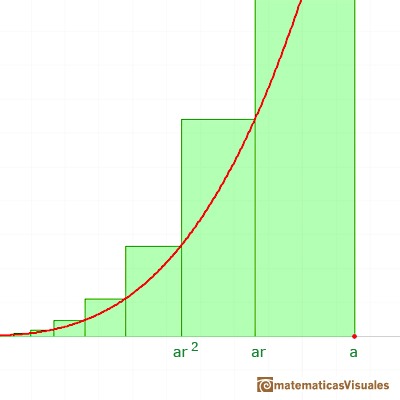
Considera rectángulos con base:
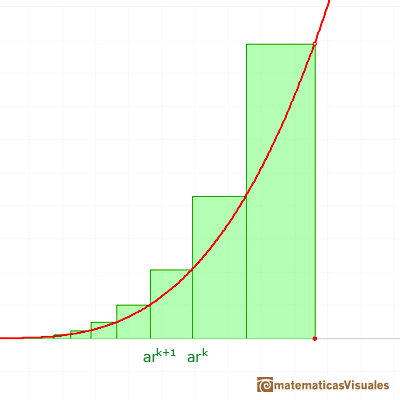
La anchura de estas bases están en progresión geométrica.
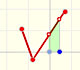
La altura de cada rectángulo es:
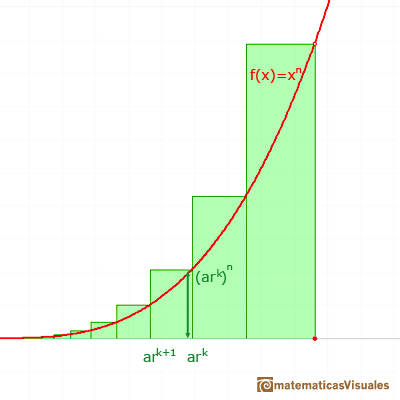
Por lo tanto, el área de cada rectángulo es:
Las áreas también están en progresión geométrica.
Podemos sumar todos estos rectángulos (el resultado dependerá del valor de r):
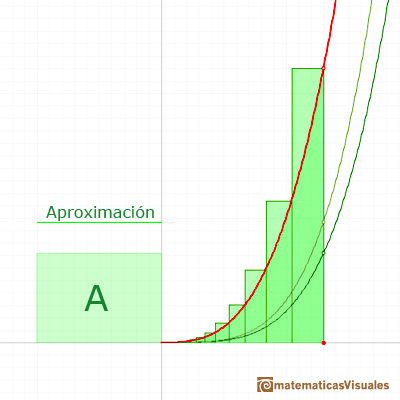
Sabemos como sumar una serie geométrica:
Vamos a usar ahora por primera vez el que n es un número natural y podemos simplificar la expresión:
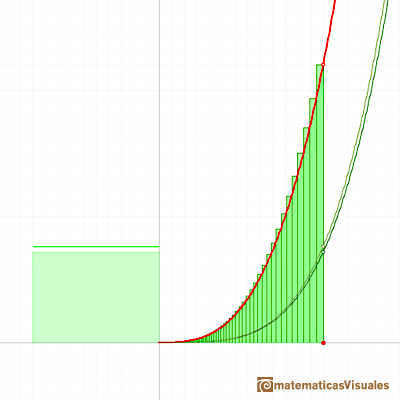
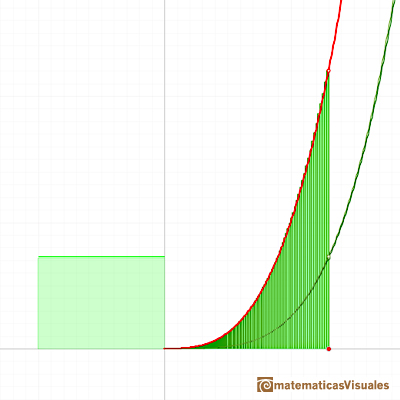
Cuando la razón r se aproxima a 1 el denominador de esta expresión se aproxima a n+1 y podemos concluir con el resultado:
Un argumento muy parecido nos permite justificar la integral de funciones potencia cuando el exponente es el inverso de un número natural:
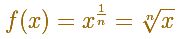
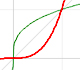
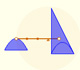
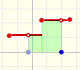
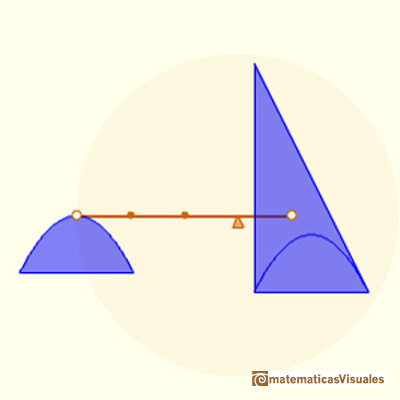
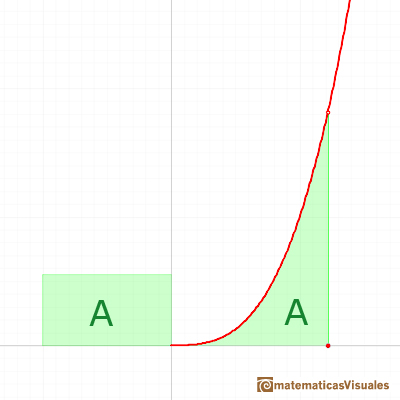
El caso anterior se puede deducir de un modo muy intuitivo a partir de la siguiente imagen:
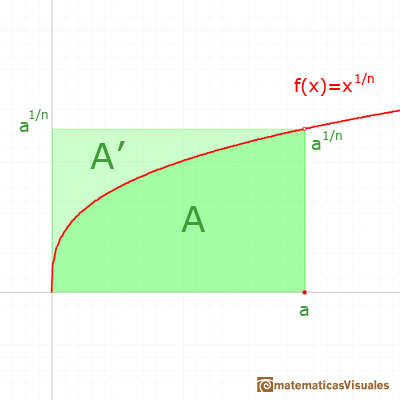
Girando la figura, la función puede verse como xn y esta función la sabemos integrar, es decir, podemos calcular A'. También sabemos calcular el área de todo el rectángulo, luego fácilmente podremos deducir A.
Más general, usando progresiones geométricas podríamos justificar el caso cuando el exponente es un número racional positivo cualquiera como hizo Fermat, es decir, la función que se trata de integrar es:
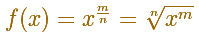
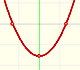
Fermat fue capaz de integrar funciones potencia con exponentes positivos y negativos (excepto para el caso importante n=-1). Este caso, el de la hipérbola equilátera está relacionado con la función logarítmica.
Un punto de vista de Boyer sobre Fermat: "En estas cuadraturas vemos la mayoría de os aspectos esenciales de la integral definida - la división del área bajo la curva en pequeños elementos de área, la aproximación numérica de la suma por medio de esos rectángulos y la ecuación analítica e la curva, y finalmente un intento de Fermat de expresar el equivalente de lo que llamaríamos el límite de esa suma, conforme el número de elementos aumenta indefinidamnete y el área de cada uno de ellos se hace indefinidamente pequeña. Uno está casi tentado de decir que Fermat reconoció todos los aspectos excepto el de la propia integral; es decir, no reconoció la operación implicada como significativa en sí misma. El procedimiento fue para él, como había sido para todos sus predecesores, simplemente el de encontrar una cuadratura -contestar una cuestión geométrica específica. Solo con Newton y Leibniz el proceso involucrado en consideraciones infinitesimales fue reconocido como operaciones, independientemente de cualquier consideración geométrica o física." (C. Boyer, pp.161-162)
El resumen de Edwards: "Durante las décadas centrales del siglo diecisiete, se aplicaron técnicas con infinitesimales o indivisibles, motivadas por intentos de relajar el rigor del método clásico de exhausción, para establecer el resultado básico de cuadratura"
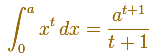
Fue el resultado en sí mismo, más que los métodos particulares usados para obtenerlo, lo que tuvo importancia duradera. Porque hacia 1660 estos primeros métodos directos de cuadratura se fueron haciendo obsoletos rápidamente y pronto fueron superados por métodos indirectos basados en la relación entre los métodos de cuadratura y los métodos de obtención de tangentes." (C.H. Edwards, pp. 120-121)
Archimedes, Cavalieri, Fermat, Torricelli, Wallis and others worked wery hard to integrate power functions. But these integrals are very easy to solve after the discoveries of Newton and Lebiniz (as an application of what nowdays is known as the
Arquímedes, Cavalieri, Fermat, Torricelli, Wallis y otros tuvieron que trabajar mucho para encontrar procedimientos para calcular integrales de funciones potencia. Pero estas integrales son muy sencillas de resolver tras los descubrimientos de Newton y Leibniz (como una aplicación sencilla de lo que ahora conocemos como el Teorema Fundamental del Cálculo)
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES