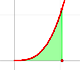
¿Qué funciones acotadas son integrables?
Esta es una pregunta difícil de responder. Pero una respuesta parcial y simple es que las funciones monótonas son integrables.
Una función es monótona en un intervalo si es creciente o decreciente en el intervalo.
Si f es una función monótona en [a,b] entonces es acotada e integrable. (Y este resultado se puede generalizar fácilmente a
funciones acotadas monótonas a trozos [ver Ross, p. 196])
"Afortunadamente, muchas de las funciones que ocurren en la práctica son monótonas o suma de funciones monótonas, por lo tanto este
pequeño resultado tiene mucha aplicación."
(Apostol, p. 76)
En el applet podemos jugar con un caso simple de funciones monótonas: funciones monótonas continuas, pero el resultado es verdadero en general.
(De paso podemos decir que otra familia importante de funciones integrables son todas las funciones continuas en [a,b]).
Podemos modificar la curva, los extremos de integración, aumentar o disminuir el número de rectángulos, ver el error que hacemos y una cota de
ese error. Podemos ver una animación sobre esto.
Antes de considerar aspectos más teóricos del problema podemos pensar un poco sobre la aproximación del valor de la integral definida de una
función monótona.
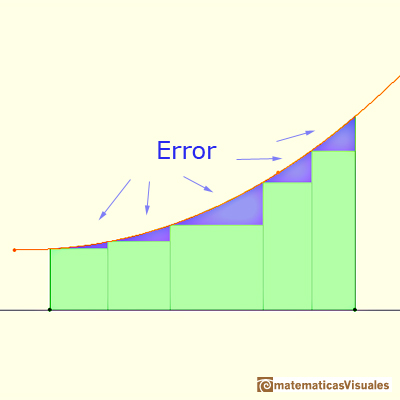
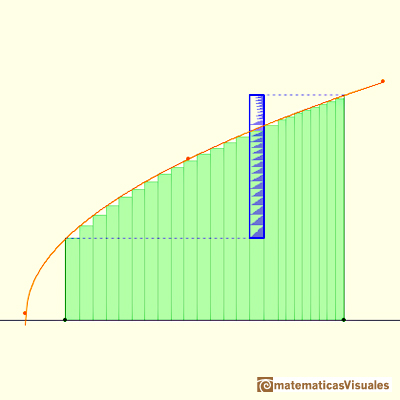
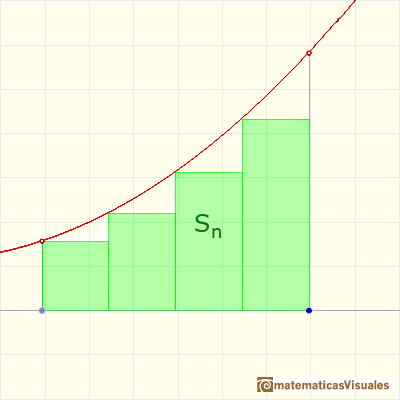
Cuando aproximamos una integral usando rectángulos cometemos un error.
En algunos casos, por ejemplo, con funciones monótonas, podemos acotar la magnitud del error.
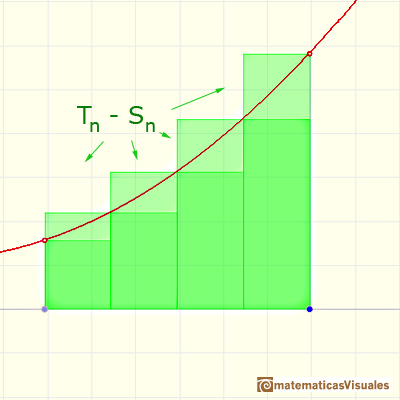
El error es igual a la suma de las áreas de los "triángulos curvos" azules.
Este error es menos que el área de un rectángulo.
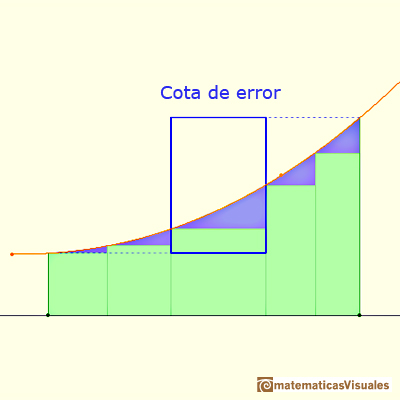
Si consideramos un caso simple, cuando las bases de los rectángulos son iguales, entonces podemos calcular una cota de error:
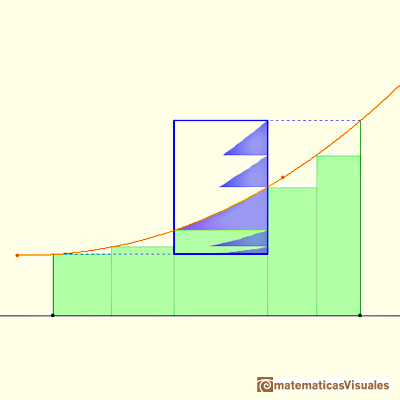
Usando particiones refinadas podemos obtener cotas de error tan pequeñas como queramos, pues cuando refinamos una partición la base de los rectángulos es menor.
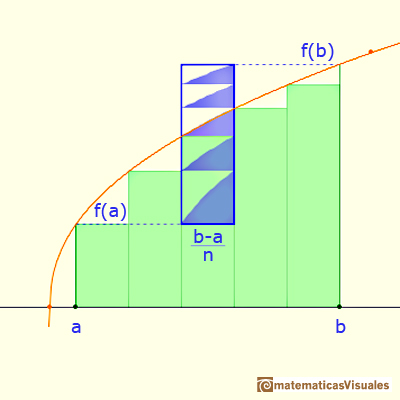
Vamos a probar que una función monótona positiva y creciente en [a,b] es integrable.
Empezamos con una partición del intervalo:
Si dividimos el intervalo en n partes iguales entonces la base de cada rectángulo es:
Podemos calcular una cota de error superior de la integral:
Consideramos la sucesión decreciente
Con la misma partición, esta es una cota inferior de la integral:
Consideramos la sucesión creciente
Si estas dos sucesiones convergen hacia el mismo límite, podemos considerar ese límite como la integral definida y escribir
Entonces la cuestión es si realmente convergen.
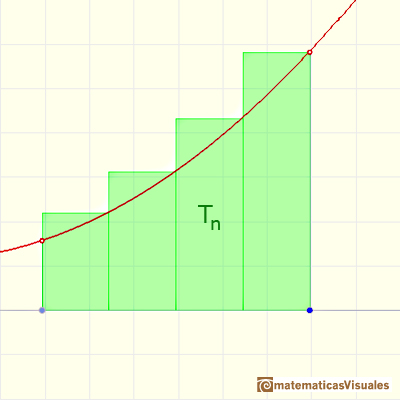
Cuando consideramos una funcion monótona creciente tenemos una sucesión creciente (Sn) y
una sucesión decreciente (Tn). Entonces tenemos que comprobar que
Calculamos Tn - Sn
Entonces el límite
Concluímos que si f es mónotona en el intervalo [a,b], entonces la integral definida existe. [Toeplitz, p.64]
REFERENCIAS
Markushevich, Áreas y logaritmos. Ed. Mir.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc. (p. 77).
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc. (p. 256)
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963 (p. 63).
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980 (p. 190).
MÁS ENLACES

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.

Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.
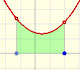
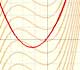
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
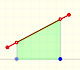
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.
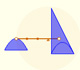
Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

Kepler fue uno de los matemáticos que contribuyeron al origen del cálculo integral. Uso técnicas infinitesimales para calcular áreas y volúmenes.

Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).

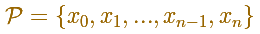
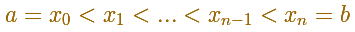
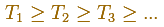
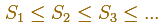
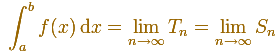
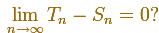
![Integral definida de funciones monótonas: si f es mónotona en el intervalo [a,b], entonces la integral definida existe | matematicasVisuales](../../../images/analysis/integral/integralCota/formula/integralCota7.gif)

 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR