Vamos a estudiar las funciones constantes a trozos o funciones escalonadas.
Aunque estas funciones son sencillas son muy importantes: las podemos usar para aproximar otras funciones más complejas y nos pueden ayudar a comprender mejor el Teorema Fundamental del Cálculo desde un punto de vista muy básico. Como un ejemplo de cómo usar estas funciones para definir el concepto de integral se puede ver el libro de Tom Apostol.
Alguna de las ideas y de los ejemplos de esta página los he tomado de dos artículos muy intersantes de Gilbert Strang y Antony J. Macula.
Una función definida a trozos es una función que está determinada por varias subfunciones. Cada subfunción se aplica sobre un subdominio del dominio de la función. En estas páginas, estos subdominios serán intervalos. Podemos decir que estas funciones se comportan de modo diferente dependiendo del valor de entrada. Por ejemplo, podemos usar fórmulas diferentes dependiendo del valor de entrada.
Si cada pieza es una función constante entonces la función definida a trozos se llama función constante a trozos o función escalonada.
Por ejemplo, la siguiente función tiene dos partes o trozos:
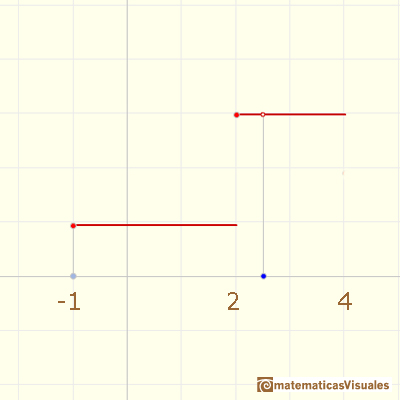
Esta es la notación típica que usamos para esta función:
La gráfica de una función constante a trozos está formada por segmentos horizontales (o quizás, rayos horizontales).
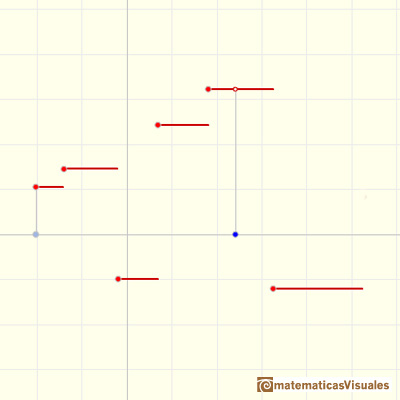
La función 'parte entera' es un ejemplo de función constante definida a trozos que tiene infinitos trozos.
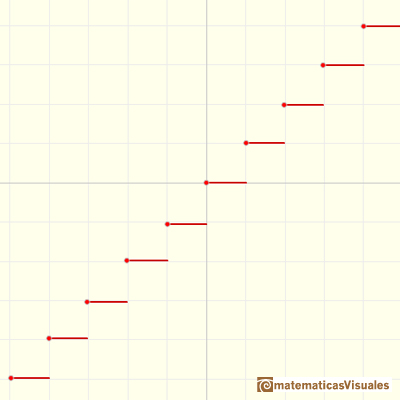
Recordamos que una función definida por f(x)=c, donde c es una constante, es decir un número fijo, se llama función constante. La gráfica de una función constante es una recta horizontal.
Una función constante es un caso particular de una función lineal o afín. La derivada de una función lineal es un ejemplo muy sencillo de derivada, pues es una función constante.
La integral definida de una función constante es el área de un rectángulo (positiva o negativa). Si consideramos la función f como velocidad entonces la integral representa la distancia.
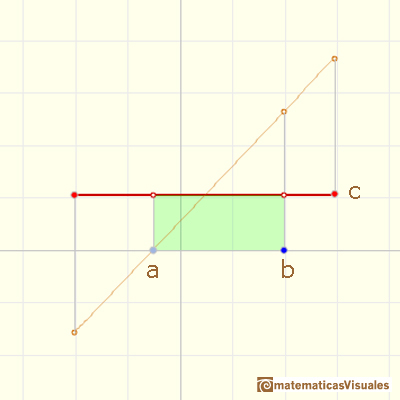
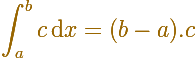
La integral indefinida de una función constante es una función lineal.
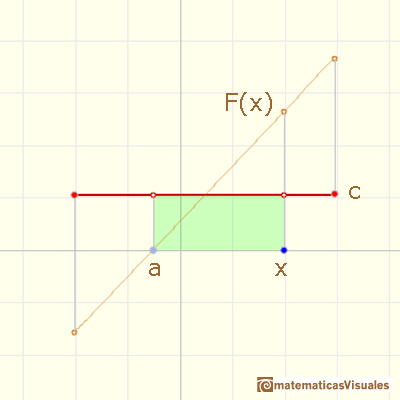
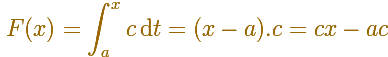

Primitivas de funciones constantes son funciones lineales (es decir, al derivar una función lineal obtenemos una función constante. La derivada de una recta es su pendiente).
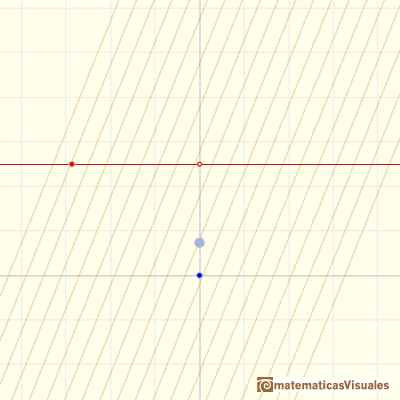
Las pendientes de las funciones lineales son funciones constantes.
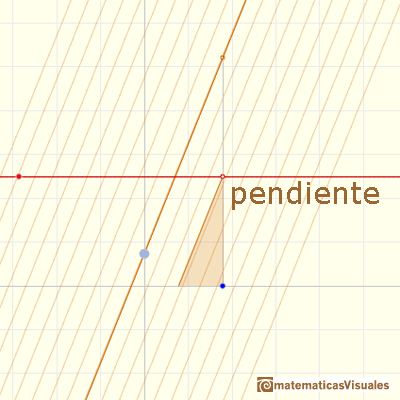
Tom Apostol, en su libro 'Calculus', empieza escribiendo sobre la integral de una función definiendo la integral de una función escalonada.
Para calcular la integral de una función escalonada
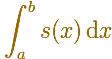
multiplicamos cada valor constante por la longitud de su correspondiente subintervalo.
Entonces el valor de la integral es la suma de las áreas (positivas o negativas) de cada uno de los rectángulos. Notar que este valor es independiente de los valores de la función escalonada en sus puntos de subdivisión. (Apostol, p. 65).
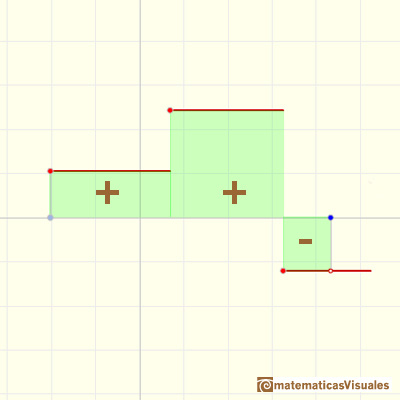
(Después, Apostol prueba varias propiedades importantes de la integral, pags 68-69, y usa esta definición para definir la integral de funciones más generales, aproximando la función por arriba y por abajo por funciones escalonadas. Escribió: "Esta aproximación sigue, de alguna manera, el método de Arquímedes. La idea es sencilla: empezamos aproximando la función f por abajo y por arriba con funciones escalonadas." (p. 72))
Si denotamos la integral indefinida como la función F(x):
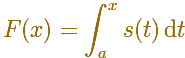
En aquellos intervalos en los que f es constante, la función F es lineal. Decimos que la integral de una función escalonada es lineal a trozos.(Apostol, p. 123)
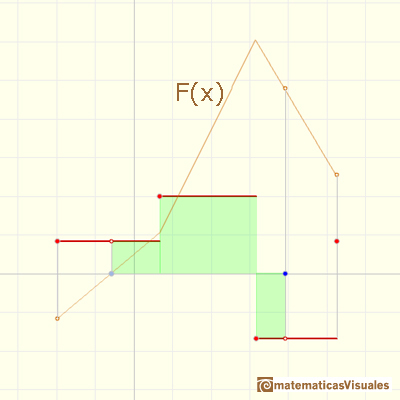
También observamos que la gráfica de f está formada por segmentos desconectados. Hay puntos de la gráfica de f donde un pequeño cambio en x produce un salto en el valor de la función. Notamos, sin embargo, que la integral indefinida correspondiente no tiene ese comportamiento. Un pequeño cambio en x produce solo un pequeño cambio en F(x). Esta es la razón por la que la gráfica de F no esta desconectada. Esto ilustra una propiedad general de la integral indefinida que se conoce como continuidad. (Apostol, p. 124).
También Spivak escribió que parece que F se comporta siempre mejor que f.
Es interesante comprender la relación entre estas funciones, f y F, que van en pareja. F es la integral de f y f es la derivada de F.
Para tener una idea intuitiva de esta relación el uso de gráficos y de pendientes y áreas son un apoyo visual muy poderoso. En la opinión de Gilbert Strang lo mejor es ver f como velocidad y F como distancia. Ambos puntos de vista son complementarios.
Ya conocemos una de estas parejas de funciones: f constante y F lineal. La segunda pareja está solo a un paso y es la que estamos estudiando ahora: una función f que es constante a trozos y una F que es lineal a trozos.
Los siguientes ejemplos son del artículo de Gilbert Strang.
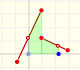
Podemos entender la siguiente gráfica como ir hacia delante y hacia atrás (velocidad constante positiva y negativa):
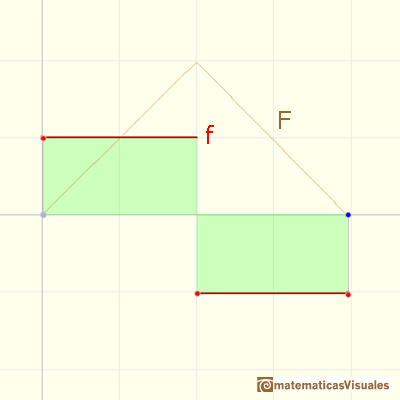
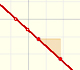
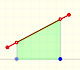
Un incremento constante de velocidad imita f(x) = 2x
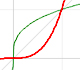
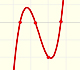
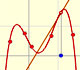
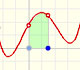
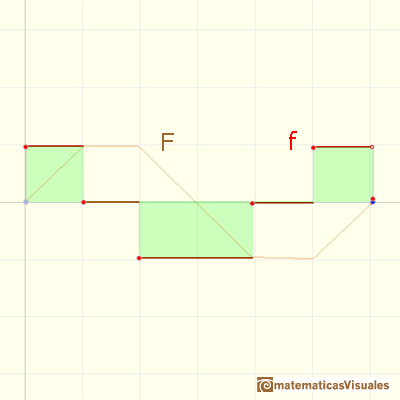
Una velocidad oscilante imita f(x) = cos(x) y F(x) se parece, a grandes rasgos, a una curva seno:
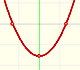
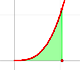
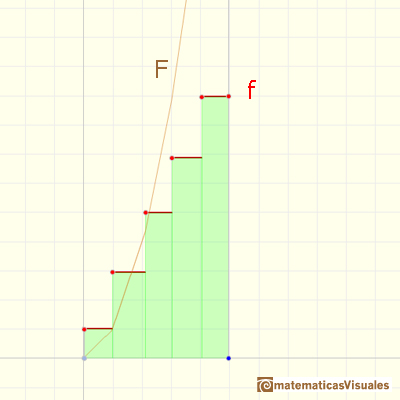
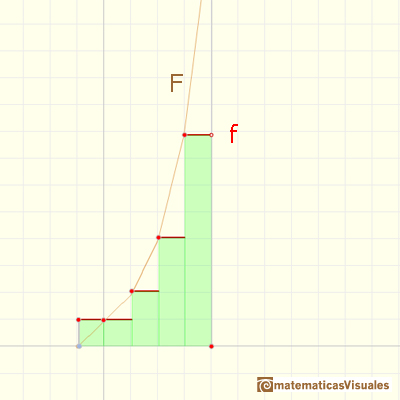
Un incremento exponencial de velocidad imita f(x) = 2^x:
Un arranque brusco de velocidad (y despues parar) hace que F imite a una función escalonada:
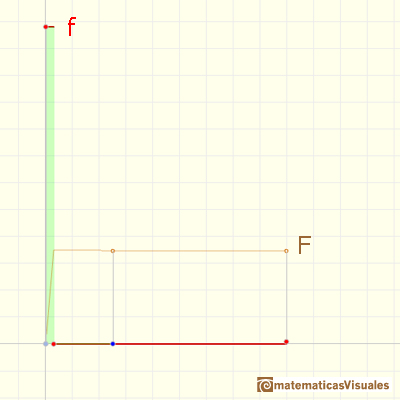
Vemos que si f es una función constante a trozos, F es una función lineal continua a trozos. Pero esta función F no es una función diferenciable. En algunos puntos no es 'suave'. Podemos decir que la integral indefinida de una función escalera es diferenciable a trozos.
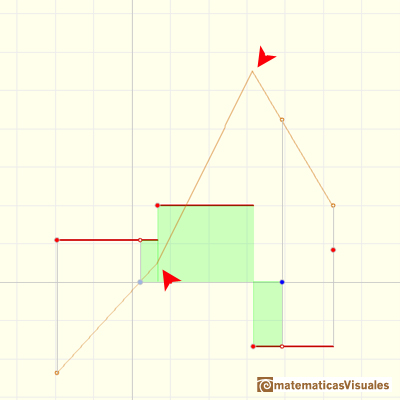
En este caso podemos ver que la función diferenciable a trozos F tiene derivadas laterales pero que no son iguales en algunos puntos:
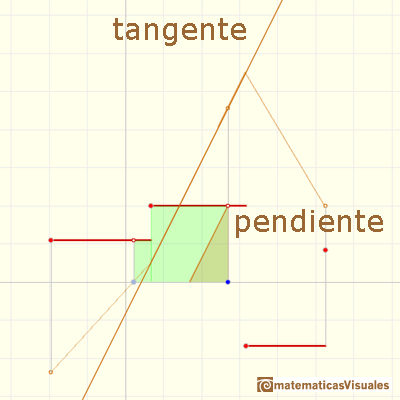
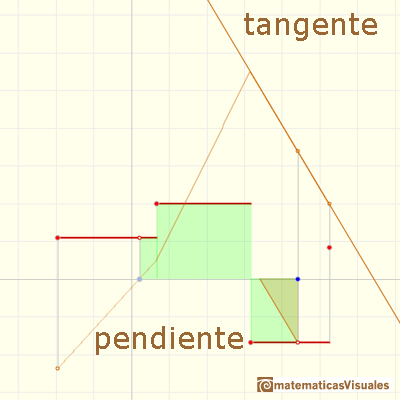
El valor promedio de una función f(x) sobre un intervalo [a,b] es
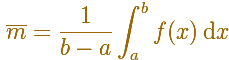
Podemos ver la integral como un área o una distancia. Si consideramos f como una velocidad, el sentido del valor promedio es la velocidad media.
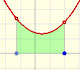
La idea es que el área bajo la función (positiva o negativa) ...
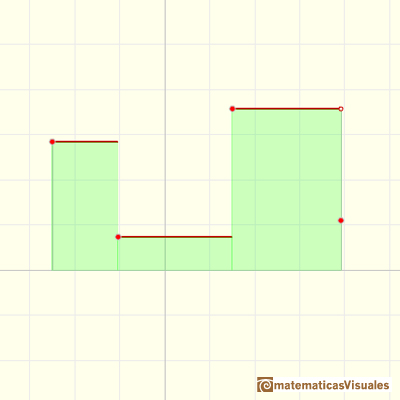
... es igual al área de un rectángulo cuya altura es el valor promedio.
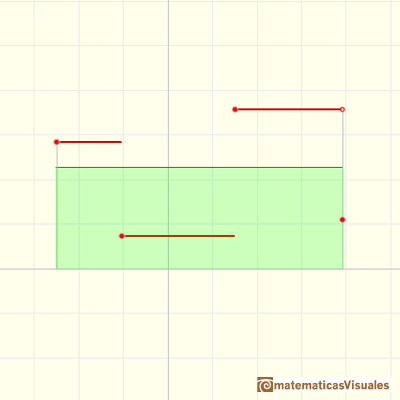
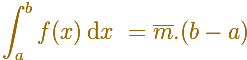
Primer ejemplo (un promedio sencillo):
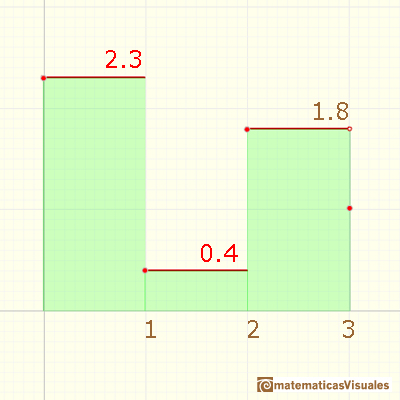
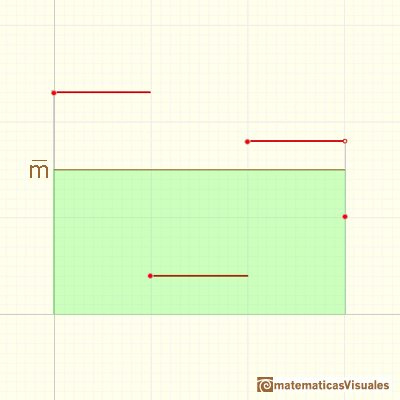
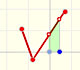
Segundo ejemplo (promedio ponderado):
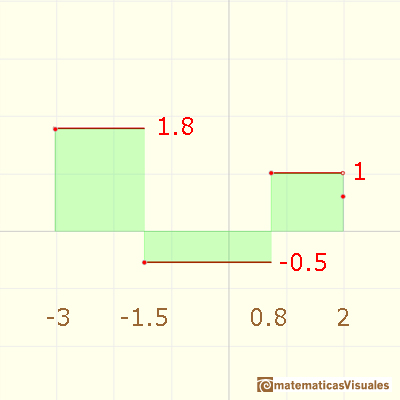
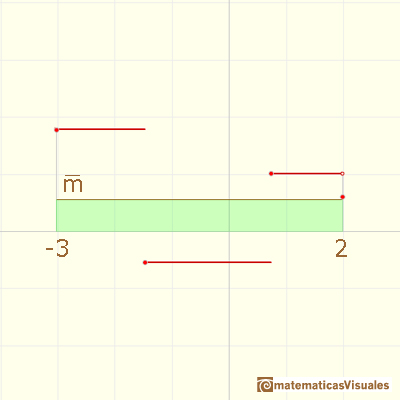
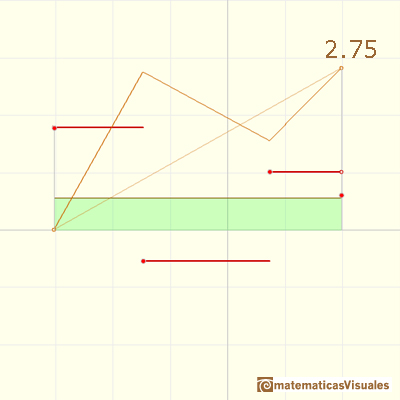
Para continuar podemos estudiar un poco más las funciones continuas lineales a trozos y su relación con las funciones escalonadas y el Teorema Fundamental del Cálculo.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES