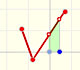
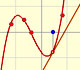
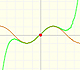
Un tipo muy importante de problemas es cuando conocemos la derivada de una función (la tasa de variación instantánea o la pendiene a su gráfica) y queremos encontrar la función. Por ejemplo, conocemos la velocidad y queremos calcular el espacio recorrido.
El proceso de encontrar una función a partir de su derivada se llama antidiferenciación, también decimos que buscamos una función primitiva o una integral indefinida. La antidiferenciación es una operación inversa a la diferenciación.
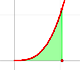
El uso de la palabra integración aquí puede parecer extraño ya que el problema de integración está relacionado de alguna manera con encontrar un área (es un proceso de acumulación, de suma) mientras que la diferenciación está relacionada con la idea de variación instantánea o con la pendiente de la tangente a la gráfica de una función. No parece, en principio, que estos problemas estén relacionados. Sin embargo, veremos más tarde que estos dos problemas están profundamente conectados (Teorema fundamental del Cálculo) y que, de algún modo, integración y diferenciación son procesos inversos.
Se dice que F(x) es una antiderivada (o una primitiva o una integral indefinida) de f(x) en un intervalo abierto si la derivada de F es f para todos los valores de x en el intervalo.
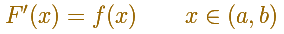
Es interesante notar que definimos 'una' primitiva y no 'la' primitiva. Esto es debido a que las funciones primitivas no son únicas. Sin embargo las primitivas sólo se diferencian en una constant. Es decir:
Dos primitivas F y G de la misma función f difieren solamente en una constante.
Esto es debido a que su diferencia F-G tiene derivada 0 y entonces F-G es una función constante.
A menudo usamos un signo particular (fue Leibniz el primero en usar como signo de integración una 's' alargada con el significado de 'suma'. Usó este signo para representar una primitiva general de f):
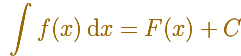
La función f se llama el integrando, la constante C es la constante de integración. El símbolo dx indica que estamos integrando respecto la variable x.
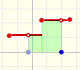
Si conocemos alguna técnica de diferenciación es fácil encontrar primitivas. Por ejemplo, es muy sencillo encontrar la primitiva de una función constante:
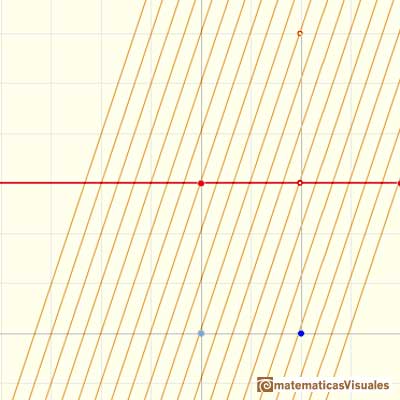
Podemos comprobar en algunos puntos que la derivada es la función constante original:
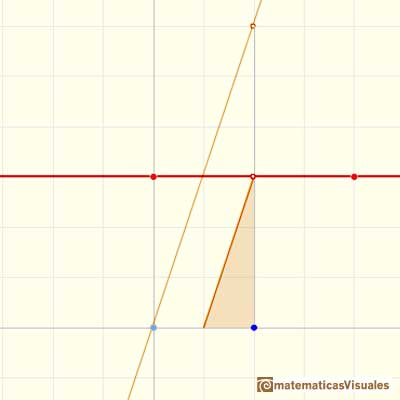
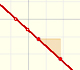
La derivada de un polinomio de grado 1 (una función lineal) es una función constante (de grado 0, una recta horizontal). Entonces, la primitiva de una función constante es una función lineal.
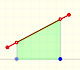
Encontrar primitivas de funciones polinómicas es también sencillo. Por ejemplo, una función lineal básica (la función identidad):
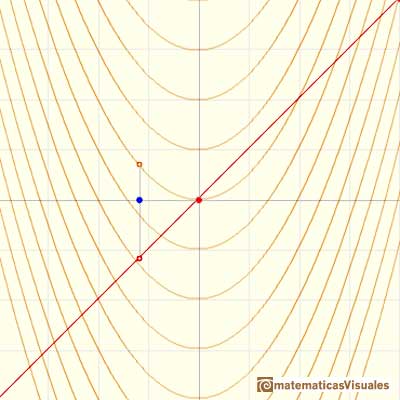
Comprobamos el resultado en un punto:
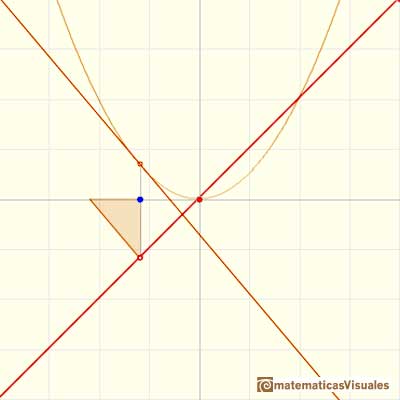
La derivada de un polinomio de grado 2 (una parábola) es un polinomio de grado 1 (una función lineal). Entonces, la primitiva de una función lineal es una parábola.
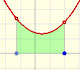
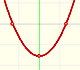
Podemos ver el ejemplo de una función cuadrática (una parábola):
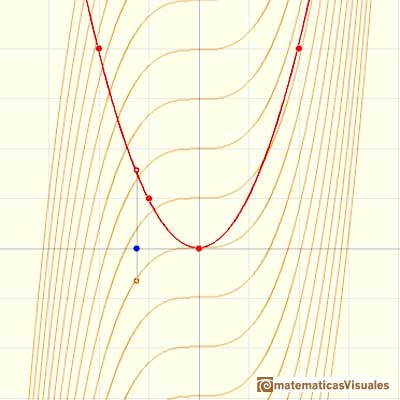
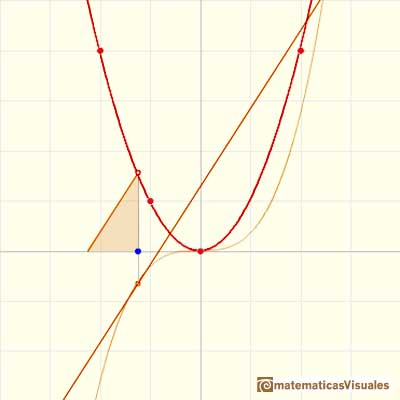
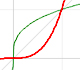
La derivada de una función de grado 3 (una función cubica) es un polinomio de grado 2 (una parábola). Entonces, la primitiva de una parábola es una función cúbica.
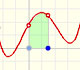
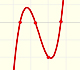
Otro ejemplo, una polinomio de grado 3:
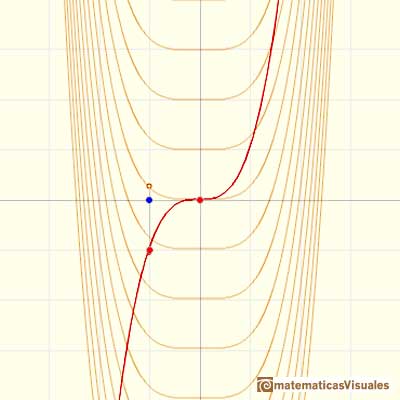
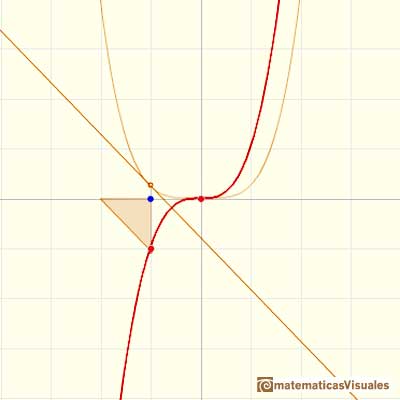
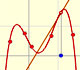
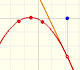
En el siguiente vídeo movemos el punto azul a lo largo del eje X:
Cunado diferenciamos una función polinómica obtenemos una función polinómica de grado uno menor que la función original. Cuando encontramos una primitiva de una función polinómica tenemos una función polinómica de grado uno mayor que la función original.
Encontrar primitivas de funciones polinómicas es sencillo. Sin embargo, encontrar primitivas resulta un problema difícil, en general. El Teorema Fundamental del Cálculo nos dice que siempre podemos construir una antiderivada (o primitiva) de una función continua por integración.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES