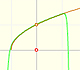
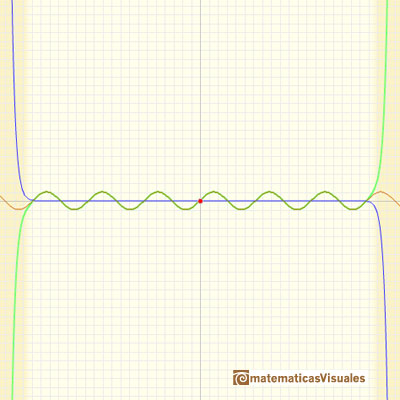
Como en el cso de la función exponencial, las parábolas osculatices
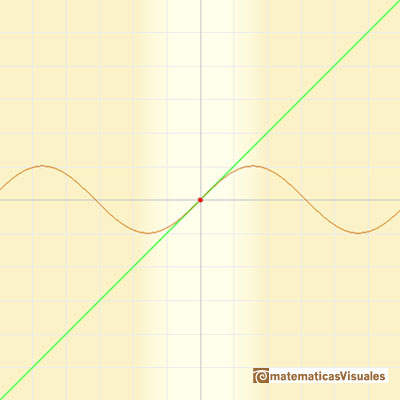
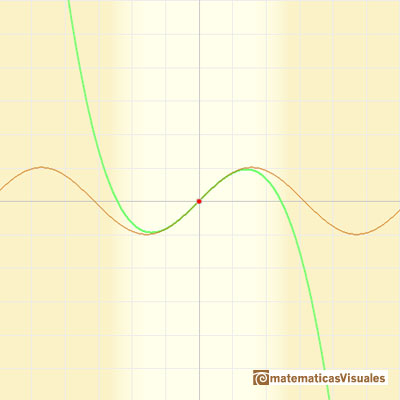
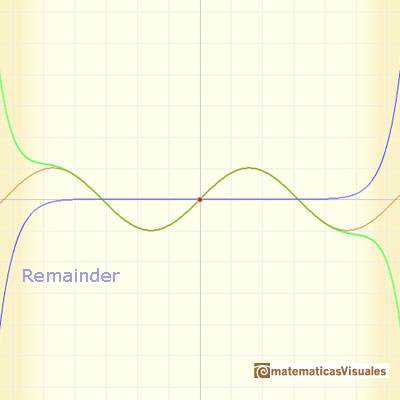
(los polinomios de Taylor de grados cada vez mayores) nos dan aproximaciones en un intervalo cada vez mayor.
Las parábolas hacen el esfuerzo de compartir con la función seno más y más oscilaciones. (Felix Klein)
La serie de Taylor de la función seno en x = 0 es:
Decimos que la función seno es una función impar porque en su serie de potencias (y en los polinomios de Taylor centrados en el origen) los únicos terminos son
los de exponente impar.
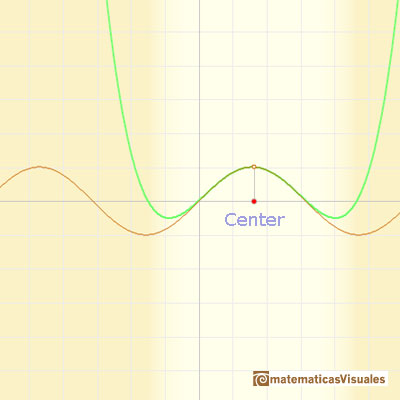
Podemos cambiar el centro del desarrollo de Taylor y ver que el comportamiento de la aproximación es igualmente bueno.
El comportameinto de esta serie de potencias es muy bueno. Decimos que la serie infinita de la función seno converge para todos los
valores de x.
Este no puede ser el caso para todas las funciones. Por ejemplo, ¿qué ocurrirá si algunos valores no pertenecen al dominio de la función?
Podemos estudiar un ejemplo sencillo: Polinomios de Taylor (3): raíz cuadrada.
REFERENCIAS
Felix Klein - Elementary Mathematics from an Advanced Standpoint. Arithmetic, Algebra, Analysis (pags. 223-228) - Dover Publications
MÁS ENLACES

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
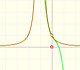
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
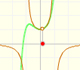
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
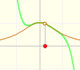
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.
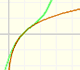
Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

La función coseno compleja transforma rectas horizontales en elipses cofocales.

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
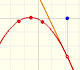
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
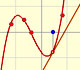
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.

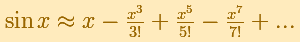
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR