La serie de potencias de la función racional

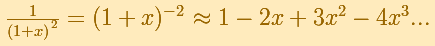
es, al igual que para la raíz cuadrada o esta función racional 1, un caso especial del Teorema del Binomio de Newton. Podemos calcular su serie de Taylor centrada en x = 0 con facilidad.

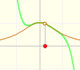
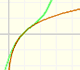
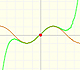
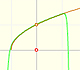
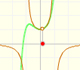
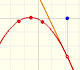
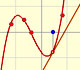
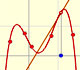
Esta función tiene una singularidad en el punto x = -1. La aproximación es buena entre -1 y +1 pero no fuera de este intervalo. Una vez más encontramos una aproximación adecuada que está centrada en el origen. El círculo de convergencia de la serie es el intervalo (-1,+1)

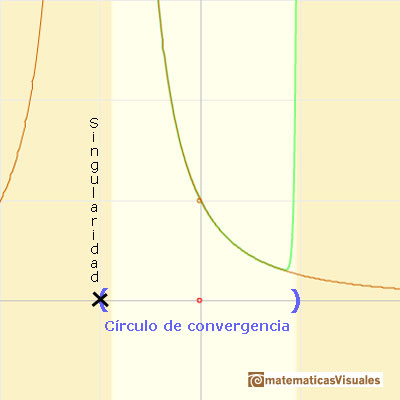
En el punto x = +1 la ordenada crece indefinidamente con el grado, alternando el signo.

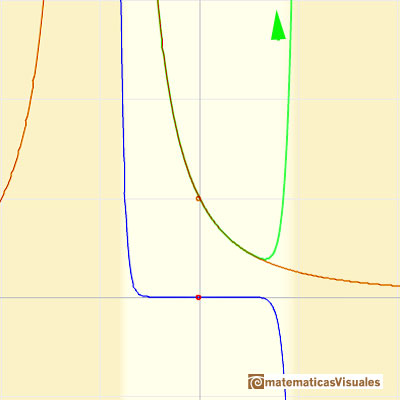
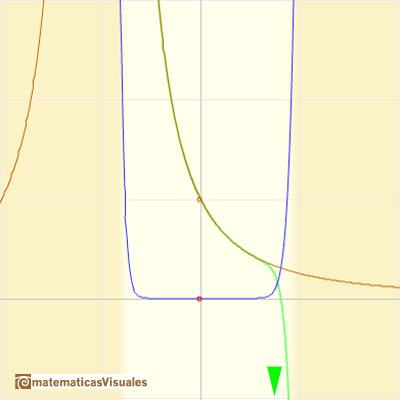
Podemos comparar este comportamiento en la frontera con el de función racional 1.

Klein escribió: "Las consideraciones teóricas de las series de Taylor no pueden completarse sin ir a la variable compleja. Sólamente entonces podemos entender el que la serie de potencias deje repentinamente de converger en lugares donde la función es completamente regular. Para empezar, podemos quedarnos satisfechos, en el caso de nuestros ejemplos, diciendo que la serie no puede converger más allá por la derecha y por la izquierda, y que la convergencia no puede ir más allá debido a la singularidad en x = -1." (Klein, p. 227)

Podemos ver más ejemplos para comprender mejor esta cuestión. Por ejemplo en Polinomios de Taylor (6): función racional con 2 singularidades.

REFERENCIAS

MÁS ENLACES

Polinomios de Taylor (7): función racional sin singularidades reales

La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Mercator y Euler: La función logaritmo

Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

Polinomios de Taylor: función racional compleja con 2 singularidades

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.

Polinomios de Taylor (1): función exponencial

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

Polinomios de Taylor (2): función seno

Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.

Polinomios de Taylor (3): raíz cuadrada

La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Funciones polinómicas y derivada (1): Funciones afines

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

Funciones polinómicas y derivada (2): Funciones cuadráticas

La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

Funciones polinómicas y derivada (3): Funciones cúbicas

La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

Funciones polinómicas y derivada (4): Polinomios de Lagrange (funciones polinómicas en general)

Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.