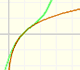
Esta función racional

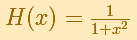
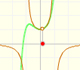
es una función continua. No tiene singularidades (reales). Podríamos esperar que el comportameinto de su serie de potencias fuera semejante al de otras funciones continuas como la función exponencial o la función seno. Es decir, que la serie de potencias convergiera en todos los números reales.

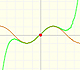
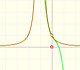
Pero no pasa eso. Aunque la razón no está clara, la serie de Taylor se comporta de un modo semejante al de otras funciones no continuas, por ejemplo, esta función racional con dos singularidades reales. En ese caso, vemos que el radio de convergencia es la distancia desde el centro de la serie de potencias a la singularidad más cercana. Sin embargo, la función que estamos estudiando ahora no tiene ninguna singularidad real, es continua.

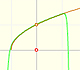
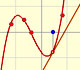
La serie de potencias converge en un intervalo centrado en el centro del desarrollo pero no fuera de él. ¿Cómo está determinado este intervalo y qué explicación tiene?

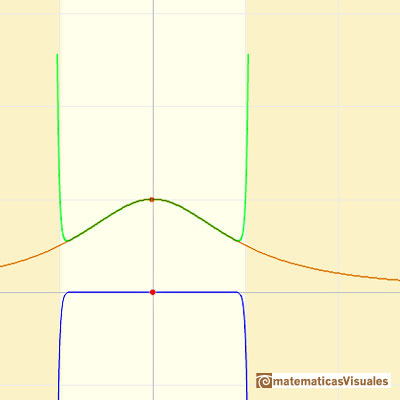
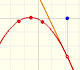
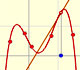
El radio de convergencia, R, parece ser la distancia desde el centro del desarrollo a uno de los puntos fijos que están fuera del eje real, una unidad desde el 0 en dirección perpendicular al eje. Si el pensamos el plano como el plano complejo, estos puntos son +i y -i. Podemos cambiar el centro para ver diferentes casos.

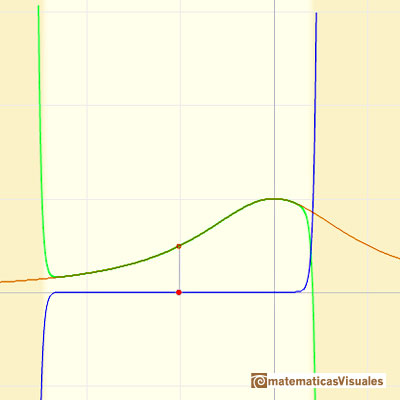
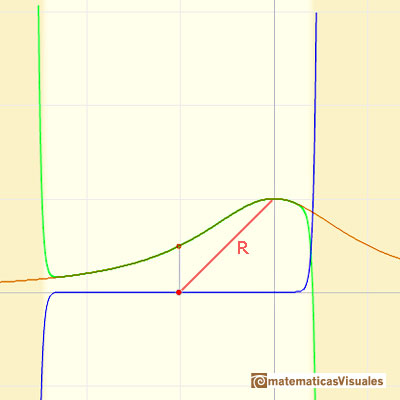
Este comportamiento parece misterioso. Qué impide a la serie converger para todos los valores de x? "El misterior empieza a desvelarse cuando consideramos la función compleja

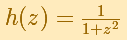
que es idéntica a H(x) cuando z se restringe al eje real en el plano complejo." (Tristan Needham)

Está claro que la función tiene dos singularidades complejas en z = i y en z = -i. La serie de Taylor converge dentro del círculo cuyo radio de convergencia es la distancia del centro a la singularidad más cercana. Es decir, es lo mismo que encontramos en el caso de funciones reales con singularidades reales. En el caso de esta función real eso es lo que ocurre: el radio de convergencia es la distancia desde el centro de la serie al punto i en el plano complejo.

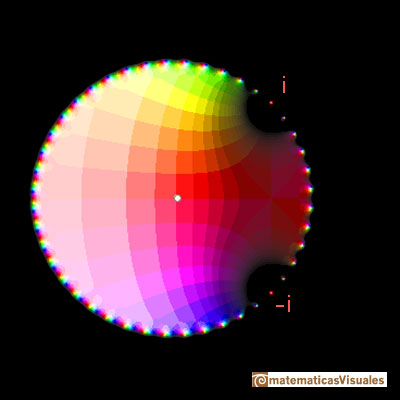
Podemos ver más sobre esta función compleja en Taylor polynomials: Rational function with two complex singularities.

REFERENCIAS

MÁS ENLACES

Mercator y Euler: La función logaritmo

Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

Polinomios de Taylor (1): función exponencial

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

Polinomios de Taylor (2): función seno

Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.

Polinomios de Taylor (3): raíz cuadrada

La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (4): función racional 1

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (5): función racional 2

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor: función exponencial compleja

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

Polinomios de Taylor: función coseno compleja

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Funciones polinómicas y derivada (1): Funciones afines

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

Funciones polinómicas y derivada (2): Funciones cuadráticas

La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

Funciones polinómicas y derivada (3): Funciones cúbicas

La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

Funciones polinómicas y derivada (4): Polinomios de Lagrange (funciones polinómicas en general)

Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.