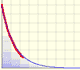
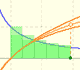
"La Logarithmotechnia de Nicolas Mercator (1620-1687)se publicó en 1668. Las dos primeras partes de este libro estaban
dedicadas al cálculo de una tabla de logaritmos comunes. (...)
Es la tercera parte de la Logarithmotechnia, que es muy diferente, la que tiene ahora mayor interés. Aquí Mercator
encuentra su famosa serie (que parece que ya fue usada por Newton previamente)
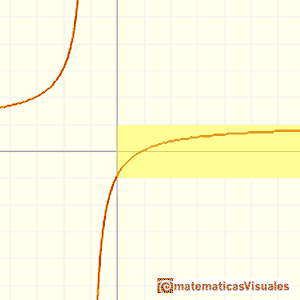
para el área bajo la hipérbola
sobre el intervalo de 0 a x."(Edwards, pág. 162)
Ya se sabía hacia 1660, como consecuencia del trabajo de Gregory St. Vincent y de Sarasa , que hay una
relación entre el área bajo la hipérbola y el logaritmo.
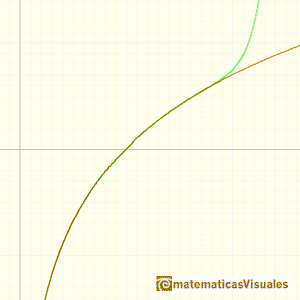
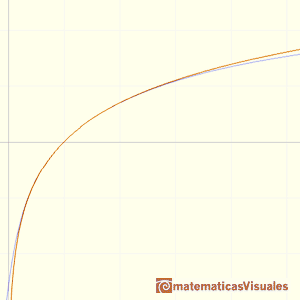
La serie de Mercator para el logaritmo aproxima la función sólo entre 0 y 2. Además, su convergencia es muy lenta
y su uso no es práctico para calcular logaritmos.
Euler sustituye x por -x en la serie de Mercator y resta los logaritmos para obtener
Euler usa una función racional
y su serie converge para todos los números reales.
Además, podemos ver en el mathlet lo rápido que converge esta serie de Euler.
MÁS ENLACES
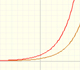
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
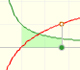
Integrando la hipérbola equilátera podemos definir una nueva función que es el logaritmo natural.
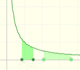
Hemos definido la función logaritmo como una integral de la hipérbola equilátera. Esta integral tiene una importante propiedad que nos permitirá usar los logaritmos para transformar multiplicaciones en sumas.
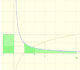
Usando los logaritmos podemos multiplicar dos números haciendo una suma: el logaritmo de un producto es igual a la suma de los logaritmos de los factores.

El número e, la base de los logaritmos naturales, se puede definir como una integral o como el límite de una sucesión relacionada con el interés compuesto. Ambas definiciones coinciden.
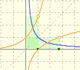
Partiendo de la definición de logaritmo podemos definir la exponencial como su inversa.

Diferentes hipérbolas permiten definir logaritmos y exponenciales (sus inversas).

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

La función exponencial compleja extiende la función exponencial real al plano complejo.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.

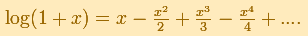
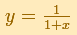
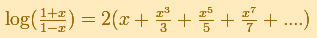
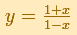
 ANTERIOR
ANTERIOR



















 SIGUIENTE
SIGUIENTE