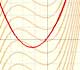
En esta página vamos a estudiar una familia de funciones que se llaman funciones exponenciales. Reciben este nombre pues en sus fórmulas aparece la variable independiente x en el exponente.
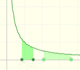
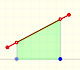
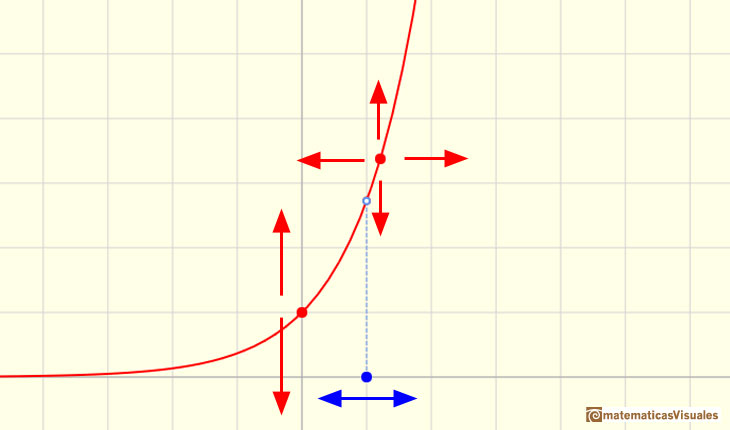
En la aplicación interactiva dos puntos (rojos) determinan una función exponencial. Uno de estos puntos se mueve solo sobre el eje de ordenadas, el eje vertical Y. Marca el punto en el que la gráfica de la función corta al eje vertical. Este valor es importante, en particular por lo sencillo que resulta calcularlo. El otro punto rojo se mueve libremente. La única condición es que ambos puntos no pueden tener la misma coordenada x, es decir, no pueden estar en una recta vertical.
Si movemos ambos puntos la función exponencial tiene la forma general
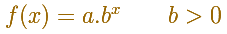
El valor del factor a está determinado por la posición del punto rojo sobre el eje de ordenadas. En un primer momento no vamos a modificar ese valor pues queremos que valga 1.
Entonces la fórmula resulta
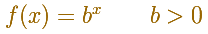
Decimos que b es la BASE de la función exponencial. Notamos que se exige que sea mayor que 0.
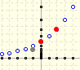
Las funciones exponenciales están directamente relacionadas con las progresiones geométricas. Podemos decir que las progresiones geométricas de razón positiva son funciones exponenciales pero con su dominio restringido a los Números Naturales.
INVESTIGA
Relaciona los conceptos de 'termino inicial' y 'razón' de una progresión geométrica con el factor a y la base b de una función exponencial.
Cuando la razón de una progresión es negativa la progresión oscila entre valores positivos y negativos. Para las funciones exponenciales no queremsos ese comportamiento oscilante. Entonces se exige que la base de una función exponencial sea positiva.
Las funciones exponenciales son importantes por muchos motivos. Estan relacionadas con un crecimiento (o decremiento) exponencial. En estas situaciones la variable independiente x se suele considerar el tiempo. Entonces hablamos de crecimiento (o decrececimiento) exponencial cuando la función varía en el tiempo proporcionalmente a su valor.
Hay muchas situaciones, en contextos muy distintos, en los que encontramos fenómenos que crecen exponencialmente. Por ejemplo, el crecimiento de una colonia de bacterias, la historia del inventor del tablero de ajedrez, doblando una hoja de papel repetidas veces, la difusión de los rumores y de los mensajes de correo del tipo 'envía este mensaje a 10 personas para ....', las estafas piramidales, reacciones nucleares en cadena, la desintegración radioactiva, el interés compuesto, cuando se habla de crecimiento económico continuo del tanto por ciento, los crecimientos orgánicos en general, etc...
Algunos de estos crecimientos son discretos y, por lo tanto, se pueden modelar con progresiones geométricas. Cuando son continuos es cuando usamos las funciones exponenciales. Estas también se usan para aproximar situaciones discretas.
El crecimiento exponencial no puede ser indefinido pues, como veremos, al cabo del tiempo se hace muy rápido. Por ejemplo, una población no puede crecer exponencialmente siempre pues le faltaría espacio y recursos para sobrevivir.
INVESTIGA
Busca información sobre alguna situación cuyo modelo sea un crecimiento exponencial y analiza los límites de ese crecimiento en el mundo real.
Esta información se puede encontrar en muchos sitios pero un libro antiguo y muy clarificador es 'Matemáticas recreativas' de Yakov Perelman. No es dificil encontrarlo por internet y allí se pueden leer varias historias sobre 'números gigantes'.
No es raro que se presenten las funciones exponenciales de un modo que podemos calificar como de inocente. Partimos de una progresión geométrica y lo que queremos es extender esa progresión a una función que tenga como dominio todos los Números Reales.
La tarea no parece difícil. Sin embargo tiene sus dificultades y por eso cuando queremos hacer una presentación elemental de las funciones exponenciales no hay más remedio que soslayar estas dificultades.
Vamos a exponerlas brevemente con un ejemplo sencillo:
Podemos pensar que es fácil entender el significado de una función como 2x
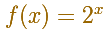
(o 3x o 10x) porque podemos calcular
Pero ¿cuál es el significado de la siguiente potencia?
No hay una manera sencilla de definir 2x para exponentes x irracionales. Cuando se estudia con un poco más de profundidad este asunto se suele usar los 'desarrollos en serie de potencias' y también es habitual definir previamente las 'funciones logaritmo'. Podemos ver la relación entre las funciones exponenciales y logarítmicas en otras páginas de matemáticasVisuales.
Vamos a ver algunas propiedades de las funciones exponenciales.
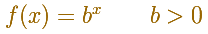
Esperamos que esta función cumpla la ecuación fundamental
También
Cuando el factor a es 1 todas las funciones exponenciales pasan por el punto (0,1).
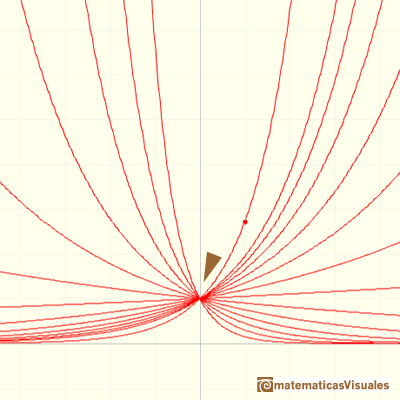
Algunas de estas funciones son crecientes (cuando b > 1)
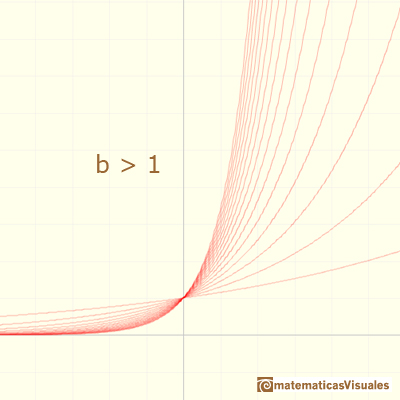
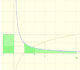
Algunas son decrecientes (cuando b < 1)
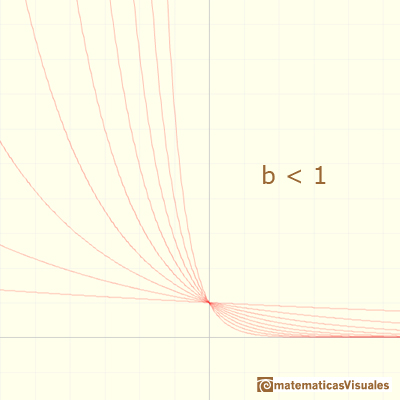
INVESTIGA
Modifica el punto rojo que controla la base de la función y comprueba la relación entre el crecimiento o decrecimiento de la función y el valor de la base.
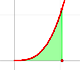
Observa que incluso cuando la base es solo un poco mayor que 1 el crecimiento de la función se hace muy grande conforme consideramos valores de x grandes aunque para valores 'pequeños' ese crecimiento sea 'pequeño'. Esta es una característica fundamental de las funciones exponenciales.
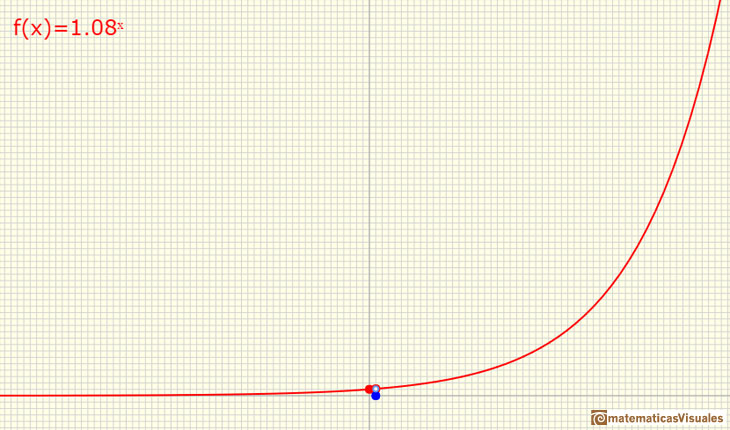
Las funciones exponenciales se caracterizan porque todas tienen una forma parecida pero que se diferencian por la base.
De entre estas funciones hay una que destaca por sus propiedades. Es la que tiene como base un número especial (que al principio nos puede parecer un poco extraño) que llamamos número e (esta notación se debe a Euler).
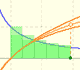
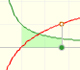
El número e se puede definir de varias maneras. Nosotros nos vamos a fijar, para empezar, en la pendiente de la tangente a diferentes funciones exponenciales en x=0.
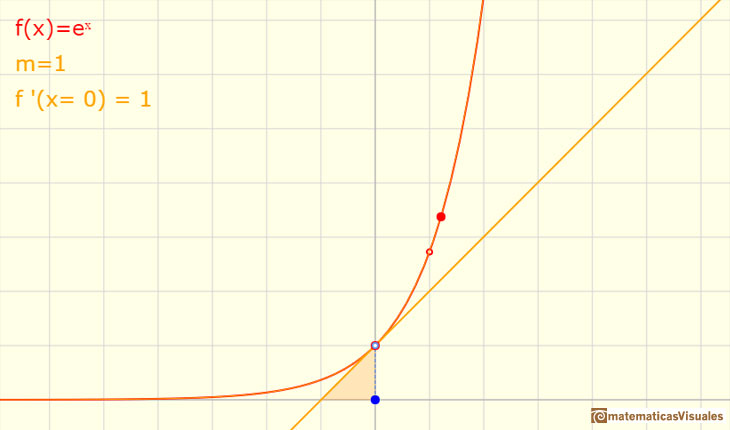
Si miramos la tangente a este tipo de funciones en x=0 podemos ver que hay una base para la que la pendiente de la tangente de la función en x=0 es 1. Llamaremos a ese número e.
INVESTIGA
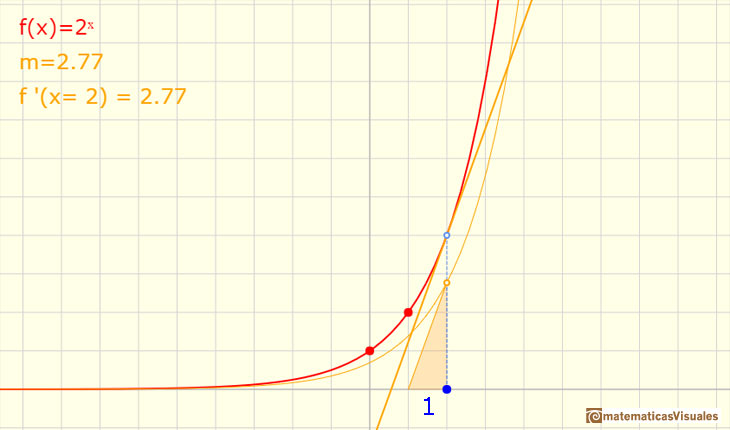
Marca la casilla 'Tangen.' y coloca en punto azul en x=0. Modifica la función exponencial hasta que la pendiente sea m=1. Observa que el número e es un poco mayor que 2,7.
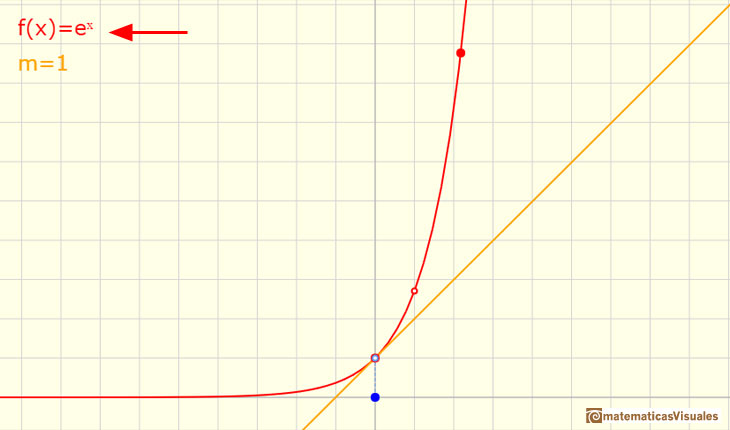
Siguiendo a Serge Lang: "La existencia de un número e que tiene la propiedad comentada arriba puede motivarse de la siguiente manera. Sean a, b números > 1 y supongamos que a < b. Entonces, para todos los números x se cumple
Si b es muy grande, entonces la curva y=bx tendrá una pendiente muy grande en x=0, mientras que si b es solo un poco mayor que 1 la pendiente será muy pequeña.
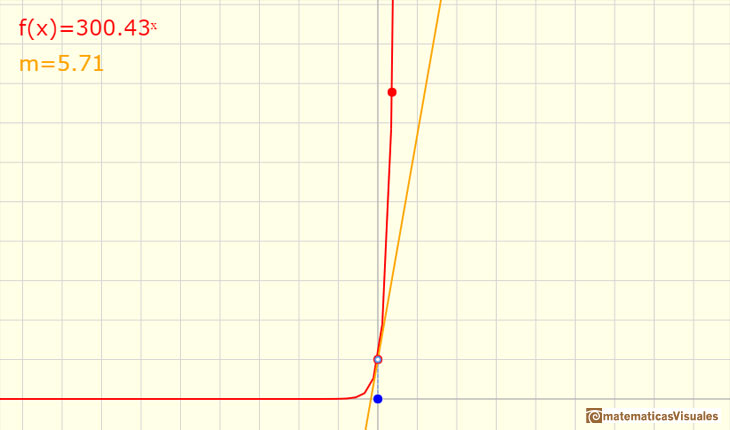
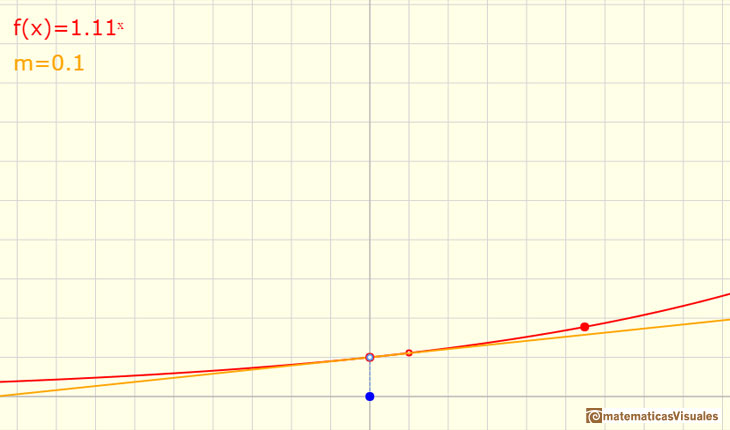
Es razonable pensar que conforme la base crece desde números cercanos a 1 (y mayores que 1) a números muy grandes, la pendiente de bx en x=0 crece continuamente desde valores cercanos a 0 a valores muy grandes y, entonces, para algún valor de b, que llamamos e, esta pendiente será precisamente 1. Desde este punto de vista intuitivo, e es el número tal que la pendiente de ex en x=0 es igual a 1." (Serge Lang)
Más adelante veremos cómo se puede calcular aproximadamente e. Su valor es
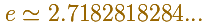
Realmente para dibujar las rectas tangentes usamos una herramienta fundamental que es la derivada. Vamos a avanzar en esa dirección planteándonos primero un límite pues la derivada de una función en un punto se puede definir como la pendiente de la tangente a la gráfica en ese punto y la pendiente de la tangente es el límite de las pendientes de rectas rectantes pasando por ese punto. Lo que estamos haciendo aquí es tratar un caso particular de esa definición.
Usando límites, la pendiente de la tangente en x=0 es (si el límite existe)
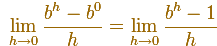
Notamos que este límite, si existe, solo depende de b.
Lo que decimos es que existe un número e tal que
Si pensamos un poco más en la definición de derivada de una función para una función exponencial, si el límite existe y usamos la propiedad de las exponenciales, podemos escribir
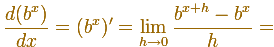
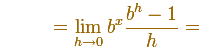
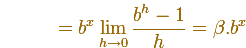
Es decir, la derivada de una función exponencial es un múltiplo de la función (aunque todavía no conocemos el valor de ese factor). En particular, la derivada de una función exponencial es otra función exponencial.
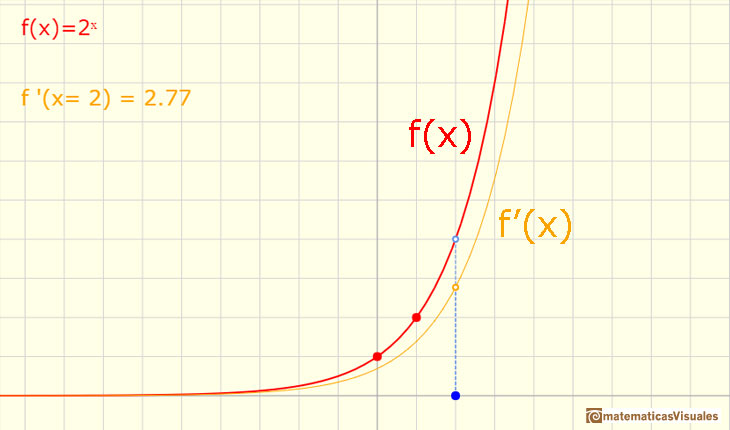
INVESTIGA
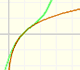
Marca la casilla 'Deriv.' y considera funciones exponenciales con bases mayores y menores que 1. Observa cómo cambian las funciones derivadas. Unas veces la derivada es siempre positiva y otras siempre negativa. Relaciona este hecho con las pendientes de las tangentes en diferentes puntos y con el crecimiento y decrecimiento de la función.
Para un caso particular, la derivada de una función exponencial coincide con la misma función. Esto ocurre cuando b = e pues encontes el límite que hemos estudiado vale 1. Esta es la función exponencial por excelencia pues cumple esta propiedad tan importante:
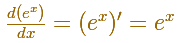
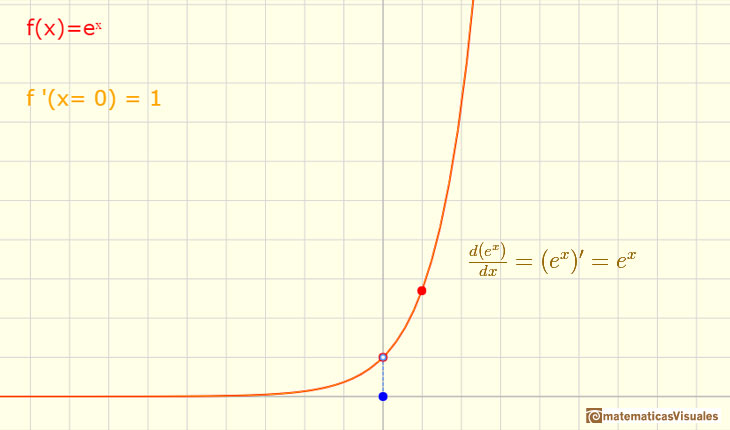
INVESTIGA
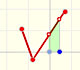
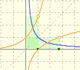
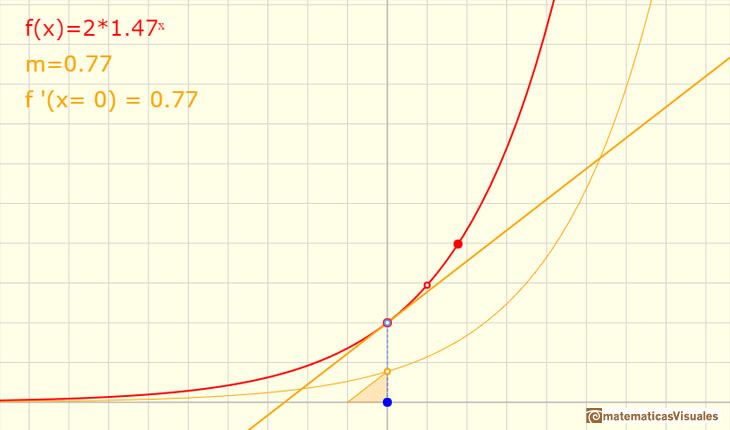
Observa en la aplicación interactiva la relación que hay entre la derivada de una función en un punto y la recta tangente. Observa el triángulo que se dibuja y cómo su hipotenusa es paralela a la tangente.
Mira lo que ocurre cuando la base es e.
Hasta ahora no hemos movido el punto rojo que se desplaza por el eje de ordenadas. Si modificamos ese punto estamos cambiando el valor de f(0), es decir, el punto por el que la gráfica de la función corta al eje vertical.
La función exponencial que estamos considerando ahora es un poco más general:
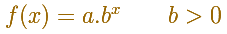
En realidad se trata de múltiplos de funciones exponenciales. Ese múltiplo podría ser positivo o negativo aunque en la aplicación solo se permiten valores positivos.
INVESTIGA
Explora diferentes funciones exponenciales generales y sus derivadas.
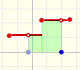
Dos puntos que no estén en la misma recta vertical determinan una función exponencial. Si los dos puntos están en una recta horizontal la función exponencial es una recta (su base entonces es 1). Esta recta (y el valor b=1) separa las funciones exponenciales crecientes de las decrecientes.
Si conoces las propiedades de los logartimos ¿podrías calcular la función exponencial que pasa por dos puntos dados? Así es como se ha programado la aplicación interactiva.
En esta página hemos practicado con funciones exponenciales pero seguimos teniendo el problema con la definición de este tipo de funciones. No conocemos todavía el significado de
Una idea es introducir los logaritmos primero y usar los logaritmos para definir las funciones exponenciales.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES