Progresiones geométricas o sucesiones geométricas
Una sucesión es una lista ordenada de números. Algunas sucesiones siguen una regla, otras no.
Cada número de una sucesión se llama un término.
Podemos ver las sucesiones como funciones. El dominio son los números naturales.
Una sucesión geométrica (o progresión geométrica) es una sucesión en la que los términos después del primero se obtienen multiplicando el término anterior por un número fijo distinto de cero, una constante, que se llama razón.
La palabra razón proviene de la Matemática griega y, en este contexto, significa división o cociente. La razón de una sucesión geométrica se obtiene dividiendo un término entre su anterior. Siempre se obtiene la misma constante.
Los términos de una sucesión geométrica pueden expresarse por medio de una fórmula del término general:

Cuando la razón r es mayor que 1 obtenemos una secuencia creciente (crecimiento exponencial).
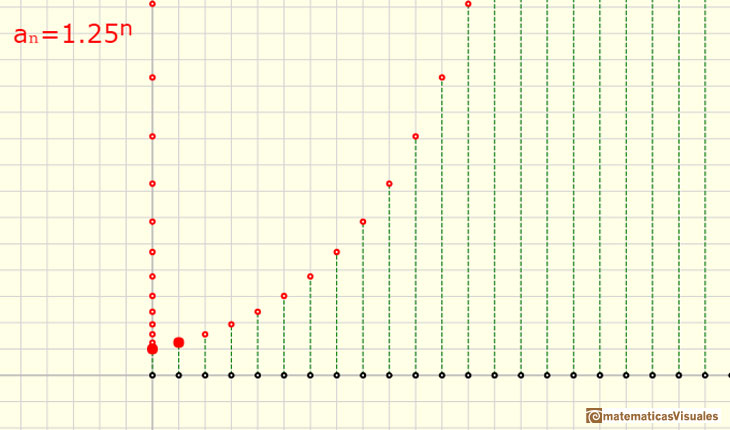
El crecimiento exponencial empieza generalmente poco a poco, lentamente, pero después de un número suficiente de pasos el crecimiento se hace cada vez mayor. Incluso cuando la razón es sólo un poco mayor que uno. Por ejemplo, éste es el resultado después de 300 pasos con una razón de 1.01.
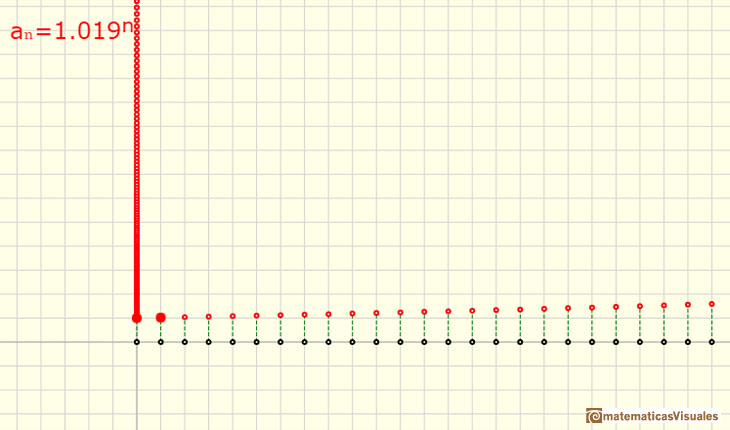
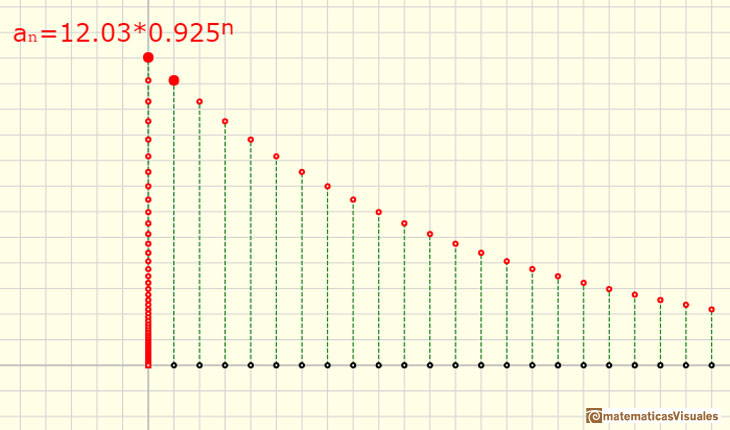
Si la razón r es positiva y menor que 1 la sucesión es decreciente y el término general tiende a 0.
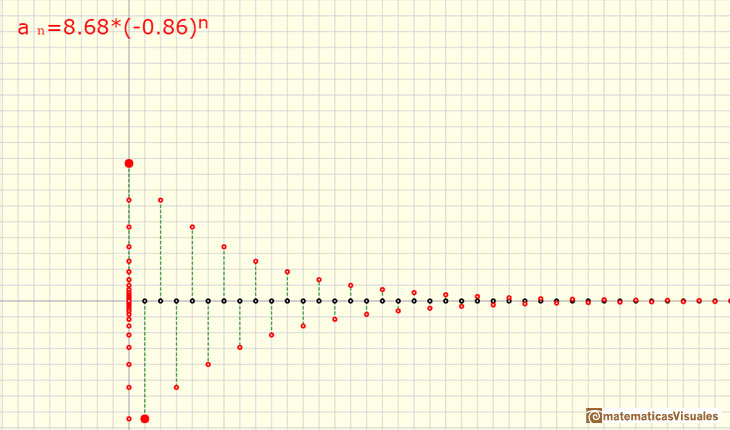
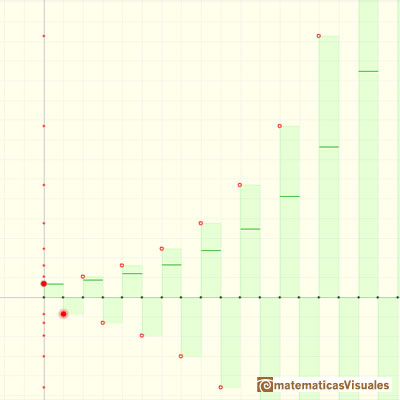
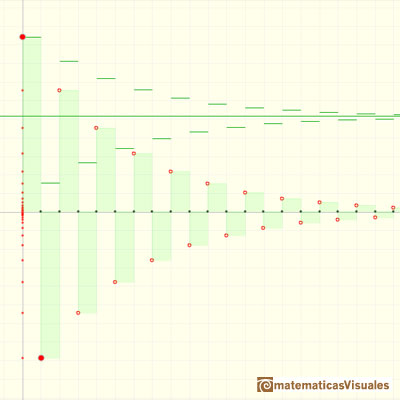
Cuando la razón r es negativa la sucesión se dice alternante. Los signos de los sucesivos términos van cambiando.
Si la razón r está entre -1 y 0 el término general de la sucesión alternante tiende a 0.
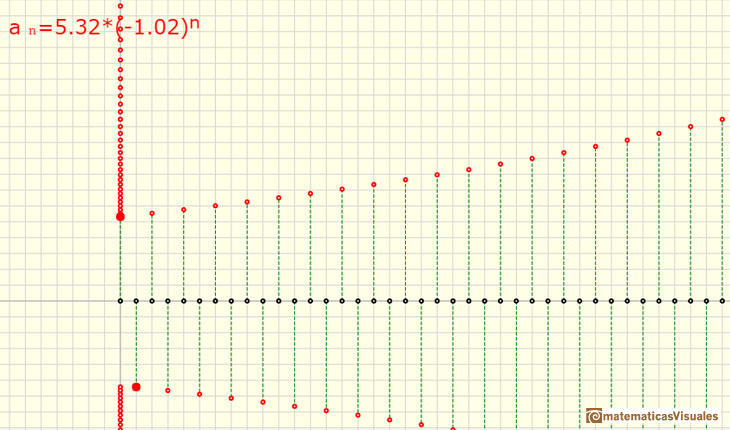
Si la razón r es menor que -1 la sucesión alternante se hace cada vez mayor en valor absoluto. Pero los signos se van alternando.
INVESTIGA
Las progresiones geométricas con razón r positiva están relacionadas con las funciones exponenciales. Las progresiones geométricas pueden verse como funciones cuyo dominio son los Números Naturales. Las funciones exponenciales pueden entenderse como extensiones de las progresiones geométricas a todos los Números Reales.
Estudia esta relación. Puedes hacerlo siguiendo este enlace:
Vamos a estudiar la suma de términos de una progresión geométrica.
Podemos considerar la suma de los primeros términos de una sucesión geométrica. Esto no supone ningún problema especial pues estamos sumando unos pocos números y obtendremos un resultado.
Además resulta que podemos encontrar una fórmula elegante para calcular la suma de términos de una progresión geométrica:
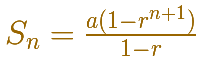
INVESTIGA
Busca información de cómo se obtiene la fórmula anterior. El procedimiento es muy interesante.
Además este procedimiento nos ayudará a comprender la fórmula de la suma los infinitos términos de una progresión geométrica que veremos más adelante.
En la siguiente aplicación podemos jugar con diferentes casos con la razón positiva:
Podemos ver el comportamiento cuando la razón es mayor que 1. En este caso la suma crece y crece:
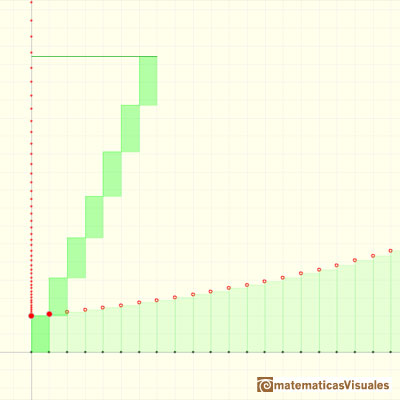
Si sumamos los primeros términos de una sucesión geométrica con razón positiva y menos que 1 el resultado parece que se va aproximando a un número:
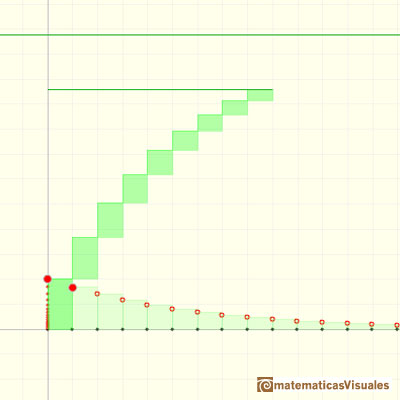
Si nos planteamos sumar los infinitos términos de una sucesión entonces el asunto ya no es tan trivial.
Una serie es la suma de los infinitos términos de una sucesión.
Si la razón r es positiva y menor que 1 podremos sumar los infinitos términos de una sucesión geométrica y obtendremos un número. Decimos que la serie es convergente, que se aproxima a un límite.
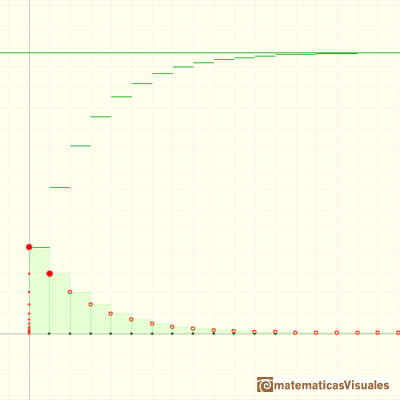
Si la razón r es positiva y mayor que 1 la serie no se aproxima a ningún número. Cada vez se hace mayor y mayor. Crece por encima de cualquier cota que pongamos. Decimos que la serie es divergente.
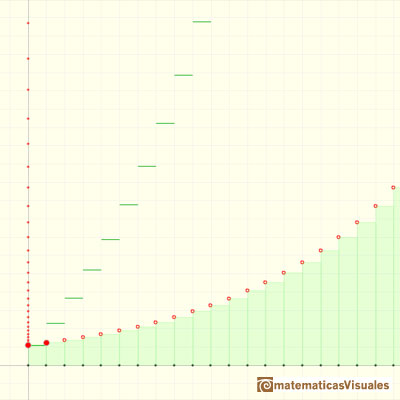
En la siguiente aplicación podemos jugar con el caso general. La razón puede ser positiva o negativa:
Una serie divergente y alternante:
Una serie convergente y alternante:
La condición necesaria y suficiente para la convergencia de una serie geométrica con razón r distinta de cero es:
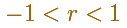
La fórmula para calcular la suma de una serie geométrica convergente es:
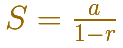
 SIGUIENTE
SIGUIENTE
MÁS ENLACES

La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
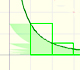
A partir de una función positiva decreciente podemos definir series y aplicar el test de la integral. El test de la integral es un criterio que nos puede ayudar a decidir si una serie converge o diverge. Además, si la serie converge nos dará cotas.
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
Geométricamente, la multiplicación por un complejo es una transformación del plano que consiste en una rotación y una expansión o contracción (rotación dilatativa).