El concepto de integral está asociado al concepto de área. Cuando una figura plana está acotada por líneas rectas es sencillo calcular su área. Sin embargo, áreas acotadas por curvas son más difíciles de calcular (incluso, de definir).
Uno de los momentos clave de la Historia de las Matemáticas fue cuando Arquímedes fue capaz de calcular el área de segmentos de una parábola usando el método de exahución de Eudoxo.
Cavalieri (alrededor de 1630) sabía como integrar funciones potencia (f(x)= x^n) desde n=1 hasta n=9. El resultado general, para n arbitrario, fue obtenido por Fermat.
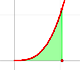
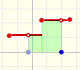
Aunque Cavalieri no conocía el término 'función' podemos decir que una de sus contribuciones fue que él consideró el problema de calcular el área limitada por la gráfica de una función positiva, el eje X y dos rectas verticales (un 'trapezoide curvilíneo' o 'el área bajo una curva')
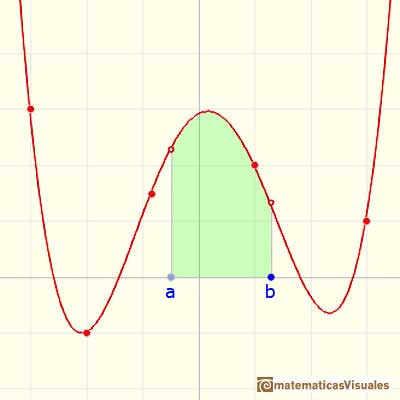
Queremos asignar un número a esta región que represente su área cuando la función sea positiva. Llamaremos a ese número la integral definida de f entre a y b.
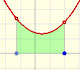
La integral no siempre representa el área de un 'trapezoide curvilíneo'. Ése es el el caso si la función es no negativa. Cuando f es negativa la integral va a ser menos el área. En general, la integral es el área del trapecio curvilíneo que está por encima del eje X menos el área de las partes que están bajo el eje X.
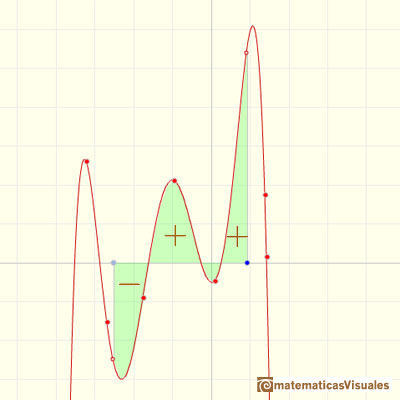
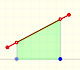
Si queremos integrar funciones lineales el problema es simple.
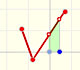
El problema es más difícil cuando la gráfica de la función no es una recta.
"Vamos a seguir una idea de Arquímedes. Es aproximar la función f por funciones horizontales (constantes), y el área bajo f por la suma de rectangulos pequeños." (Lang)
En estos casos queremos construir la integral definida (un número) como el resultado de algún tipo de proceso de límite. Podemos empezar dividiendo [a,b] en subintervalos y tomar la suma de las áreas de ciertos rectángulos que aproximan la función f en varios puntos del intervalo. El área de estos rectángulos aproxima la integral. La integración es un proceso de suma.
Usamos esta notación:
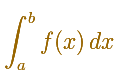
El símbolo S (una S alargada, por suma) se llama signo de integral y fue introducido por Leibniz en 1675. El proceso que produce el resultado se llama integración. Los números a y b, que se ponen junto al signo de integral, se llaman límite de integración inferior y superior.
Leibniz usó este símbolo porque consideraba la integral como la suma de infinitos rectángulos con altura f(x) y cuyas bases eran "infinítamente pequeñas". Fue aceptado rápidamente por muchos matemáticos porque les gustaba pensar que la integración era un tipo de "proceso de suma" que les permitía sumar infinitas cantidades "infinitesimales" (infinitamente pequeñas).
Vamos a ver algunas ideas que están en la definición rigurosa de integral dada por Bernhard Riemann (1826-1866).
P es una partición de [a,b].
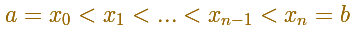
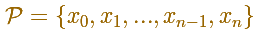
Una partición define unos subintervalos. La longitud de esos subintervalos puede ser diferente:
Dada una partición de [a,b] podemos añadir mas números a la partición y obtenemos una nueva partición que tiene subintervalos más pequeños. Si añadimos suficientes números intermedios entonces los intervalos se pueden hacer arbitrariamente pequeños.
A veces se consideran subdivisiones regulares del intervalo. En este caso, las bases de los rectángulos son iguales:
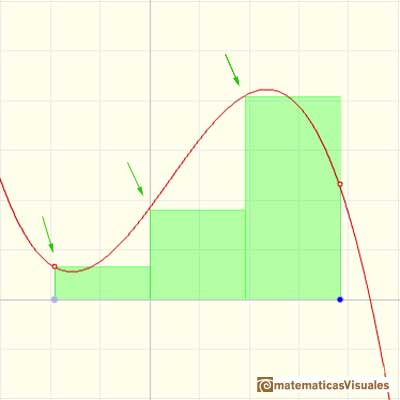
Para cada i tomamos un punto xi* en [xi, xi+1]. El valor f(xi*) puede verse como la altura de un rectángulo.
"La idea principal que vamos a desarrollar es que si hacemos los intervalos de nuestra partición más y más pequeños, la suma de las áreas de los rectángulos se aproximarán a un límite, y podemos usar ese límite para definir el área bajo la curva." (Lang)
Podemos tomar xi* como el punto medio del subintervalo (como en el mathlet y en los ejemplos previos).
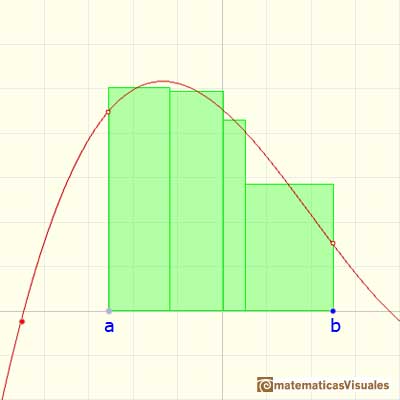
Una elección popular es que xi* se igual a xi, el extremo izquierdo de cada subintervalo. Entonces la altura del rectángulo será f(xi):
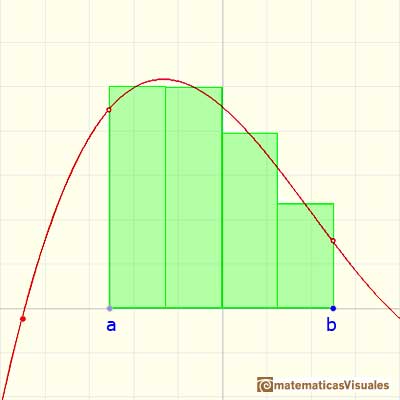
O también podemos tomar xi* igual a xi+1, el extremo derecho del intervalo. Entonces la altura del rectángulo será f(xi+1):
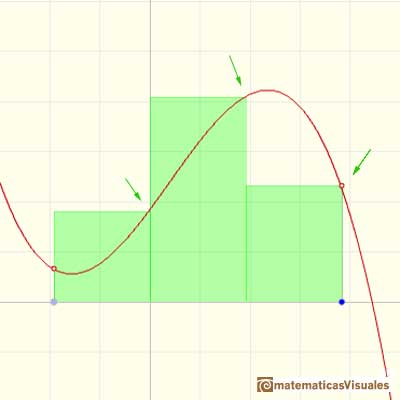
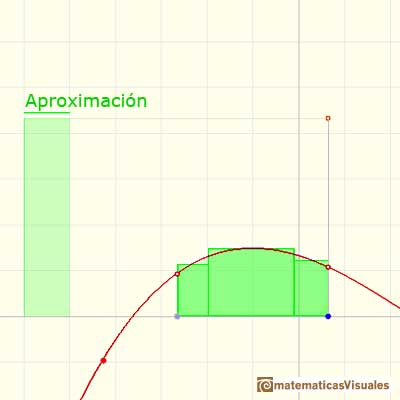
La elección de estos xi* en [xi, xi+1] es arbitraria. Riemann consideró
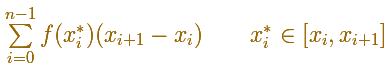
A estas sumas se les llama sumas de Riemann de F para la partición P.
Interpretación geométrica: "Es el área total de los n rectángulos que están en parte por encima de la gráfica de f y en parte por debajo de ella. Debido al modo arbitrario de elección de las alturas de los rectángulos no podemos estar seguros de si una suma de Riemann en particular es menor o mayor que la integral. Pero parece que esta diferencia no debe importarnos demasiado. Si las bases de todos los rectángulos son suficientemente estrechas entonces las sumas de Riemann tienen que aproximarse a la integral." (Spivak)
Si aumentamos el número de rectángulos nos acercaremos (intuitivamente) al valor de la integral definida.
Podemos decir que la integral definida es el límite de las sumas de Riemann cuando el número de subdivisiones tiende a infinito y la longitud de cada subintervalo tiende a cero. Y no importa el punto xi* que tomamos de cada subintervalo.
"La moraleja de esta historia es que algo que parece una buena aproximación a la integral realmente lo es, siempre que las longitudes de los subintervalos de la partición sean suficientemente pequeños." (Spivak)
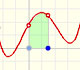
En el mathlet podemos modificar la función y el número de rectángulos. En general, en cada subintervalo, la altura del rectángulo puede ser cualquier valor de la función en un punto del subintervalo, aquí sólo consideramos una posibilidad sencilla: xi* es el punto medio del subintervalo.
"Las integrales de muchas funciones no se pueden determinar exactamente (aunque pueden calcularse con el grado de precisión que se desee calculando sumas de Riemann). Sin embargo, [como veremos más adelante, por ejemplo, cuando estudiemos el Teorema Fundamental del Cálculo], la integral de muchas funciones puede calcularse con facilidad." (Spivak)
Una aproximación axiomática de la integral (siguiendo a Serge Lang)
En su libro 'A First Course in Calculus', antes de explicar las sumas de Riemann, Lang destaca la importancia de dos propiedades que definirán una integral de f on [a,b]:
Sea a, b dos númmeros, con a < b. Sea f una función continua en el intervalo [a,b]. Supongamos que para cada par de números c<=d en el intervalo podemos asociar un número denotado por
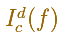
que cumple las siguientes propiedades:
Propiedad 1. Si M, n son dos números tales que
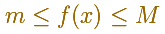
para cada x en el intervalo [c,d]. Entonces
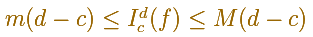
Propiedad 2. Aditividad
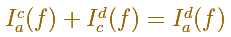
También define
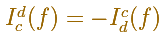
Después prueba que existe una manera de asignar estos números (la integral) y que esta asignación es única. Habitualmente se denota por
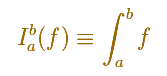
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES