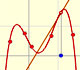
Polynomios de Taylor: función racional 1
La función racional
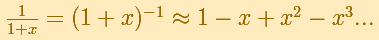
es, al igual que el ejemplo de la raíz cuadrada, un caso especial del Teorema del Binomio de Newton. Podemos calcular su serie de Taylor en x = 0 sencillamente.
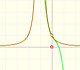
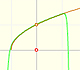
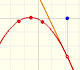
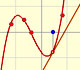
Esta función tiene una singularidad en el punto x = -1. La aproximación es buena entre -1 y +1. Una vez más encontramos una aproximación útil que está centrada en el origen.
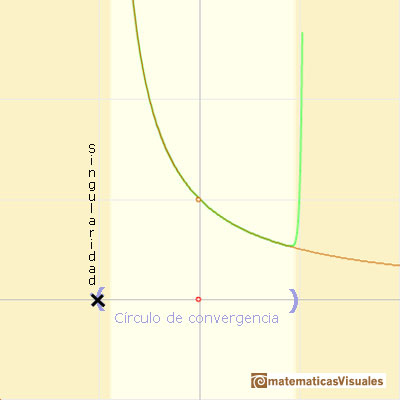
En el punto x = +1 sus ordenadas son alternativamente iguales a 1 y a 0, mientras que la curva original tiene un valor de 1/2.
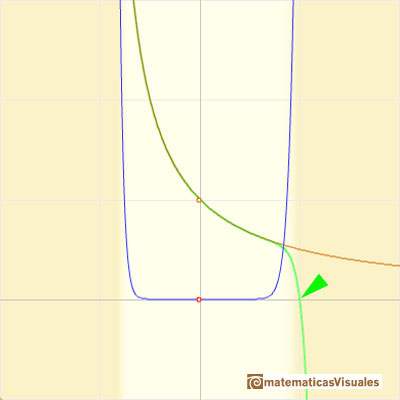
Podemos comparar este comportamiento con el otra función racional: Polinomios de Taylor (5): función racional 2.
REFERENCIAS
Felix Klein - Elementary Mathematics from an Advanced Standpoint. Arithmetic, Algebra, Analysis (pags. 223-228) - Dover Publications
SIGUIENTE
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
ANTERIOR
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
MÁS ENLACES
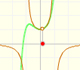
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
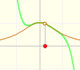
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.
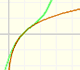
Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.
Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.
Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
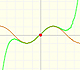
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.