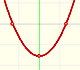
Una función cuadrática es una función polinómica de grado 2 y su representación gráfica es una curva cónica, una parábola.
Estamos interesados en estudiar la derivada de funciones simples con un punto de vista intuitivo y visual. Para estudiar la derivada de una función cuadrática vamos a seguir la misma aproximación que hemos usado para el caso de las funciones afines.
La gráfica de los polinomios de grado menor que 2 son rectas. Podemos decir que las funciones cuadráticas son las más simples de las que se representan por curvas. Son un excelente banco de trabajo para explorar el sentido del concepto de derivada.
Utilizamos funciones cuadráticas para modelar el movimiento uniformemente acelerado, por ejemplo, el movimiento de un cuerpo que cae libremente atraído por la gravedad o la trayectoria de un cuerpo lanzado o disparado, como un balón, una bala o un chorro de agua. En estos modelos no se considera el rozamiento.

La velocidad instantánea de un cuerpo en caída libre es un buen ejemplo de lo que llamamos derivada.
EL CONCEPTO DE DERIVADA DE UNA FUNCIÓN
La derivada de una función en un punto puede definirse como la tasa de variación instantánea o como la pendiente de la recta tangente a la gráfica de la función en ese punto. Podemos definir la pendiente de la función en un punto como la pendiente de la recta tangente.
La pendiente de la tangente depende, en general, de x. Entonces, a partir de una función podemos definir una nueva función, la función derivada de la función original.
El proceso de encontrar la función derivada de una función se llama diferenciación.
El valor de la función dericada para cada valor de x es la pendiente de la función original en x.
Si queremos calcular la derivada de una función en un punto (para un determinado valor de x) podríamos plantearnos dibujar la recta tangente a la gráfica de la función en ese punto y calcular su pendiente. Este es un procedimiento que solo podemos hacer muy aproximadamente.
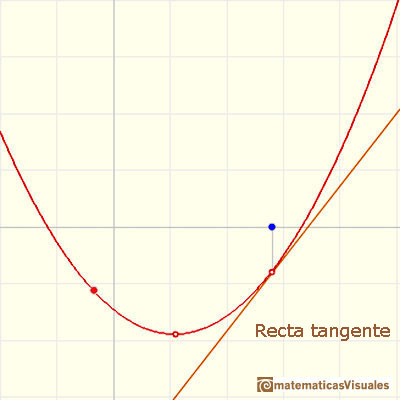
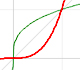
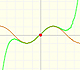
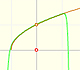
Pero, ¿cómo podemos mejorar la precisión del dibujo de la tangente? Podemos usar una lupa. Si miramos muy cerca del punto de tangencia podemos ver cómo la recta tangente se asemeja a la parábola. La recta tangente es la mejor aproximación lineal de la parábola en ese punto:
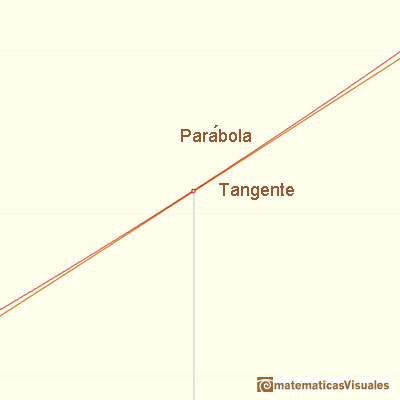
Esta idea de usar una lupa (una lupa de 'infinitos aumentos' sería lo ideal) es una aproximación intuitiva del concepto de límite que es lo que está en la base de la derivada.
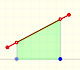
Una vez trazada una buena aproximación de la recta tangente tenemos que calcular su pendiente.
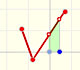
Una manera de hacerlo es dibujar una recta paralela a la tangente pasando por el valor x - 1 y obtenemos un triángulo rectángulo. La longitud del lado vertical es la pendiente de la tangente.
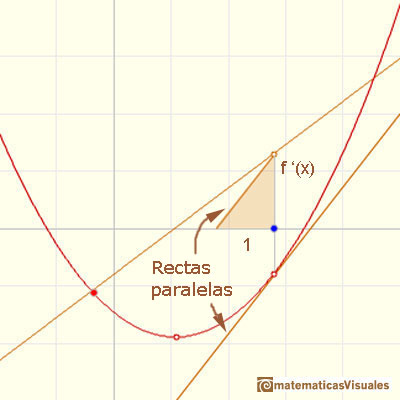
Si hiciéramos este laborioso proceso muchas veces veríamos que esas pendientes parece que están alineadas.
Realmente, las derivadas de una función cuadrática en cada uno de los valores x se representan en una recta.
Como podemos concebir que sabemos calcular la derivada de una función quadrática en cada uno de los valores de x nos planteamos la idea de función derivada. Esta función derivada nos dará el valor de la derivada en cada uno de los valores de x.
Cuando aprendemos a derivar este es uno de los primeros ejemplos que estudiamos.
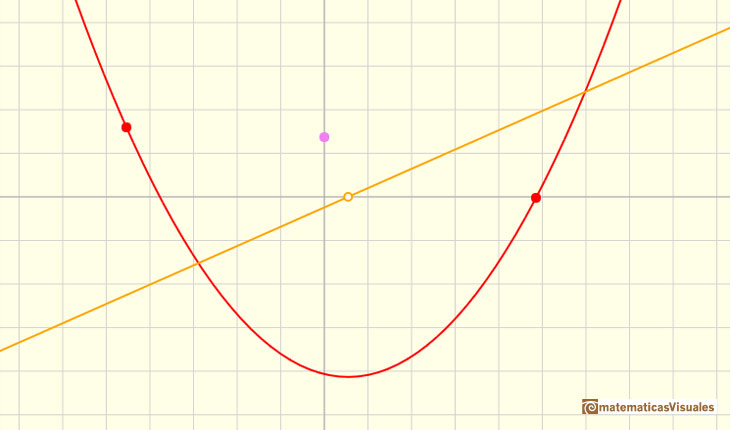
La derivada de una función cuadrática es una función afín:
Vamos a ver cómo la derivada nos va a ayudar a conocer algunas propiedades de la función cuadrática original.
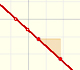
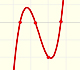
La gráfica de la función derivada es una recta. Además es una recta que no es horizontal, se trata de una recta oblicua.
Nos vamos a fijar en dos propiedades muy sencillas de estas rectas que van a ser interesantes para el estudio de la parábola:
- En ocasiones la recta sube y, otras veces, baja.
- La recta siempre corta al eje de las x.
INVESTIGA
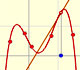
Marca la casilla 'Deriv' y modifica los puntos rojos que determinan la parábola. Al cambiar la función cuadrática la recta va cambiando también. Unas veces va hacia arriba y otras veces hacia abajo.
¿Qué podemos decir de la función cuadrática cuando la recta va hacia arriba o hacia abajo?
Sabemos que la gráfica de una función cuadrática tiene forma de 'montaña' o de 'valle'. Para algunos valores de x estamos en una 'subida' o en una 'bajada'. Decimos que la función crece o decrece. La derivada nos va a decir en qué valores la función crece o decrece. Esto es el estudio del crecimiento-decrecimiento de la función.
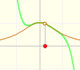
Si nos fijamos en la pendiente de las tangentes, unas veces es positiva (y la función crece) y otras veces es negativa (y la función decrece)
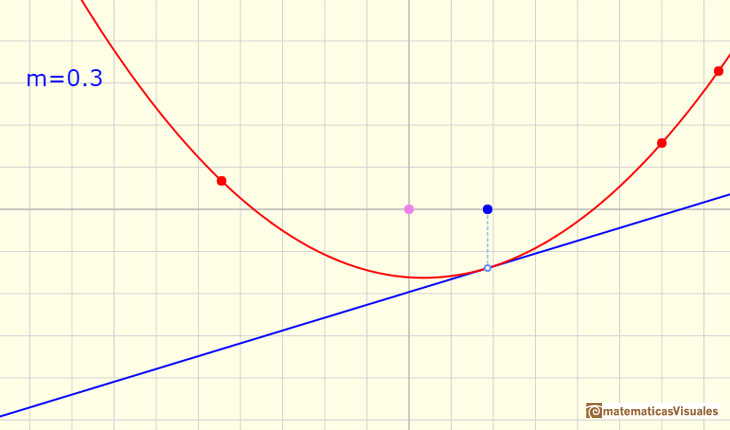
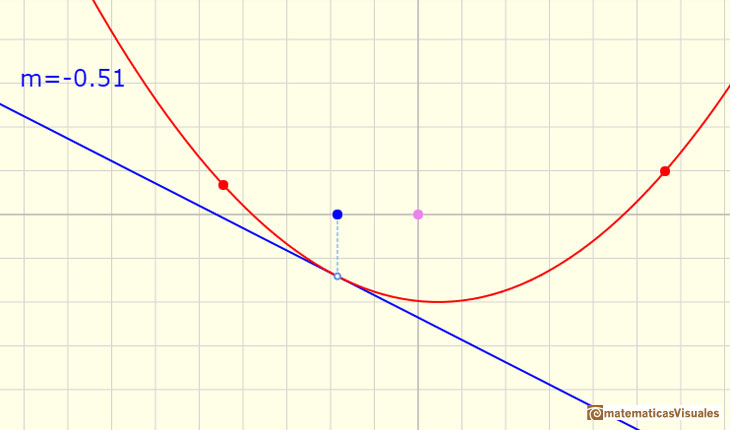
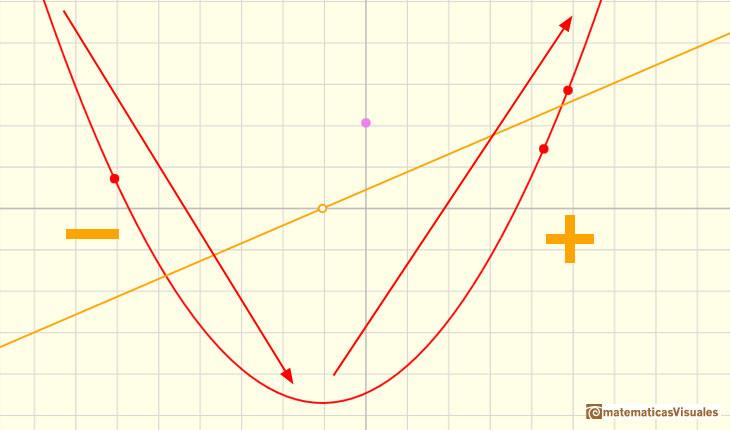
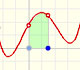
Si ahora nos fijamos en la función derivada vemos la correspondencia entre los valores en los que la recta toma valores negativos y cuando la parábola es decreciente y, al revés, cuando la recta toma valores positivos y la parábola es creciente.
El valor que separa estas dos zonas es, claro está, el punto en el que la recta corta al eje de las x.
Y este valor se corresponde con la 'cumbre de la montaña' o el 'fondo del valle', es decir, con el máximo o el mínimo de la función cuadrática. A este punto lo hemos llamado vértice de la parábola.
INVESTIGA
Enuncia el criterio que podemos seguir para determinar el crecimiento y decrecimiento de una función cuadrática usando la función derivada.
Realmente, con lo que sabemos de las funciones cuadráticas, no haría falta la derivada para determinar el crecimiento y el decrecimiento ni la determinación de su máximo o mínimo.
¿Sabrías determinar el crecimiento y decrecimiento de una función cuadrática sin usar derivadas?
Sin embargo, el criterio de la derivada es lo que utilizamos para determinar el crecimiento y decrecimiento en casos más generales.
Vamos a intentar determinar el vértice de la parábola (que sabemos que es el máximo o el mínimo de la función) y su relación con la derivada.
Ya sabemos calcular con exactitud las coordenadas de este vértice pero estas reflexiones nos servirán para casos más generales.
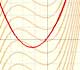
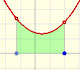
Si quisiéramos calcular el vértice de la parábola 'a ojo' vemos que es difícil hacerlo con precisión. Sin más herramientas no nos atrevemos a dar los valores con una precisión de décimas. Una propiedad muy intuitiva es que la función varía muy poco en torno al máximo o mínimo de la función y por eso nos resulta difícil determinar el punto exacto.
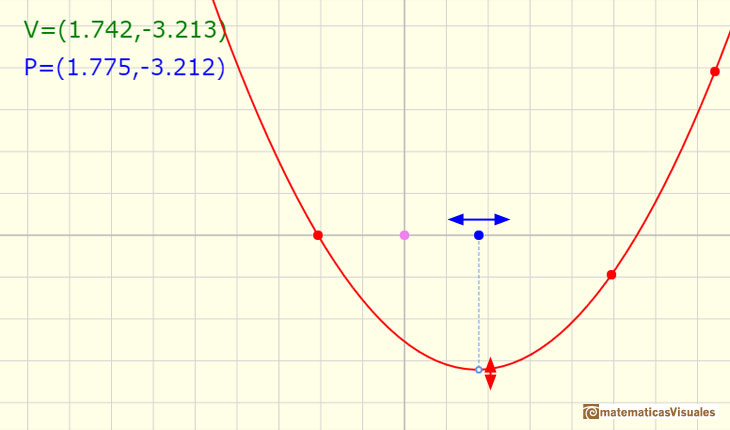
Si suponemos que sabemos dibujar tangentes a la parábola podemos pensar que en el máximo o mínimo la tangente será horizontal, es decir, que su pendiente es 0. Por su interés histórico podemos decir que Pierre Fermat ya sabía que en un máximo o mínimo local la tangente es horizontal
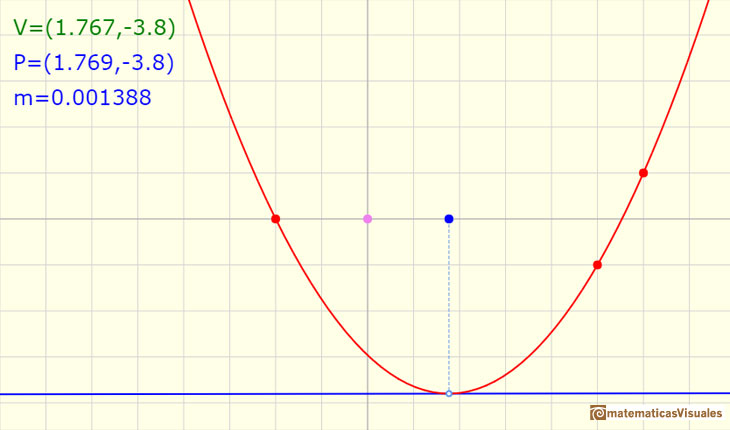
Podemos usar la tangente como un nivel que nos va ayudaría a determinar el máximo o mínimo. Incluso con esta herramienta la determinación 'a ojo' de un máximo o mínimo no se hace con una precisión de milésimas.
INVESTIGA
Marca la casilla "Tangen" y experimenta las dificultades para determinar el máximo o mínimo de una parábola con la máxima precisión.
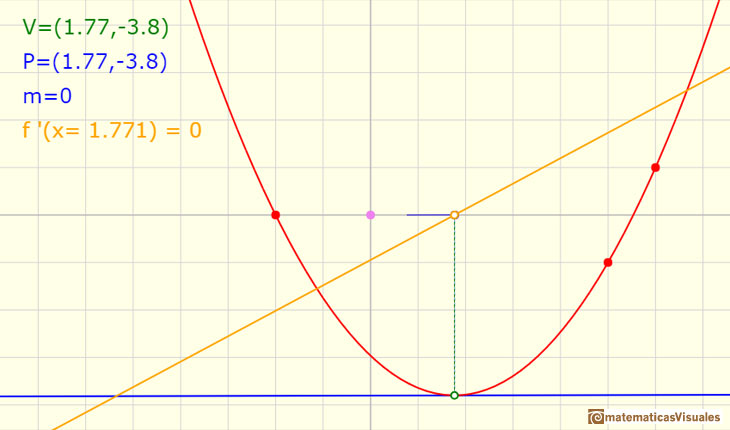
La derivada es la herramienta definitiva para encontrar el máximo o mínimo de una función polinómica.
INVESTIGA
Enuncia el critero para determinar los máximos o mínimos de una función usando derivadas, es decir, relacionándolo con el corte de la función derivada con el eje de las x.
Comprueba que con este procedimiento calculamos el vértice de la parábola.
Los valores en los que la derivada de una función polinómica vale 0 se llaman valores críticos de la función.
Estos valores críticos nos permiten calcular los máximos y mínimos (relativos) de las funciones polinómicas. Veremos cuando estudiemos las funciones cúbicas que puede darse el caso de que en un valor crítico no tengamos un máximo ni un mínimo.
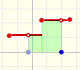
Una idea simple e interesante es que cuando trasladamos arriba y abajo el gráfico de la función (sumamos o restamos un número a la función original) la función derivada no cambia. La razón es muy intuitiva. Cuando movemos el punto violeta trasladamos verticalmente la función y la función derivada no cambia:
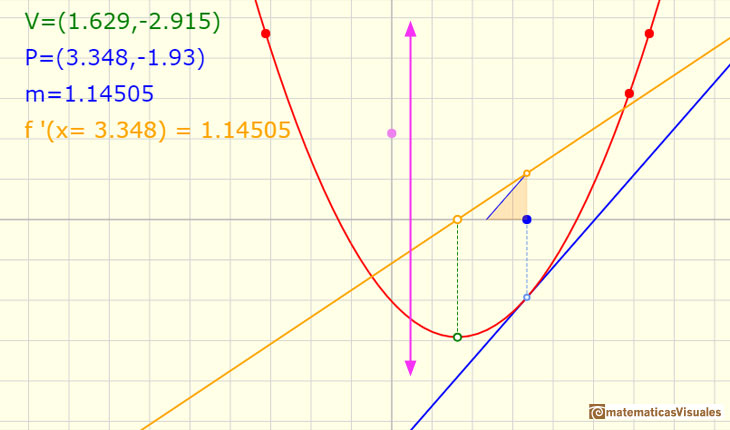
Es importante notar que la derivada de un polinomio de grado 1 es una función constante (un polinomio de grado 0). Y que la derivada de un polinomio de grado 2 es un polinomio de grado 1.
Cuando derivamos esas funciones polinómicas el resultado es un polinomio de un grado menor que la función original.
Cuando estudiamos la integral de un polinomio de grado 2 veremos que en este caso la nueva función es un polinomio de grado 3. Un grado más que la función original.
Estos resultados están relacionados con el Teorema Fundamental del Cálculo.
REFERENCIAS
 ANTERIOR
ANTERIOR
MÁS ENLACES























 SIGUIENTE
SIGUIENTE